ЗАДАЧИ 11
Учеб. пособие Г&Щ, ч.2, стр. 70 – 110.
Примеры решения задач.
1.
Передаточная функция фильтра имеет вид 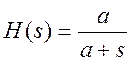 . Найдите частоту среза фильтра по
уровню 3 дБ.
. Найдите частоту среза фильтра по
уровню 3 дБ.
Решение.
Частотная характеристика фильтра 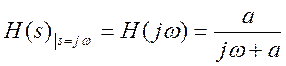 . АЧХ
фильтра
. АЧХ
фильтра 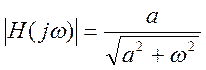 . При этом
. При этом ![]() и
и
![]() - монотонно убывающая функция ω. Для
частоты среза
- монотонно убывающая функция ω. Для
частоты среза 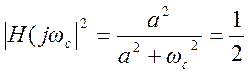 . Отсюда
. Отсюда ![]() .
.
2.
Задана передаточная функция фильтра 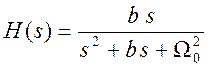 .
Определите тип фильтра, постройте график АЧХ.
.
Определите тип фильтра, постройте график АЧХ.
Решение.
Частотная характеристика фильтра 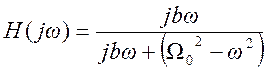 .
Следовательно, квадрат АЧХ фильтра
.
Следовательно, квадрат АЧХ фильтра 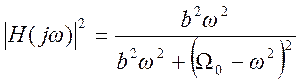 . Значения АЧХ
для характерных частот
. Значения АЧХ
для характерных частот ![]() . Поэтому фильтр
– полосовой. График АЧХ фильтра для
. Поэтому фильтр
– полосовой. График АЧХ фильтра для ![]()
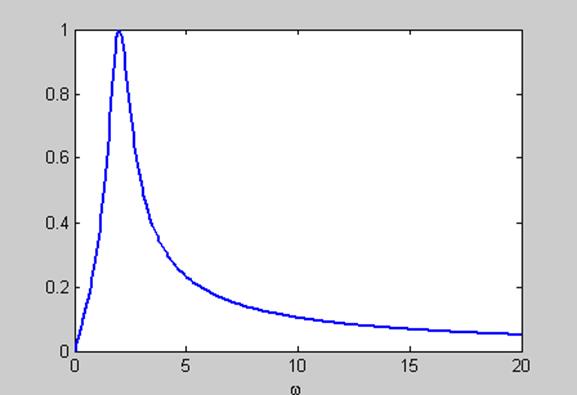
Рис.11.1.
3.
Используя частотное преобразование, определите передаточную функцию ФВЧ
Баттерворта 2 –го порядка с частотой среза 2 Гц.
Решение.
Запишем передаточную функцию нормированного ФНЧ Баттерворта
2 – го порядка 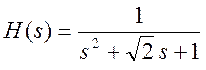 . График АЧХ такого
фильтра
. График АЧХ такого
фильтра
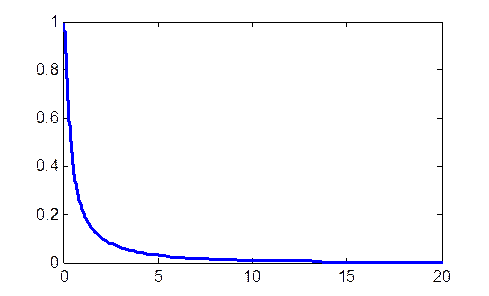
Рис. 11.2
Угловая частота среза целевого ФВЧ ![]() .
Выполняя подстановку
.
Выполняя подстановку 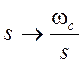 и последующие преобразования,
получим передаточную функцию ФВЧ в виде
и последующие преобразования,
получим передаточную функцию ФВЧ в виде
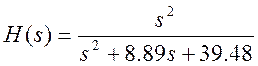 .
.
График АЧХ целевого фильтра
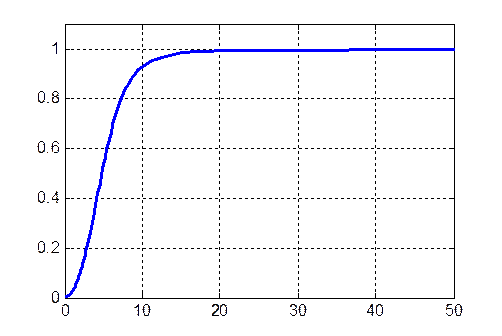
Рис. 11.3
4.
Определите импульсную характеристику (ИХ) и тип цифрового фильтра с
уравнением ![]() .
.
Решение. Для получения ИХ фильтра подадим на его вход единичный импульс
![]() . Тогда значения импульсной
характеристики
. Тогда значения импульсной
характеристики
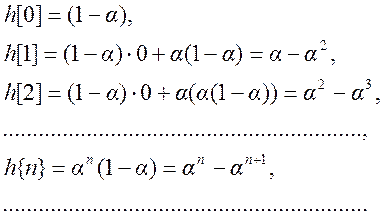
Для α < 1 значения импульсной характеристики убывают в геометрической
прогрессии.
Передаточная функция фильтра 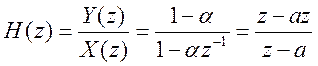 .
.
Частотная характеристика
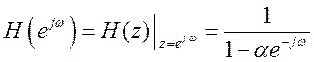 . АЧХ фильтра
. АЧХ фильтра 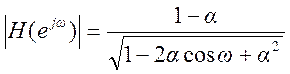 .
.
При возрастании ω знаменатель АЧХ увеличивается, а сами значения уменьшаются. График АЧХ для значения α = 0,8. Тип фильтра - ФНЧ.
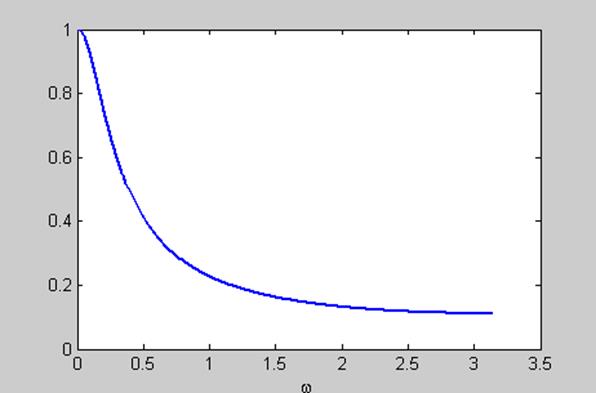
Рис. 11.4
5.
Определите тип фильтра с уравнением ![]() .
Найдите амплитуду выходного сигнала фильтра для входного сигнала
.
Найдите амплитуду выходного сигнала фильтра для входного сигнала ![]() .
.
Решение.
Частотная характеристика фильтра ![]() . График АЧХ
фильтра для
. График АЧХ
фильтра для ![]()
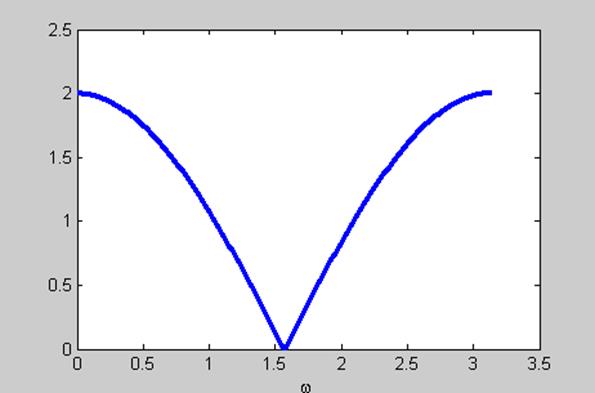
Рис. 115
Тип фильтра – режекторный.
Амплитуда выходного сигнала при ![]()
Если ![]() , то выход системы
, то выход системы ![]() . Поэтому в данном случае
. Поэтому в данном случае ![]() .
.
6. Определите тип фильтра и найдите его частоту среза на уровне 3 дБ.
Передаточная функция фильтра
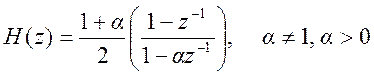 .
.
Решение.
ЧХ фильтра
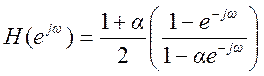 . Его АЧХ
. Его АЧХ 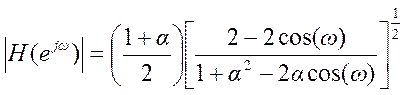 .
.
Для ![]() ,
для
,
для ![]() , поэтому тип фильтра –ФВЧ.
, поэтому тип фильтра –ФВЧ.
Вид АЧХ для ![]() ,
,
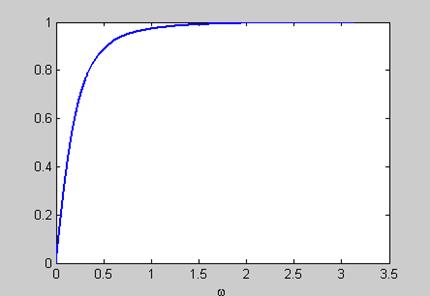
Рис. 11.6
Частоту среза определим из
условия 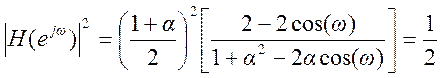 .
.
Отсюда после преобразований получаем ![]() . Или
. Или 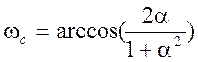 .
.
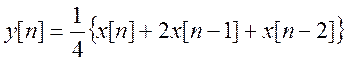 .
.Для определения импульсной характеристики (ИХ) достаточно подать на вход фильтра единичны импульс, следовательно, импульсная характеристика
![]() .
.
Передаточная функция фильтра – это Z – преобразование ИХ, поэтому
![]() .
Такая передаточная функция имеет двойной нуль при z =
-1. Частотная характеристика фильтра
.
Такая передаточная функция имеет двойной нуль при z =
-1. Частотная характеристика фильтра ![]() .
На рис. 11.7 показаны АЧХ и ФЧХ фильтра
.
На рис. 11.7 показаны АЧХ и ФЧХ фильтра
для частоты дискретизации FS = 500 Гц.
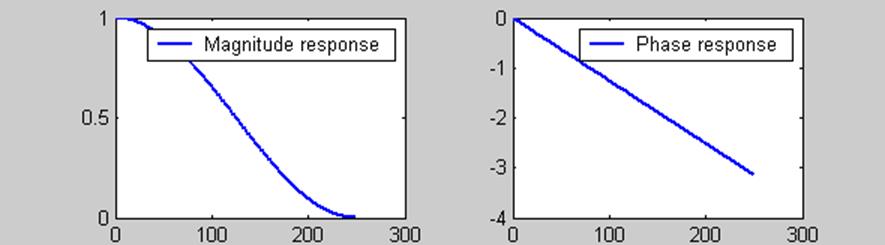
Рис. 11.7
Следовательно, данный простой КИХ - фильтр может использоваться как ФНЧ для фильтрации высокочастотных помех и шумов.
8.
Рассчитайте цифровой режекторный фильтр, используя метод размещения
нулей и полюсов фильтра на комплексной плоскости. Спецификация фильтра:
- частота режекции 50 Гц,
- ширина полосы режекции на уровне 3 дБ ![]() Гц
Гц
- частота дискретизации 500 Гц.
Решение.
Для обеспечения режекции на частоте 50 Гц при частоте дискретизации 500 Гц поместим
пару комплексных нулей в точках единичной окружности с угловыми координатами ![]() (рис. 11.8)
(рис. 11.8)
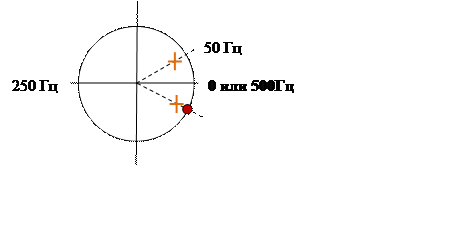 |
Рис. 11.8.
Для получения узкополосного
режекторного фильтра поместим на тех же лучах углов пару дополнительных
комплексно-сопряженных полюсов с модулем (радиусом) ![]() .
От этого параметра зависит ширина полосы режекции фильтра.
.
От этого параметра зависит ширина полосы режекции фильтра.
После определения положения нулей и полюсов фильтра находим его передаточную функцию

По передаточной функции записываем уравнение фильтра
![]() .
.
На рис. 11.9 показана АЧХ спроектированного фильтра
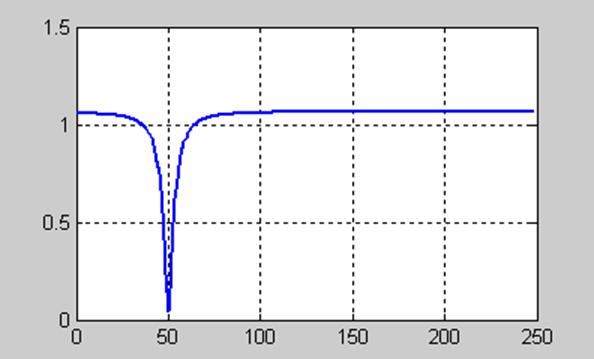
Рис. 11.9
9. Используя
метод инвариантного преобразования импульсной характеристики, рассчитайте
цифровой фильтр Баттерворта второго порядка с частотой среза 200 Гц и частотой
дискретизации 1 кГц.
Решение.
Синтез целевого фильтра выполним на основе расчета аналогового прототипа и его дискретизации, т.е. перехода к цифровому фильтру с помощью метод инвариантного преобразования импульсной характеристики.
Передаточная функция фильтра Баттерворта N – го порядка, выраженная через полюса, имеет вид
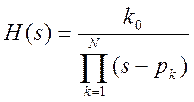
Полюса фильтра с частотой среза ωС определяются по выражению
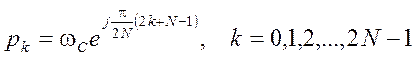 ,
ωС – угловая частота среза в рад/с.
,
ωС – угловая частота среза в рад/с.
Для фильтра второго порядка имеем четыре полюса, из них два полюса в левой полуплоскости, которые и используем для получения передаточной функции фильтра
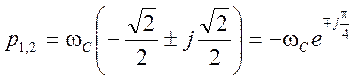 .
.
Отсюда передаточная функция аналогового прототипа
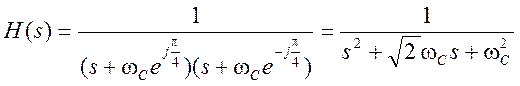 .
.
На рис. 11.10 приведена АЧХ аналогового прототипа фильтра
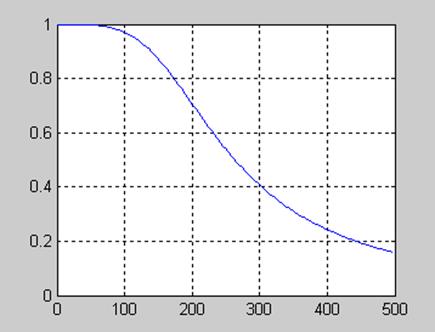
Рис. 11.10.
Для перехода к цифровому фильтру по условию задачи используем метод инвариантного преобразования импульсной характеристики, при котором в качестве его импульсной характеристики берутся отсчеты импульсной характеристики аналогового прототипа.
При этом методе передаточная
функция аналогового фильтра записывается в виде суммы простых дробей 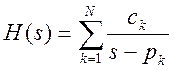 .
.
Для данного случая
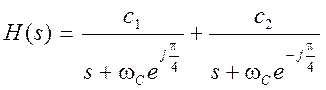 .
Находим константы разложения на простые дроби
.
Находим константы разложения на простые дроби
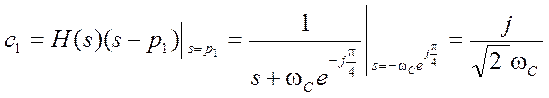 ,
,
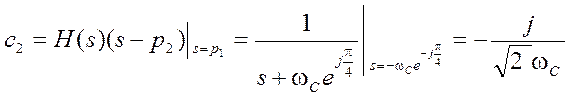 .
.
Таким образом,
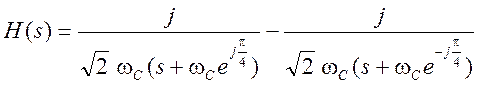 .
.
Передаточная функция цифрового фильтра при данном методе дискретизации аналогового фильтра представляется
как 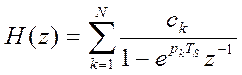 ,
где TS - интервал дискретизации (отсчетов).
,
где TS - интервал дискретизации (отсчетов).
В данном примере TS = 0.001 с и передаточная функция ЦФ
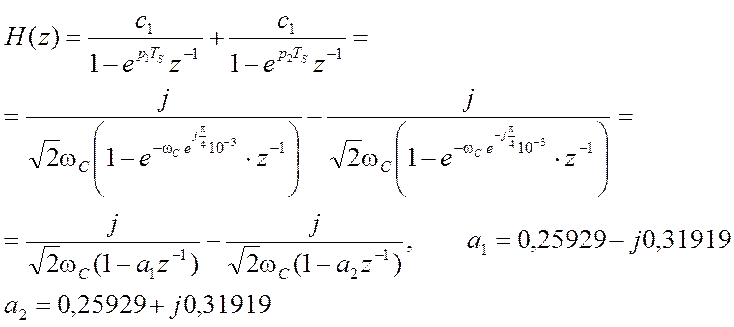
После преобразования
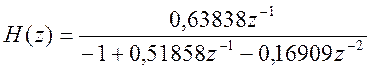 .
.
Передаточная функция цифрового
фильтра получена, из нее подстановкой ![]() может
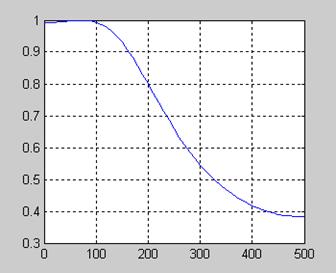
быть найдена частотная характеристика фильтра. На рис. 1111 показана нормированная
АЧХ получившегося фильтра
может
быть найдена частотная характеристика фильтра. На рис. 1111 показана нормированная
АЧХ получившегося фильтра
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.