1. Запись в показательной (полярной) форме комплексного выражения
![]() .
.
![]()
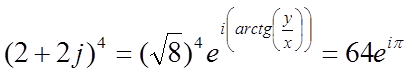
2.
Построение по графику сигнала ![]() путем его
масштабирования и сдвига графика сигнала
путем его
масштабирования и сдвига графика сигнала ![]() .
.
Преобразование сигнала y=sin(t) в сигнал y=4cos2(t+1) осуществляется четырьмя операциями:
1) сдвиг по оси t на ![]() в любую сторону;
в любую сторону;
2) сдвиг влево на 1;
3) сжатие по времени в 2 раза;
4) растяжения вверх
в 4 раза.
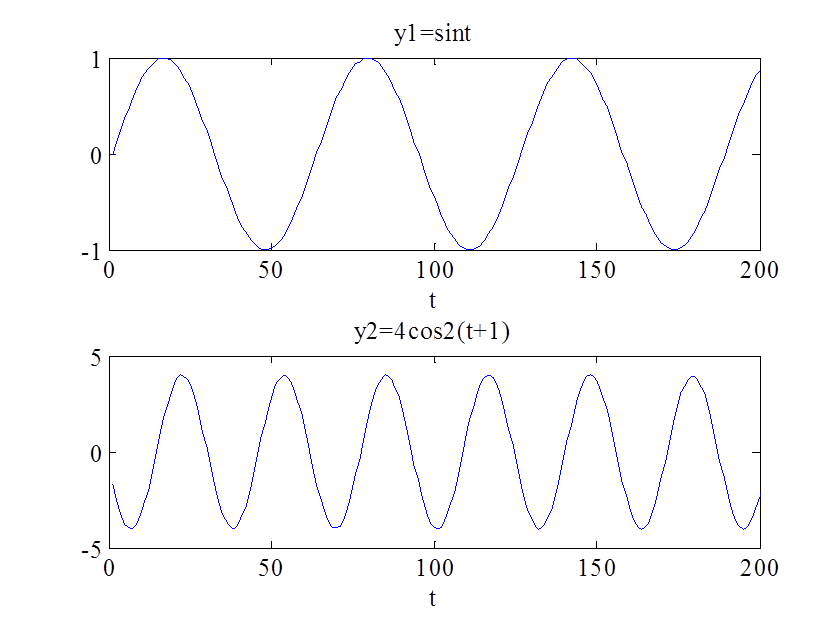
Рис.1. Графики сигналов y1=sin(t) и y2=4cos2(t+1)
3. Определяем для периодического сигнала:
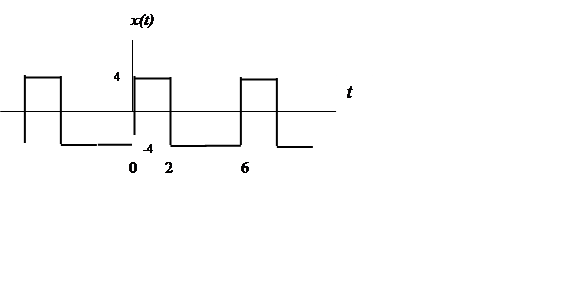
Рис.2. График сигнала из индивидуального задания
а) Максимальное (амплитудное) значение за период равно 4.
б)
Среднее за период значение определяется по формуле ![]() , где T период сигнала,
, где T период сигнала,
равный 6.
![]() .
.
в)
Среднеквадратичное значение определяется по формуле 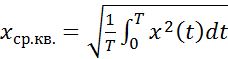
Предварительно можно посчитать интеграл, записанный под знаком корня
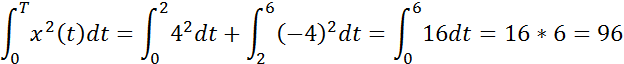
Подстановка получившегося значения в исходную формулу и окончательный расчет
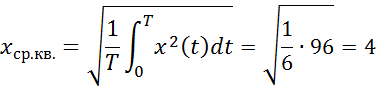
г)
Средняя мощность за период рассчитывается по формуле: ![]() .
.
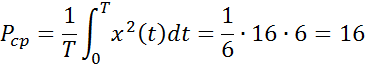
4. Для сигнала из предыдущего пункта (рис.2):
а) Разложение в ряд Фурье
Общий вид комплексного ряда Фурье: ![]() ,
где
,
где ![]() -
это частота основной гармоники, равная
-
это частота основной гармоники, равная ![]() .
.
Определение коэффициентов ряда:
![]()
![]()
![]()
Подстановка получившейся формулы коэффициента ряда в исходную формулу
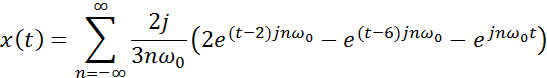
б) Амплитудный и фазовый спектры сигнала.
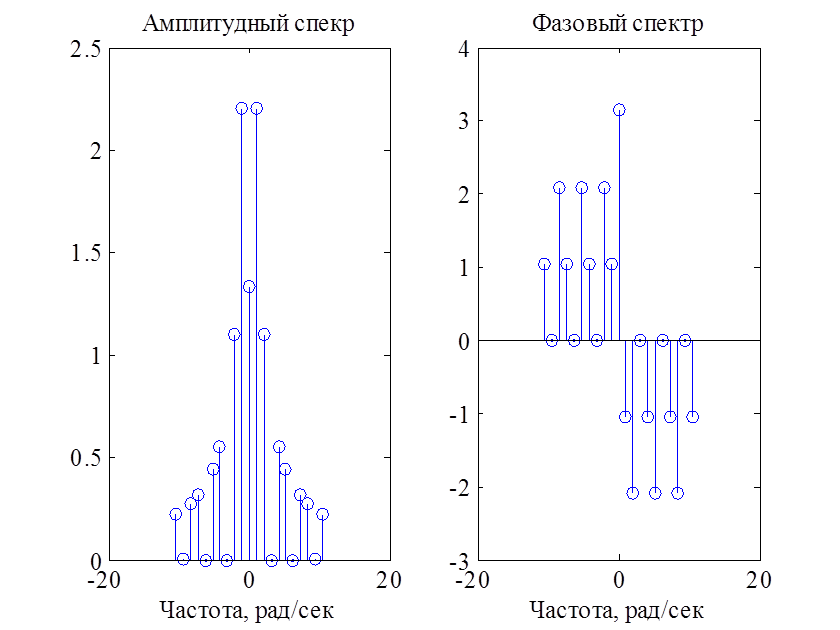
Рис.3. Амплитудный и фазовый спектры сигнала
в) Физический смысл спектров.
Амплитудный спектр выражает
плотность амплитудных гармоник, входящих в непрерывный сигнал. Значение
амплитуды пилообразного периодического сигнала стремится к нулю при ![]()
Фазовый спектр отражает зависимость от частоты начальных фаз гармоник сигнала.
г) Построение графика сигнала для конечного ряда Фурье с числом гармоник k = 5, 10, 20.
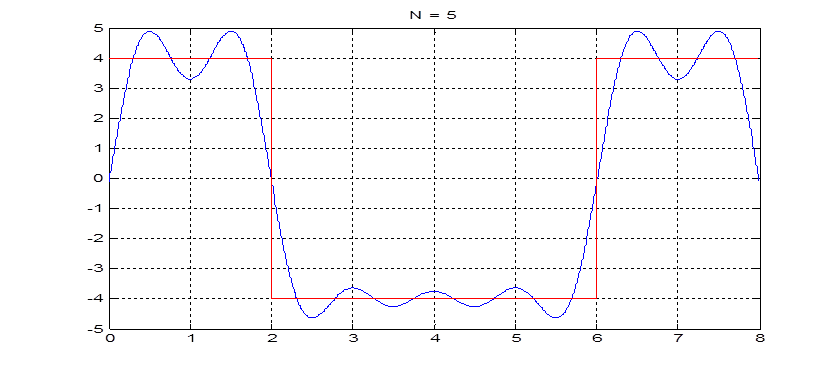
Рис.4. График сигнала и приближение его рядом Фурье при N=5
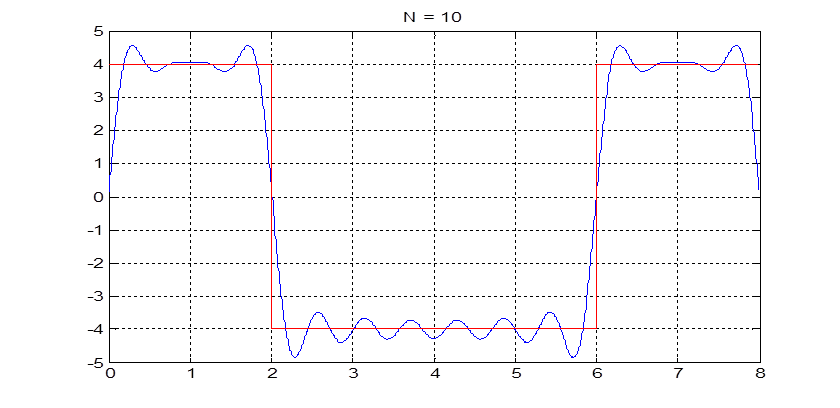
Рис.5. График сигнала и приближение его рядом Фурье при N=10
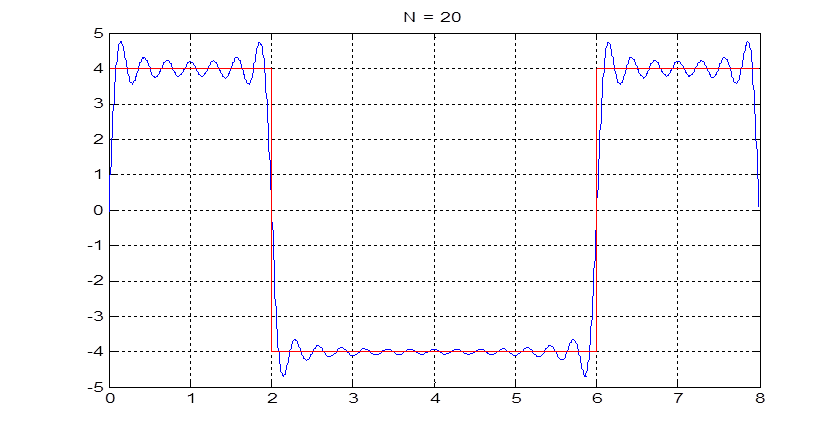
Рис.6. График сигнала и приближение его рядом Фурье при N=20
5. Для сигнала 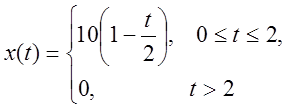
а) найти преобразование Фурье,
б) определить амплитудный и фазовый спектры и постройте их графики,
в) объясните физический смысл спектров.
а) Преобразование Фурье.
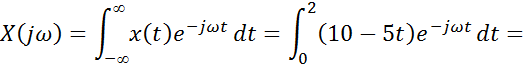
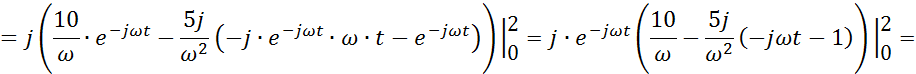
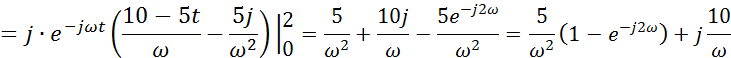
б) Амплитудный и фазовый спектры.
![]() =
=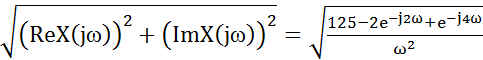
![]() =arctg
=arctg![]() =arctg
=arctg![]()
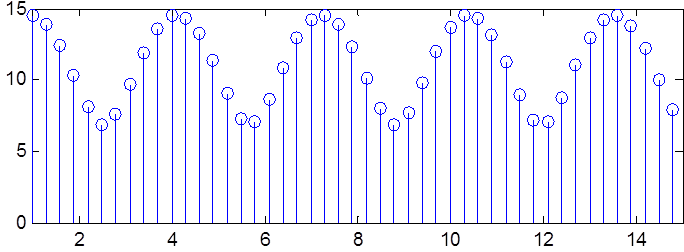 |
Частота, рад/сек
Фазовый спектр
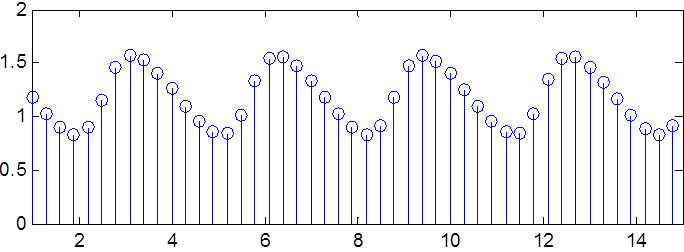 |
Рис.7. Амплитудный и фазовый спектры сигнала
в) Физический смысл спектров.
Обратимся к выражению обратного преобразования Фурье в виде
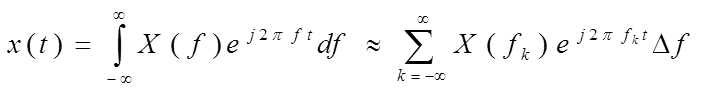 .
.
Амплитудный спектр представляет
собой модуль спектральной плотности сигнала 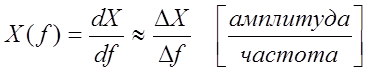 .
.
X(f) имеет смысл плотности амплитуды гармоник, приходящихся на единичный интервал частот вблизи рассматриваемой частоты f. Этим и объясняется название X(f) или X(jω)– спектральная плотность сигнала
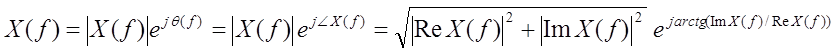 )
)
Фазовый спектр – аргумент спектральной плотности X(f).
Для действительных сигналов амплитудный спектр |X(f)| - четная функция,
фазовый спектр ![]() – нечетная функция f.
– нечетная функция f.
6.
Вычисление дискретной свертки сигнала 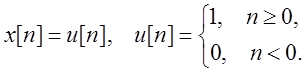
и
сигнала 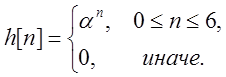
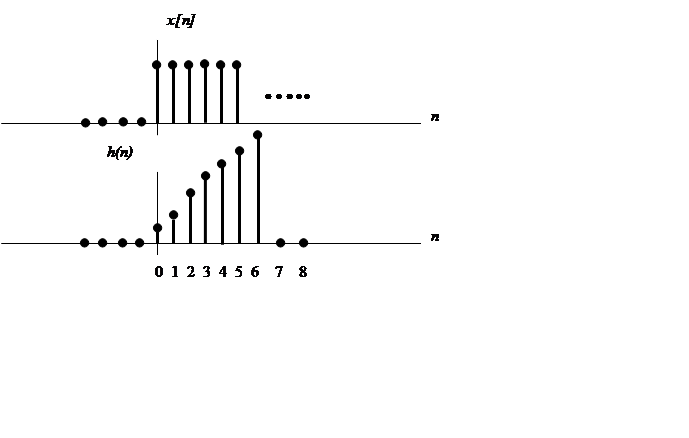 |
Рис.8. Графики сигналов
При n<0 сигналы не перекрываются и свертка равна нулю.
При ![]() перекрываются на промежутке
перекрываются на промежутке
![]() :
:
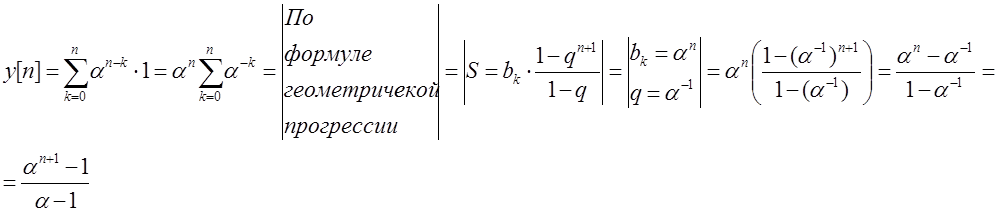
При n>6 перекрываются на
промежутке ![]() :
:
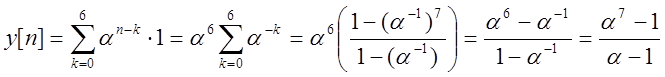
Таким образом 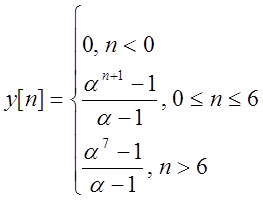
Но так как сигнал h[n] необходимо было реверсировать, этот ответ не совсем верен. При реверсировании сигнала мы получим иной ответ:
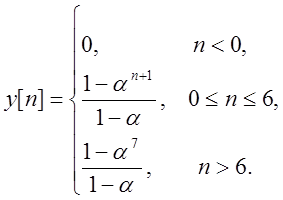
Для построения графика
предположим, что ![]() , тогда:
, тогда:

Рис.9. График свертки
сигналов ![]() и
и 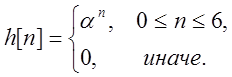
7. Вычисление
дискретного преобразования Фурье (ДПФ) для сигнала ![]() .
.
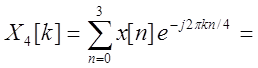
![]() =
=
=1+2![]()
![]()
![]()
![]()
![]()
Дискретное преобразование Фурье:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.