МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
по курсу «Теория и обработка сигналов»
Вариант 3
Группа: АТ-73 Преподаватель: доц. Щетинин Ю.И.
Студент: Кухарева А.В.
Новосибирск
2009
1. Представление комплексного числа в полярной форме.
Запишем комплексное число ![]() в показательной (полярной) форме,
воспользовавшись выражением (1).
в показательной (полярной) форме,
воспользовавшись выражением (1).
![]() (1)
(1)
![]()
2. Построение графика сигнала путём масштабирования и сдвига.
По графику сигнала ![]() путем его масштабирования и сдвига
построим график сигнала
путем его масштабирования и сдвига
построим график сигнала ![]() .
.
Для этого увеличим амплитуду сигнала
![]() в 2 раза и сдвинем его на 1 отсчёт
влево вдоль оси Ot .
в 2 раза и сдвинем его на 1 отсчёт
влево вдоль оси Ot .
С помощью следующей
последовательности команд построим график сигнала ![]() и сдвинутого
сигнала
и сдвинутого
сигнала ![]() .
.
t = -8:0.01:8;
y = 2*sin(t+1);
y1 = sin(t);
plot(t,y,t,y1), grid
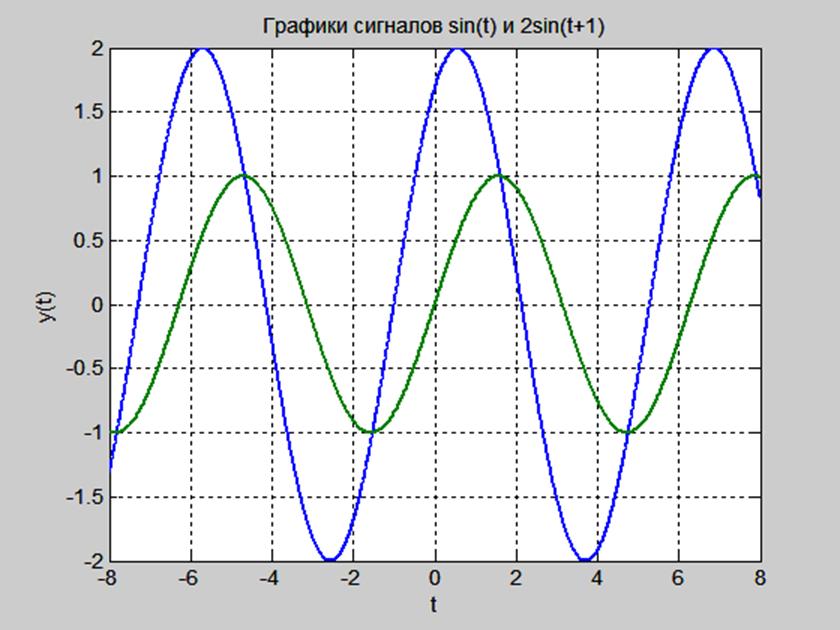
Рис. 1. График сигнала ![]() и сдвинутого сигнала
и сдвинутого сигнала ![]() .
.
3. Определение характеристик системы.
Дана дискретная во времени система
с уравнением ![]() .
.
Система является линейной, если для неё справедлив принцип суперпозиции:
Если ![]() ,
то
,
то 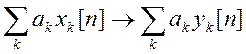
Проверим, линейна ли заданная система.
Пусть при ![]()
![]() и при
и при ![]()
![]() .
.
Если ![]() ,
то
,
то ![]() , значит, система линейна.
, значит, система линейна.
Система является стационарной (инвариантной во времени), если временной сдвиг сигнала на входе вызывает такой же сдвиг сигнала на выходе системы.
Проверим, стационарна ли заданная система.
Если ![]() ,
то
,
то ![]() , значит, система не стационарна.
, значит, система не стационарна.
Система является осуществимой (каузальной), т.к. зависит только от настоящих значений аргумента n, но не от будущих.
Итак, выяснили, что система является линейной, нестационарной и каузальной.
4. Определение характеристик периодического сигнала.
Периодический сигнал x(t) задан графиком, представленным на рис.2.
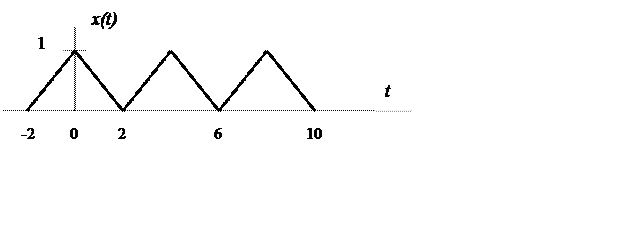
Рис. 2. График периодического сигнала x(t).
Определим характеристики данного сигнала:
а) максимальное за период значение
![]()
б) среднее за период значение
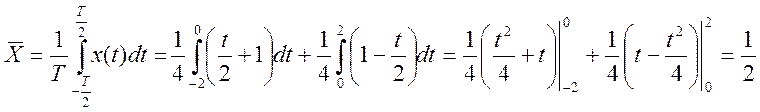 (2)
(2)
в) среднеквадратичное значение
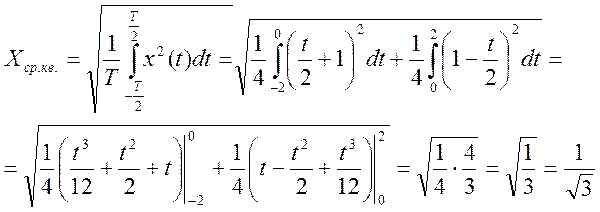 (3)
(3)
г) средняя мощность за период
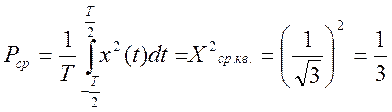 (4)
(4)
5. Разложение периодического сигнала в ряд Фурье и построение его спектров.
Для сигнала x(t) (рис.2) выполним разложение в комплексный ряд Фурье.
Определим коэффициенты ![]() комплексного ряда Фурье по выражению
.
комплексного ряда Фурье по выражению
.
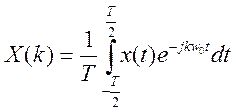 (5)
(5)
Сигнал x(t) периодический с периодом T
= 4 и угловой частотой 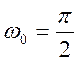 .
.
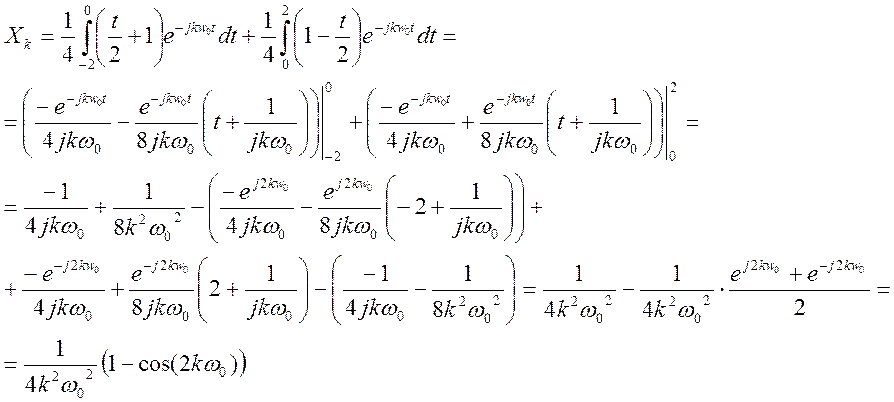
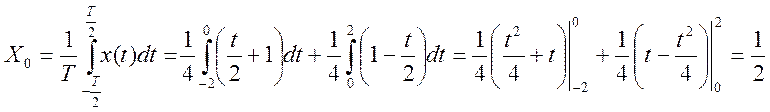
Таким образом, получили 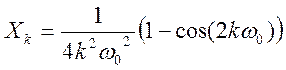 (6)
(6)
и комплексный ряд Фурье можно записать в виде (7).
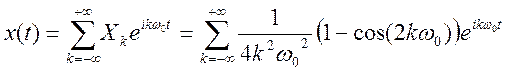 (7)
(7)
Используя выражение (6), построим амплитудный и фазовый спектры сигнала x(t) с помощью следующего script-файла.
omega = pi/2;
N = input('Number of harmonics ');
X0 = 0.5;
k1 = -N:-1;
X1 = (1./(4*(k1.^2)*(omega^2))).*(1-cos(2*k1*omega));
k2 = 1:N;
X2 = (1./(4*(k2.^2)*(omega^2))).*(1-cos(2*k2*omega));
X = [X1 X0 X2];
k = [k1 0 k2];
subplot(2,1,1);
stem(k*omega, abs(X));
title('Амплитудный спектр')
subplot(2,1,2);
stem(k*omega, angle(X));
title('Фазовый спектр')
xlabel('wk')
Полученные результаты представлены на рис.3.
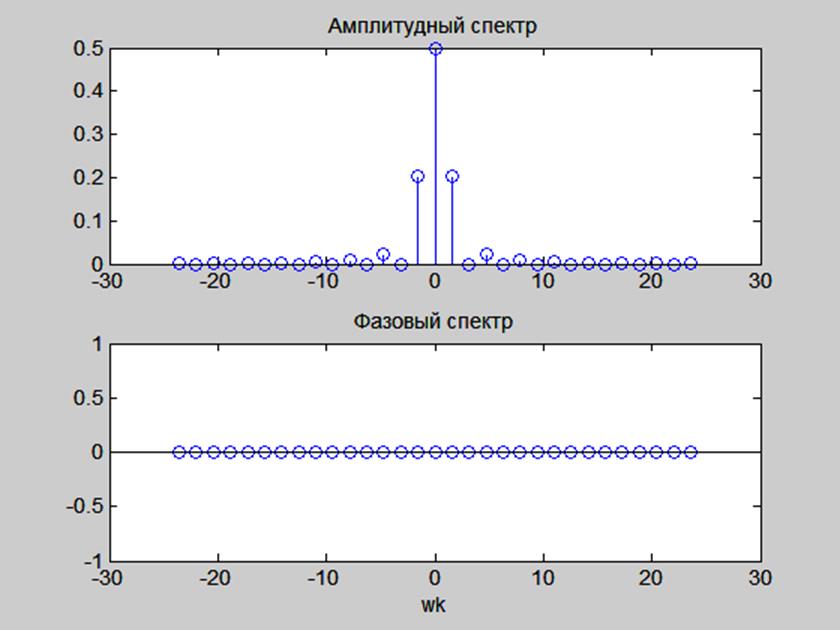
Рис. 3. Амплитудный и фазовый спектры сигнала x(t).
Амплитуды гармоник с возрастанием
номера гармоники уменьшаются как ![]() .
.
Это объясняется тем, что данный сигнал не имеет разрывов.
Сигнал ![]() чётный,
значит, коэффициенты
чётный,
значит, коэффициенты 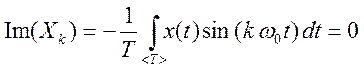 .
.
Следовательно, 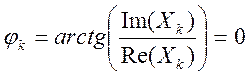 и фазовый спектр сигнала нулевой.
и фазовый спектр сигнала нулевой.
Используя выражение (7) построим графики сигнала и ряда Фурье с числом гармоник
N = 5, 10, 20 с помощью следующего script-файла.
T=4;
w0 = 2*pi/T;
t = -T:T/1000:T; % интервал времени
% исходный сигнал
x1=tripuls(t,4)+tripuls(t-4,4)+tripuls(t+4,4);
N = input('Number of harmonics ');
N = 4;
c0 = 0.5;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
% коэффициенты Фурье
cn = (1./(4*(n.^2)*(w0^2))).*(1-cos(2*n*w0));
c_n = conj(cn);
% Приближение сигнала рядом Фурье
x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);
end
plot(t,x,t,x1, '--r'), grid
title(['N = ',num2str(N)])
Полученные результаты представлены на рис. 4 – 6.
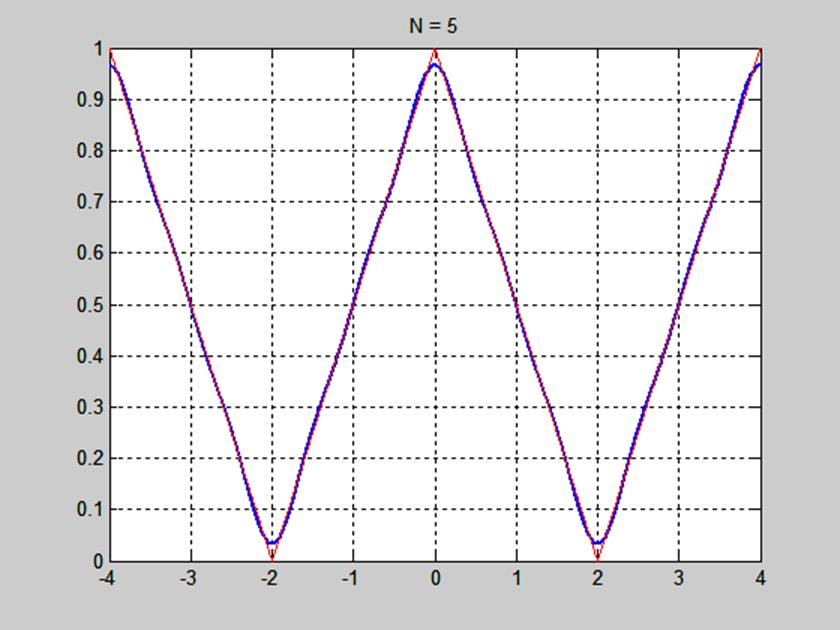
Рис. 4. График сигнала и его приближения рядом Фурье при числе гармоник N=5.
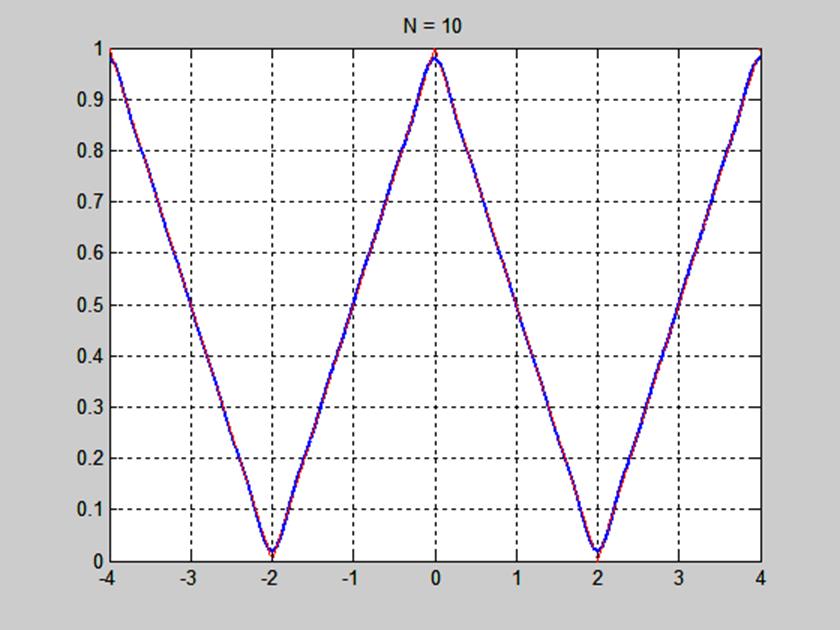
Рис. 5. График сигнала и его приближения рядом Фурье при числе гармоник N=10.
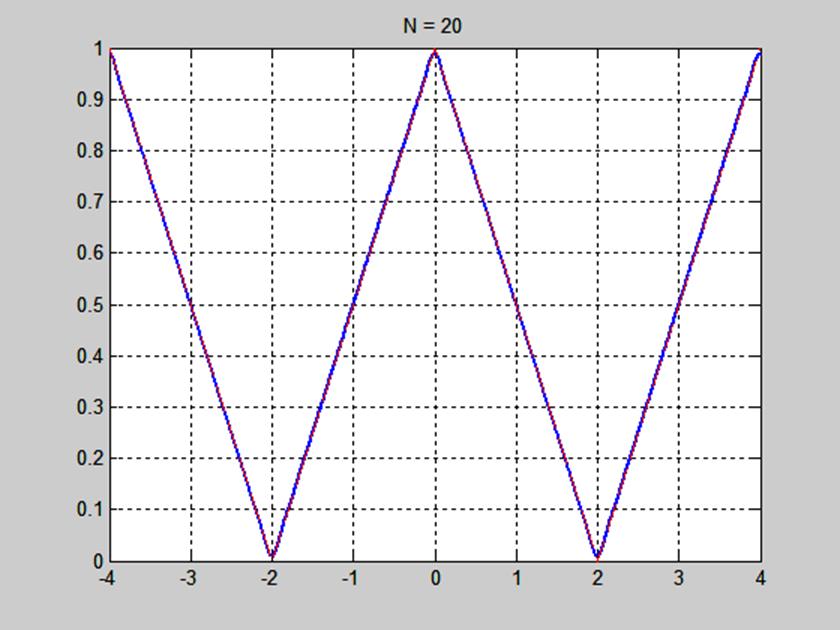
Рис. 6. График сигнала и его приближения рядом Фурье при числе гармоник N=20.
На рис. 4 – 6 видим, что частичные суммы ряда Фурье сходятся к сигналу при числе гармоник N=5, N=10, N=20. Аппроксимация сигнала рядом Фурье тем лучше, чем больше гармоник входит в сумму ряда.
6. Вычисление преобразования Фурье сигнала и построение его спектров.
Дан сигнал ![]()
Для упрощения нахождения преобразования Фурье данного сигнала воспользуемся свойством частотного сдвига преобразования Фурье.
Заданный сигнал ![]() перепишем в виде (8).
перепишем в виде (8).
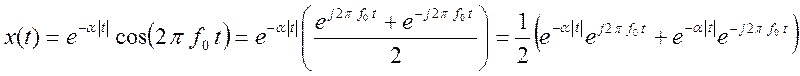 (8)
(8)
Найдём преобразование Фурье
сигнала ![]() по выражению (9).
по выражению (9).
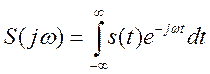 (9)
(9)
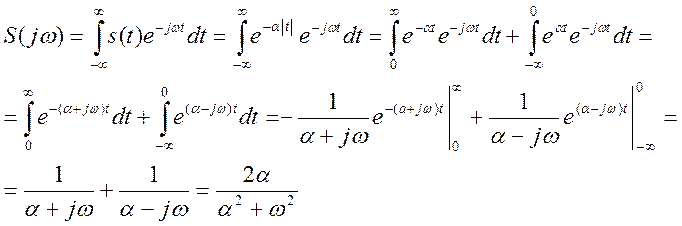
Согласно свойству частотного
сдвига, если ![]() , то
, то 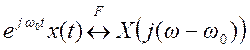 .
.
Таким образом, преобразование
Фурье для сигнала ![]() найдём, как
найдём, как
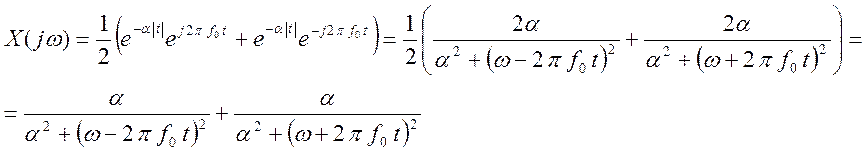
Итак, выражение спектральной
плотности для сигнала ![]() будет иметь вид (10).
будет иметь вид (10).
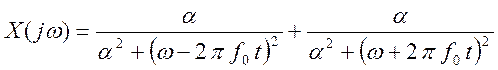 (10)
(10)
С помощью следующего script-файла построим графики сигнала ![]() ,
а также его амплитудного и фазового спектров.
,
а также его амплитудного и фазового спектров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.