Представление комплексного числа в полярной форме. Построение графика сигнала путём масштабирования и сдвига. Определение характеристик системы. Определение характеристик периодического сигнала, страница 2

T=10;

dt=0.09; % задание интервала отсчетов

t=-T:dt:T;   % длительность сигнала

a = 0.2, f0 = 10;

s=(cos(2*pi*f0*t)).*exp(-a*abs(t)); % определение сигнала

df=1/(9*T); Fmax=1/dt; % задание частотной шкалы

f=-Fmax:df:Fmax;

w = 2*pi*f;

S=a./(a^2 + (w-2*pi*f0).^2) + a./(a^2 + (w+2*pi*f0).^2); % выражение комплексного спектра

% построение графиков сигнала и спектров

subplot(311), plot(t,s)

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Cигнал')

subplot(312), plot(f,abs(S))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Амплитудный спектр')

subplot(313), plot(f,angle(S))

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Фазовый спектр')

Полученные результаты представлены на рис. 7.

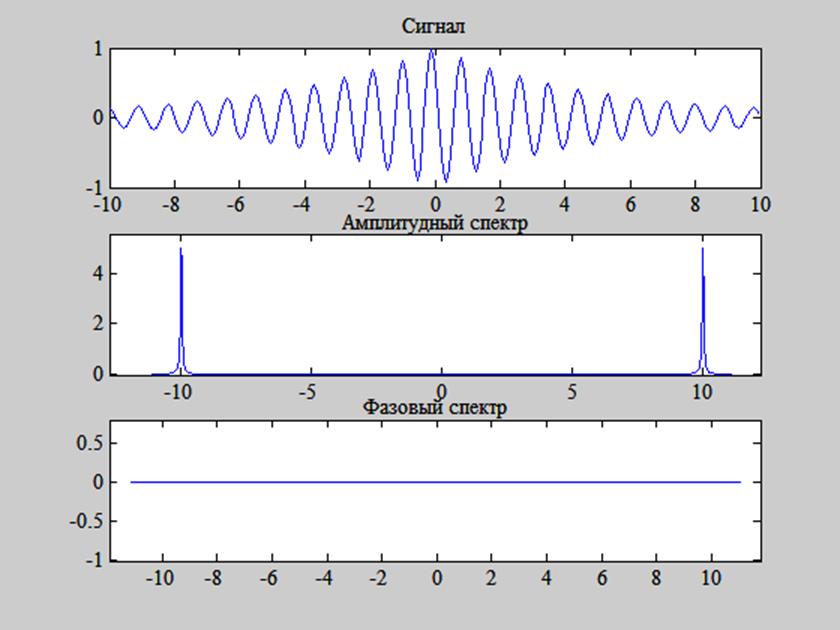
Рис. 7. График сигнала и его амплитудного и фазового спектров.

Фазовый спектр сигнала нулевой, т.к. сигнал чётный и .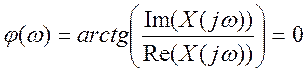

На графике амплитудного спектра сигнала видим пики, которые соответствуют частоте гармоники 10 Гц, входящей в сигнал.

Амплитудный спектр сигнала является суммой спектров сигнала , сдвинутых по частоте.

7.  Вычисление дискретной свёртки сигналов.

Даны сигналы

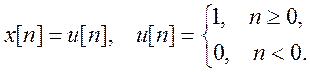     и    .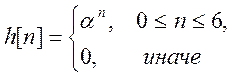

Графики этих сигналов () представлены на рис. 8.

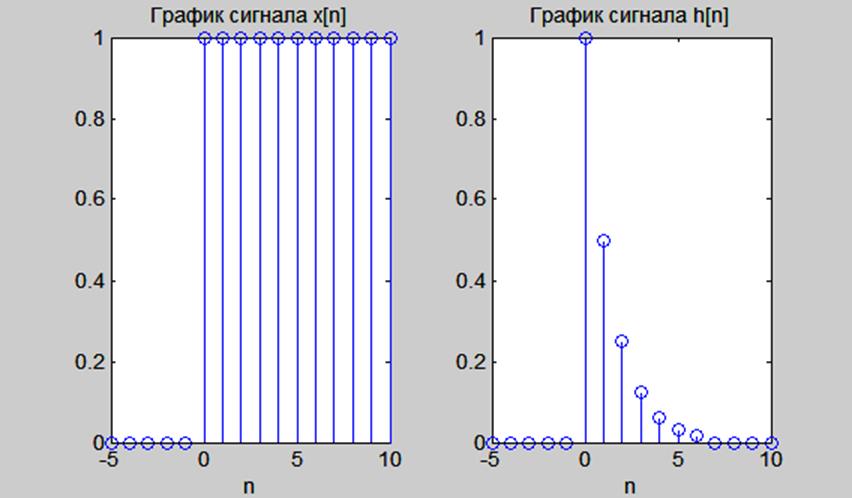
Рис. 8. Графики сигналов x[n],  h[n].

Вычислим дискретную свёртку y[n] этих сигналов по выражению 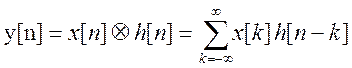(11).

                                                                                              (11)

Зеркально отразим сигнал h[k] относительно начала координат (рис. 9) и будем сдвигать его вправо на n, находя сумму (11).

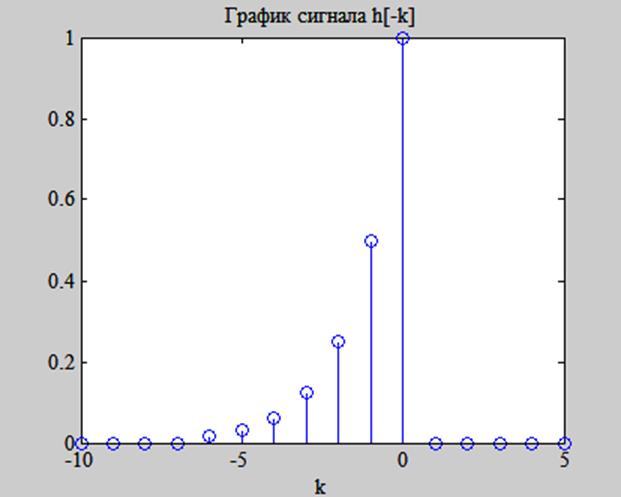
Рис. 9. График сигнала h[k], зеркально отражённого относительно начала координат.

Разобьём ось n на 3 интервала.

1) На интервале n < 0  x[k]  и h[n-k]  не перекрываются, поэтому  y[n]=0.

2) На интервале     при , значит,

 

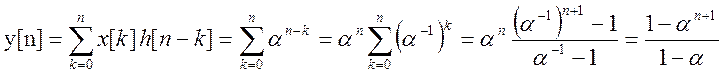
3) На интервале     при , значит,

 

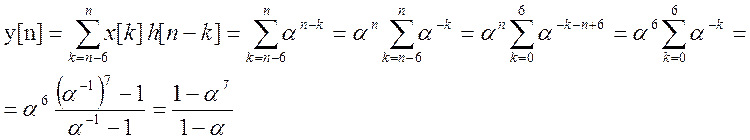
Таким образом, получили свёртку сигналов 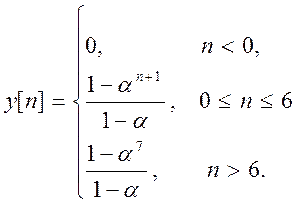(12).

                                                                                (12)

Построим график свёртки сигналов по выражению (12).

Результат представлен на рис. 10.

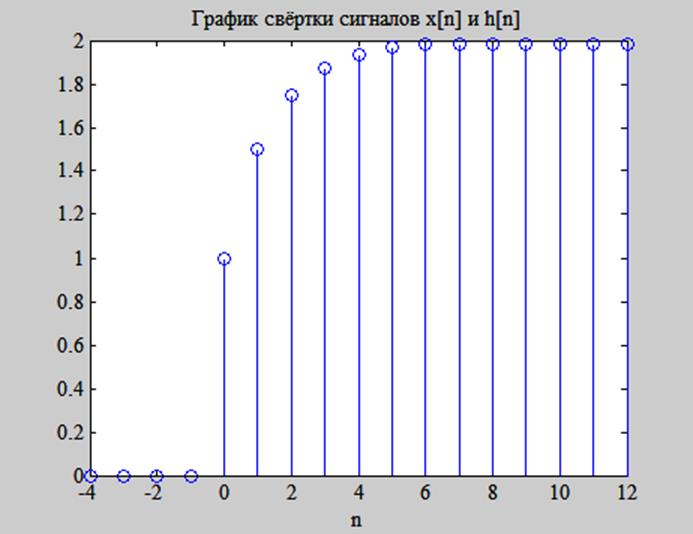
Рис. 10. График свёртки сигналов .

8.  Вычисление дискретного преобразования Фурье сигнала.

Дан сигнал .

Вычислим его ДПФ по выражению (13) для числа размера ДПФ N=6.

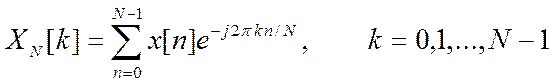,                                                           (13)

где X – N-точечный вектор ДПФ, x – вектор сигнала во временной области.

Размер ДПФ больше числа точек сигнала, поэтому необходимо сигнал дополнить нулями,  т.е.   .        

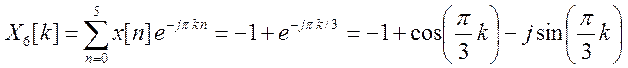
Вычислим 6 членов ряда.

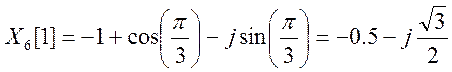
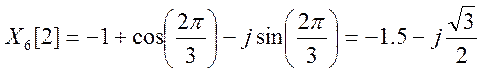
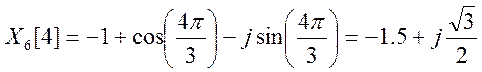
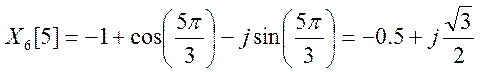
Построим графики амплитудного и фазового спектров заданного сигнала.

Результат представлен на рис. 11.

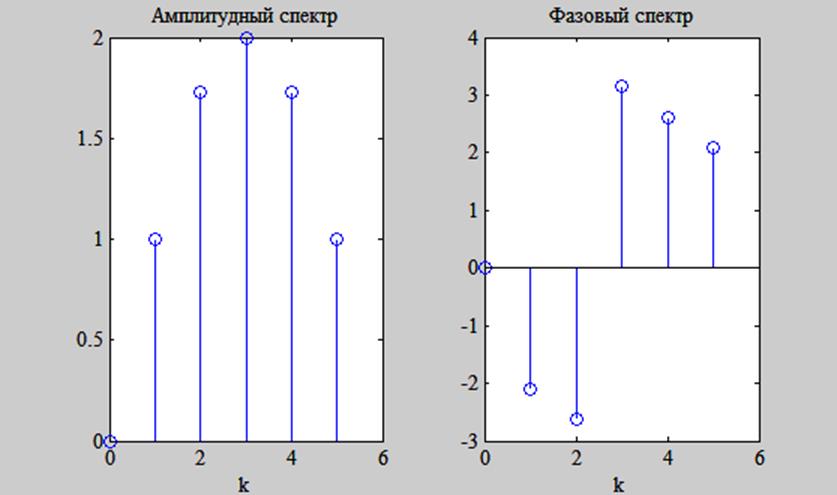
Рис. 11. Амплитудный и фазовый спектры сигнала при размере ДПФ 6 точек.

9.  Построение амплитудного спектра дискретного сигнала по заданному спектру аналогового для модели идеальной дискретизации.

Дан амплитудный спектр аналогового сигнала (рис.12).

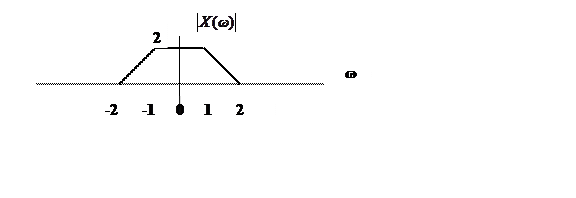
Рис. 12. Амплитудный спектр аналогового сигнала.

Дискретный сигнал получается из аналогового путём идеальной дискретизации ,  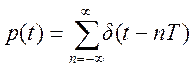 с периодом отсчётов  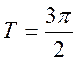сек.

При идеальной дискретизации сигнала спектральная плотность  дискретного сигнала связана со спектральной плотностью  аналогового сигнала  

выражением 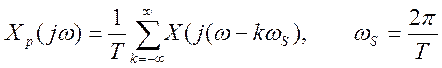(14).

                                                                              (14)

Здесь 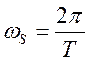   -  угловая частота дискретизации.

Из  выражения  (14) видно, что спектр дискретного сигнала, полученного дискретизацией аналогового, является периодическим и состоит из сдвинутых на ω_S  копий спектров  исходного сигнала.

При дискретизации с периодом отсчётов 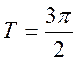 частота отсчётов .

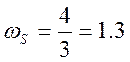Дискретизация с такой частотой не удовлетворяет условию теоремы отсчётов , поэтому спектры дискретного сигнала будут перекрываться.

Построим график амплитудного спектра заданного дискретного сигнала.

Результат представлен на рис. 13.

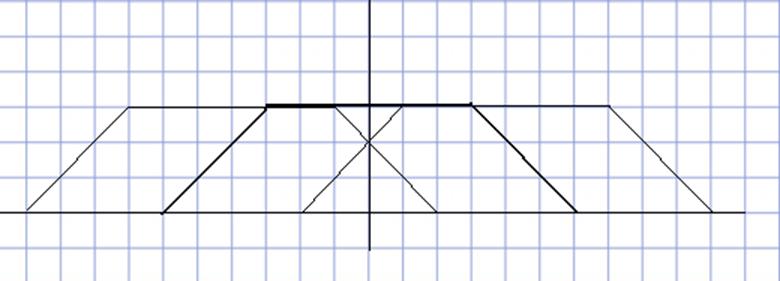
Рис. 13. График амплитудного спектра дискретного сигнала.

10.  Определение передаточной функции и частотных характеристик аналогового фильтра.

Дана схема аналогового фильтра (рис. 14).

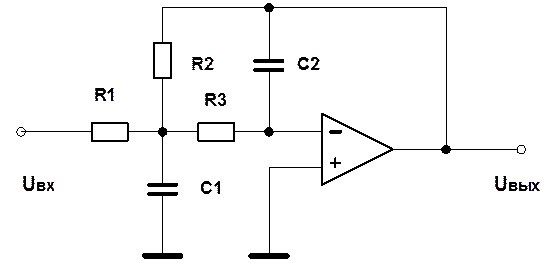
Рис. 14. Схема аналогового фильтра.

Определим передаточную функцию данного фильтра.

 Запишем выражения для проводимостей Y_i

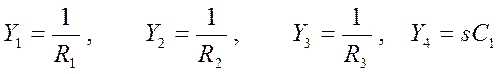,                                                     (15)

Выразим токи для узла A через напряжения и проводимости Y_i

.                                                                (16)

Отсюда выражение для потенциала узла А

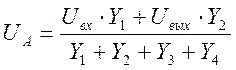                                                                                                                    (17)

Выражение для тока узла B

 .                                                                                                                       (18)

Отсюда

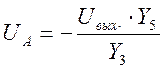.                                                                                                                            (19)

Подставляя (19) в  (17), приводя подобные члены и составляя отношение выходного напряжения  к входному, получаем

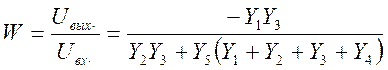                                                                                       (20)

Подставив выражения (15) в (20) и упростив результат, получим передаточную функцию аналогового фильтра

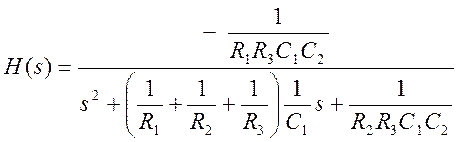                                                                (21)

Сделав замену  в передаточной функции (21), получим  -  частотную характеристику системы.

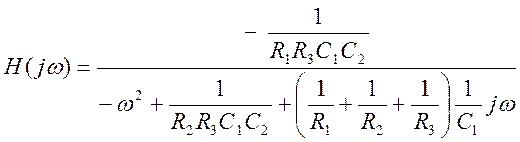                                                       (23)

Построим графики АЧХ и ФЧХ заданного аналогового фильтра при значениях сопротивлений и емкостей R1=5 кОм,   R2=1 кОм,  R3=2 кОм,     C1=1 мкФ,   C2=1 мкФ.

Результат представлен на рис. 15.

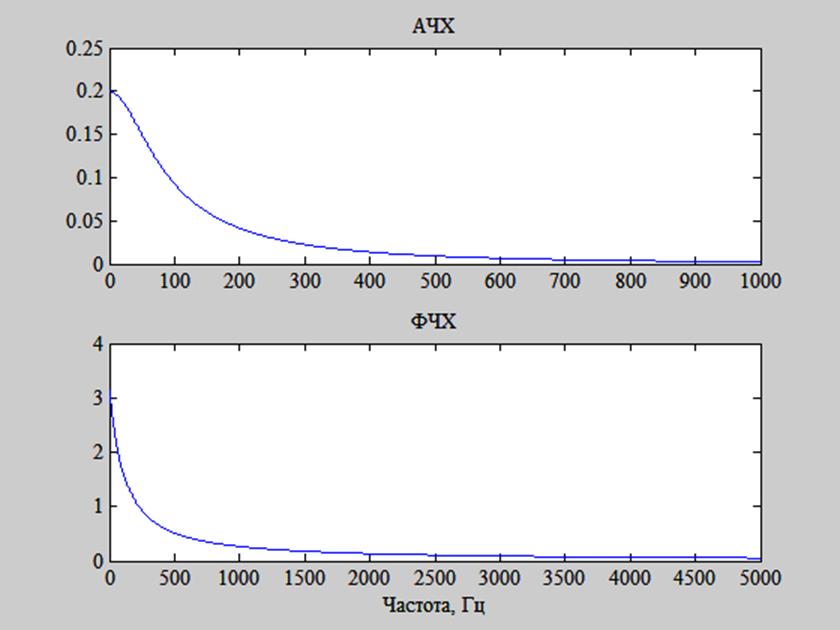
Рис. 15. АЧХ и ФЧХ аналогового фильтра.

По форме АЧХ видим, что схема представляет собой фильтр нижних частот, т.е. пропускает низкие частоты лучше, чем высокие.

Частота среза – это частота, при которой АЧХ снижается  до уровня

(в децибелах – на 3 дБ) от максимального значения.

Максимальное значение АЧХ .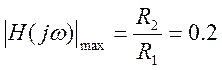

АЧХ снижается в  раз от на частоте .