Рис. 11.11
На рис. 11.12 приведена АЧХ цифрового фильтра при частоте дискретизации 10000 Гц.
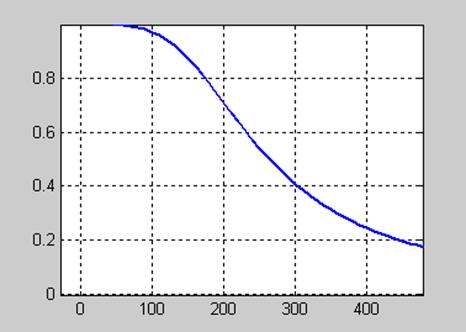
Рис. 11.12
10. Используя метод билинейного преобразования, рассчитать передаточную функцию цифрового ФНЧ с частотой среза по уровню 3 дБ ωС =100 Гц и частотой дискретизации Т = 1 кГц, аппроксимирующего передаточную функцию аналогового ФНЧ второго порядка Баттерворта.
Решение.
Передаточная функция нормированного (с единичной
угловой частотой среза) ФНЧ Баттерворта второго порядка имеет вид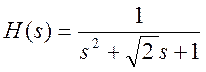 
.
Определим критическую частоту (частоту среза) аналогового прототипа с помощью тангенциального преобразования
.
С помощью формулы частотного преобразования трансформируем нормированный ФНЧ в ФНЧ с частотой среза ΩС
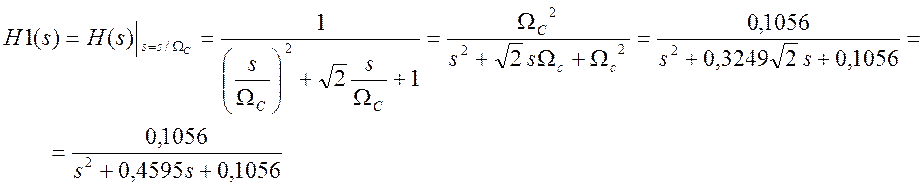
H1(s) является передаточной функцией аналогового прототипа для цифрового фильтра.
На рис. 11.13 показана АЧХ фильтра с передаточной функцией H1(s)
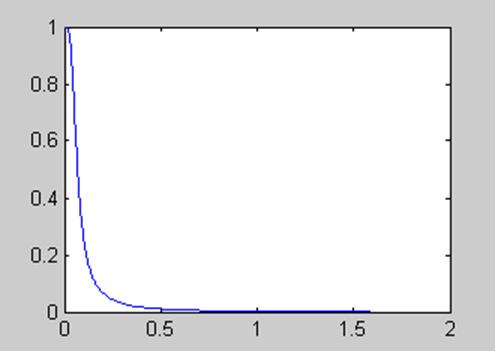
Рис. 11.13
Переход к цифровому фильтру
выполним с помощью билинейного преобразования путем подстановки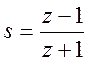 
в передаточную функцию H1(s)
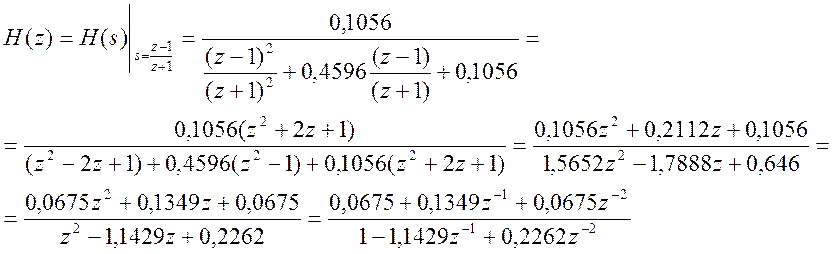
На рис. 11.14 представлена АЧХ цифрового ФНЧ с передаточной функцией H(z) при частоте дискретизации 1000 Гц
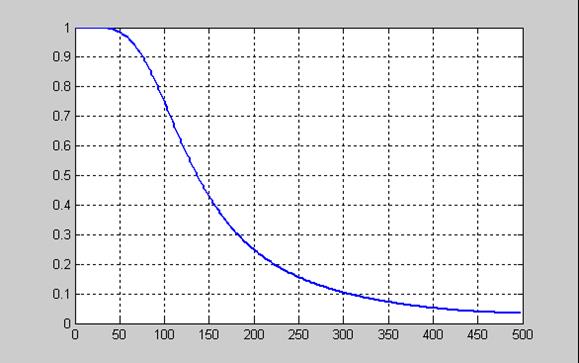
Рис. 11.14
Уравнение фильтра 
.
11. На основе метода билинейного преобразования спроектировать цифровой фильтр верхних частот Баттерворта с частотой среза ωС = 50 Гц и частотой дискретизации
500 Гц.
Решение.
Передаточная функция
нормированного ФНЧ 1-го порядка Баттерворта имеет вид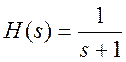 
.
Находим нормированную граничную частоту полосы пропускания аналогового фильтра – прототипа с помощью тангенциального преобразования
.
С помощью преобразования «ФНЧ -> ФВЧ» определим передаточную функцию аналогового прототипа
.
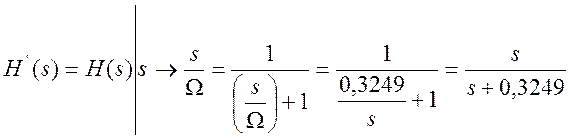Для получения передаточной функции цифрового ФВЧ применим билинейное преобразование
.
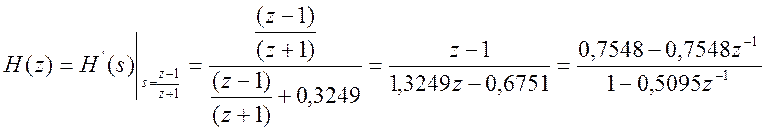Уравнение фильтра
.
На рис. 11.15 показана АЧХ полученного ФВЧ с передаточной функцией H(z)
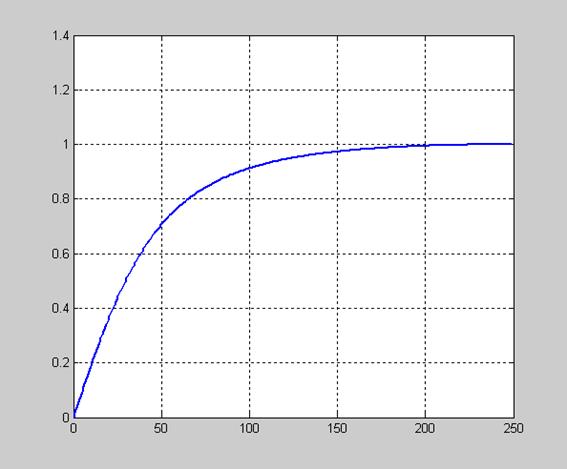
Рис. 11.15
12. Используя метод
сглаживающих окон, спроектируйте КИХ - фильтр нижних частот со следующей
спецификацией:
- допустимый уровень отклонений АЧХ в полосе пропускания 
;
- допустимый уровень отклонений
АЧХ в полосе задерживания 
;
- граничная частота полосы пропускания 500 Гц;
- граничная частота полосы задерживания 800 Гц.
Решение.
Проектирование фильтра на основе метода взвешивающих окон заключается в выборе типа окна, определении порядка и коэффициентов (значений импульсной характеристики) уравнения фильтра.
1.
Выберем частоту дискретизации (отсчетов) в соответствии с требованиями
теоремы отсчетов равной 2000 Гц, при этом частота Найквиста равна 1000 Гц.
Нормированные граничные частоты полосы пропускания и полосы задерживания
окажутся равными 
Гц/отсчет и 
Гц/отсчет соответственно. Частота
среза фильтра
Гц/отсчет, соответственно 
Ширина переходной полосы фильтра 
Гц/отсчет, нормированная угловая
переходная полоса 
.
2.
Определим допустимый уровень пульсаций как 
или
в децибелах 
. Такому уровню ошибки
аппроксимации идеальной АЧХ фильтра соответствует окно Блэкмана, для которого допустимый
уровень пульсаций A = 74 дБ. Поэтому для дальнейшей
реализации фильтра выбираем окно Блэкмана.
3. Определяем порядок фильтра с окном Блэкмана по выражению
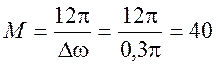
4.
Окно Блэкмана для фильтра
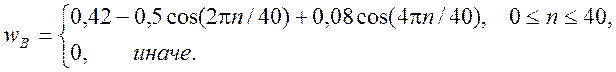
5.
Импульсная характеристика рассчитанного фильтра
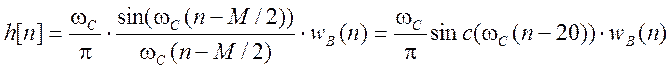
На рис. 11.16 представлена АЧХ спроектированного фильтра в линейном масштабе, а справа –график пульсаций в полосе пропускания.
|
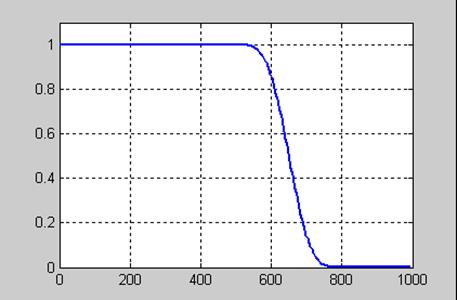
Рис. 11.16
Приведенные на графиках результаты свидетельствуют, что спроектированный фильтр удовлетворяет исходным требованиям.
Задачи для самостоятельного решения.
1.
Найдите частоту среза на уровне 3 дБ фильтра с передаточной функцией
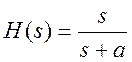
Ответ: 
.
2.
Найдите импульсную характеристику, передаточную функцию, АЧХ и ФЧХ разностного
фильтра с уравнением 
. Изобразите и
объясните график АЧХ.
Ответ: 
.
3.
Найдите порядок ФНЧ Баттерворта, который должен иметь ослабление Amax=1 дБ на частоте 10 Гц и Amin=45
дБ на частоте 20 Гц.
Ответ. N = 9.
4.
Определите тип и АЧХ фильтра с уравнением 
.
Ответ. ФВЧ,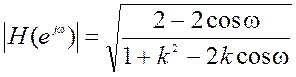 
.
5. Фильтр нижних частот Чебышева 1-го рода имеет следующие параметры:
ΩP = 2,1 , ΩS = 8 , Amax = 0,5 дБ , Amin = 60 дБ. Определите необходимый порядок фильтра.
Ответ: N = 3.
6. Найдите минимально необходимый порядок для инверсного режекторного чебышевского фильтра с параметрами :
.
Ответ: для РФ N = 4 (для ФНЧ, как прототипа, N = 2).
7.
Определите тип фильтра и найдите частоту среза на уровне 3 дБ. Уравнение
фильтра
а) 
,
б) 
.
8. Рассчитайте аналоговый ФНЧ Чебышева 1-го рода со спецификацией:
.
9. Рассчитайте цифровой ФНЧ Баттерворта с частотой среза на уровне 3 дБ = 800 Гц, минимальным затуханием на граничной частоте полосы задерживания 1000 Гц, равным 30 дБ, частотой отсчетов 4000 Гц.
10.
Выходной сигнал КИХ - фильтра формируется с помощью усреднения текущего
и предыдущего отсчетов. Определите для такого фильтра
а) импульсную характеристику,
б) АЧХ,
в) выходной сигнал, если входной дискретный синусоидальный
сигнал имеет частоту
10 Гц и частоту отсчетов 100 Гц.
11. Используя сглаживающее окно Хэмминга длиной М = 31, получите импульсную характеристику нерекурсивного фильтра нижних частот с частотой среза 200 Гц и частотой отсчетов 1000 Гц. Постройте АЧХ сглаженного фильтра и объясните её поведение.
12. Рассчитайте КИХ - фильтр нижних частот с исходными требованиями
· Нормированная граничная частота полосы пропускания ΩP = 0,45π
· Нормированная граничная частота полосы задерживания ΩS = 0,6π
·
Допустимые пульсации в полосе пропускания 
·
Допустимые пульсации в полосе задерживания 
.
Составил: доц.
Щетинин Ю.И.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
