Задачи 3
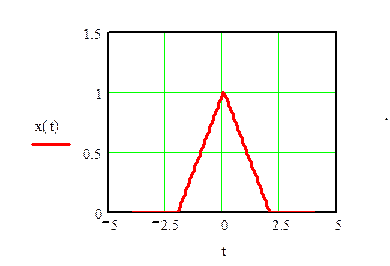 Определить
преобразование Фурье треугольного импульса и построить график его
амплитудного спектра
Определить
преобразование Фурье треугольного импульса и построить график его
амплитудного спектра 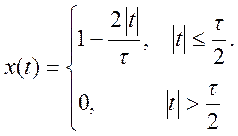
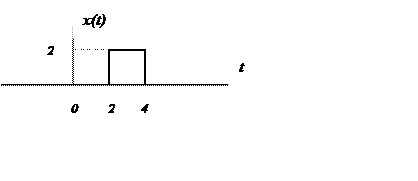
График для τ =4.
Решение.
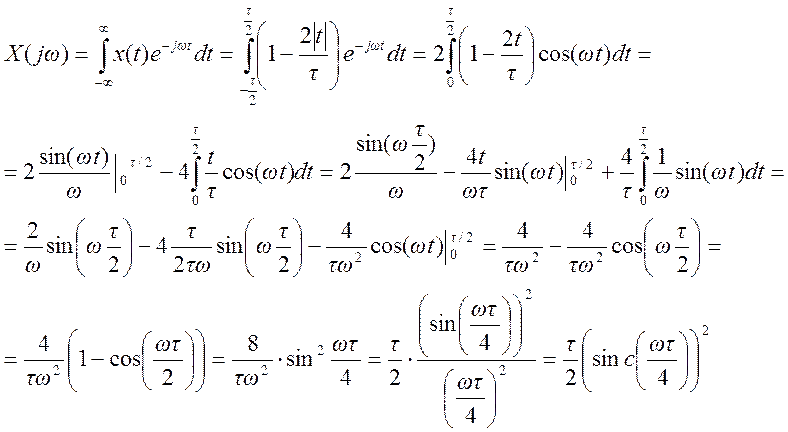
График амплитудного спектра
сигнала при ![]()
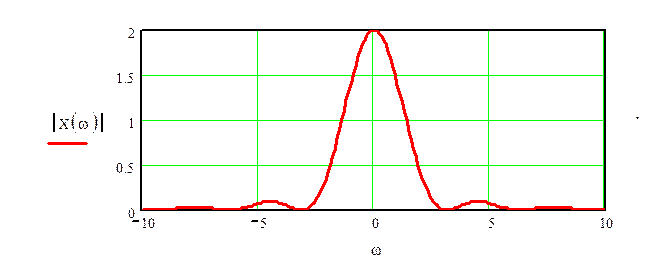
Решение.
Определим спектр Фурье прямоугольного импульса длительностью τ, симметричного относительного начала координат.
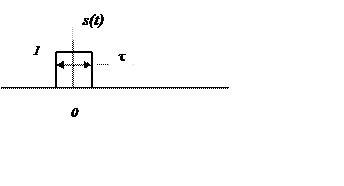

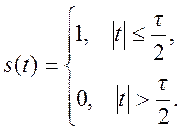
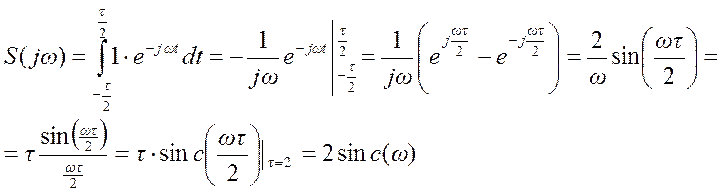
Связь между сигналами x(t) и s(t) x(t) = 2s(t-3)
По свойству линейности и временного сдвига преобразования Фурье
![]() .
.
Решение.
Преобразование Фурье
правостороннего экспоненциального сигнала ![]()
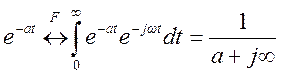 .
Поэтому
.
Поэтому 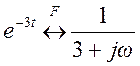 .
.
Согласно свойству частотного сдвига
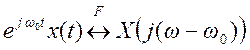 ,
следовательно, для
,
следовательно, для 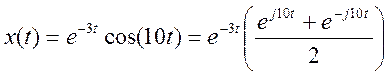
преобразование Фурье
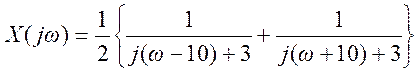 .
.
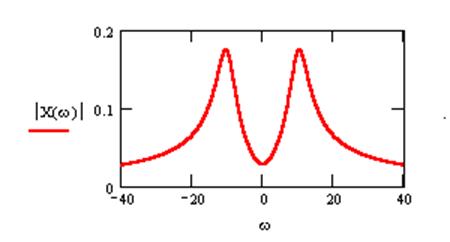
График амплитудного спектра сигнала
Комментарий: пики на частотах ω = ±10
соответствуют переносу (сдвигу) спектра
сигнала ![]() в связи с его модуляцией
в связи с его модуляцией
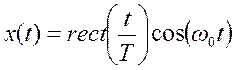 ,
где
,
где 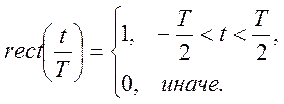
Решение
Преобразования Фурье
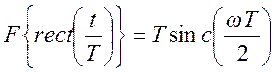 ,
,
![]() .
.
По свойству умножения преобразования Фурье произведению сигналов во временной области соответствует свертка их преобразований Фурье в частотной области
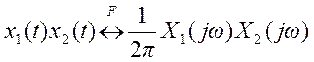 .
.
Поэтому
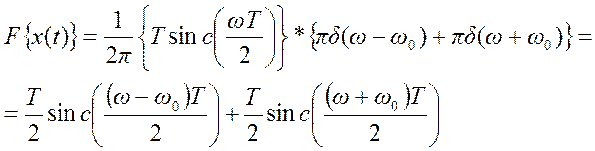
5. Определить спектр Фурье
сигнала 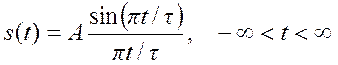 .
.
Решение.
Используем свойство дуальности преобразования Фурье.
Если ![]() .
.
Прямоугольному импульсу x(t) с амплитудой А и длительностью ![]() , симметричному относительно начала
координат, соответствует преобразование Фурье
, симметричному относительно начала
координат, соответствует преобразование Фурье
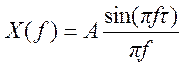 .
.
Следовательно, по свойству дуальности сигналу
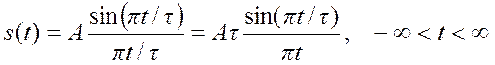 отвечает преобразование
Фурье вида
отвечает преобразование
Фурье вида
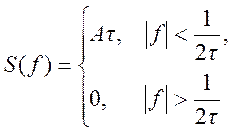
Графики для А=1 и τ=2
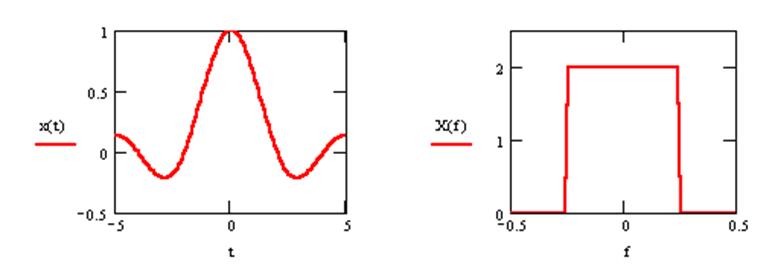
6. Преобразование Фурье сигнала
имеет вид 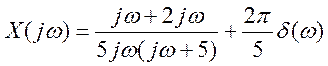 .
.
Найти вид сигнала во временной области.
Решение.
Представим ![]() как
как 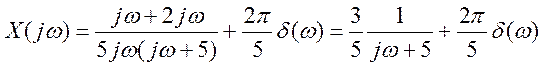 .
.
Используя таблицу преобразований
Фурье, определяем оригиналы во временной области, соответствующие слагаемым ![]()
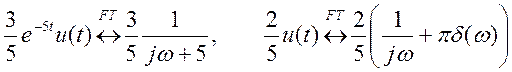 ,
где u(t) – единичная
ступенчатая функция.
,
где u(t) – единичная
ступенчатая функция.
Поэтому 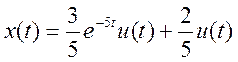 .
.
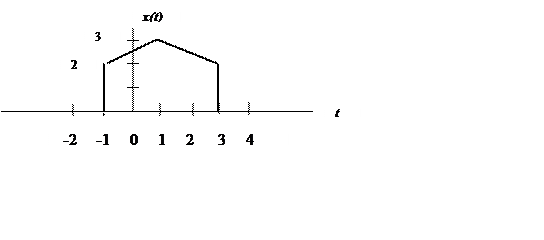
Найти
а) X(0),
б) 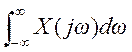 , в)
, в) 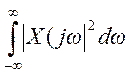
Решение.
а) 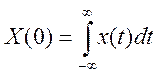 ,
поэтому
,
поэтому ![]() .
.
б) 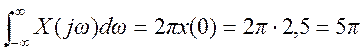 .
.
в) По теореме Парсеваля 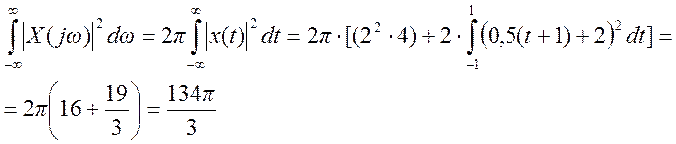
8. Найти преобразование
Фурье сигнала
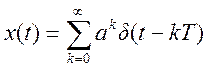 , где
, где ![]() -
дельта – функция,
-
дельта – функция, ![]() .
.
Решение.
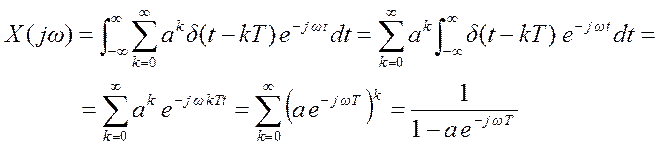
При преобразовании этого выражения использовалась сумма геометрической прогрессии.
9. Вычислить свертку сигналов x(t) и h(t) с использованием свойства свертки преобразования Фурье
![]() - единичная ступенчатая
функция.
- единичная ступенчатая
функция.
Решение.
Свертке 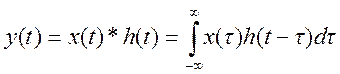 во
временной области соответствует произведение преобразований Фурье в частотной
области, т.е.
во
временной области соответствует произведение преобразований Фурье в частотной
области, т.е. ![]() .
.
Преобразование Фурье
односторонней экспоненты 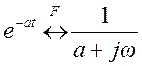 , поэтому
, поэтому
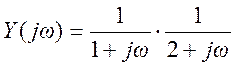 .
Разложим Y(jω) на простые
дроби
.
Разложим Y(jω) на простые
дроби
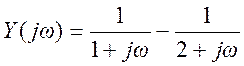 .
Применим к Y(jω) обратное
преобразование Фурье, получим
.
Применим к Y(jω) обратное
преобразование Фурье, получим ![]() .
.
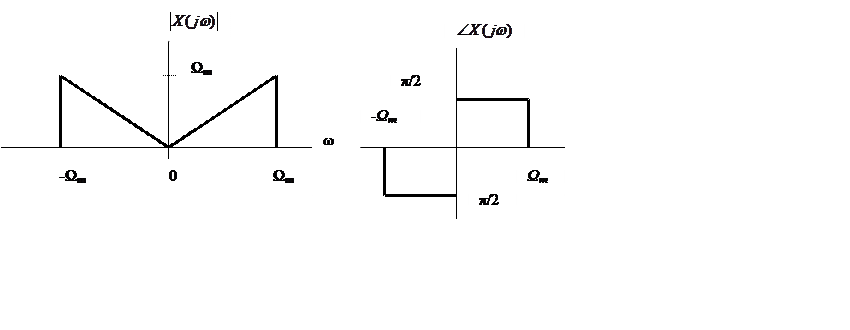 10.
Заданы графики амплитудного и фазового спектров сигнала. Определить вид
сигнала во временной области.
10.
Заданы графики амплитудного и фазового спектров сигнала. Определить вид
сигнала во временной области.
Решение.
Предположим сигнал y(t) с равномерным спектром следующего вида
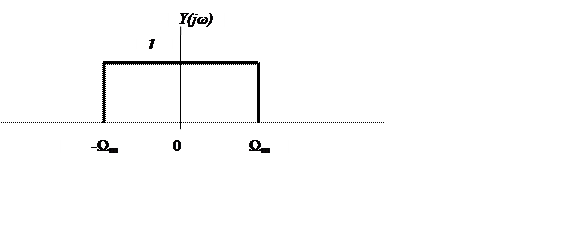 |
Это сигнал с единичной спектральной плотностью амплитуды в
полосе частот ![]() .
.
По свойству
дифференцирования преобразования Фурье ![]() .
.
Следовательно,
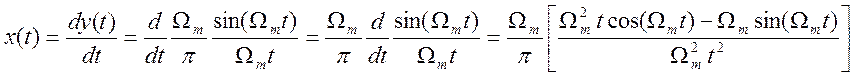 .
.
Задачи для самостоятельного решения
![]() .
.
Ответ: 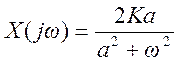
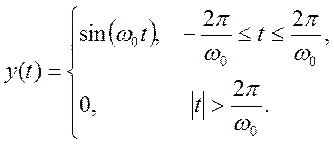
Ответ. 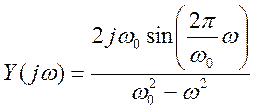
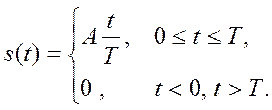
Ответ: 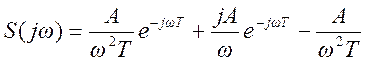
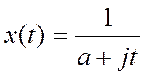
Ответ: ![]()

Ответ: ![]()
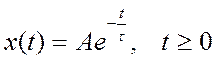
Ответ: для А = 2, ![]()
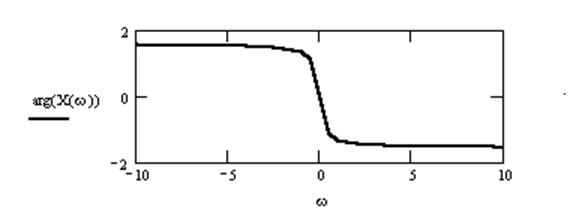
7. Дано дифференциальное уравнение, связывающее вход x(t) и выход y(t) системы
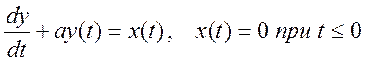 .
.
Найдите преобразование Фурье этого уравнения. Определите отношение
преобразований Фурье левой и правой части, т.е. 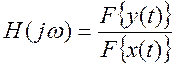 .
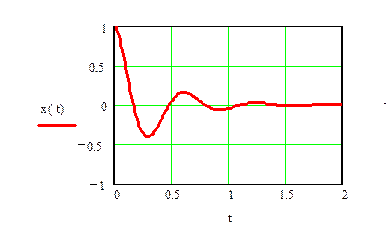
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
.
Постройте приближенные графики модуля и фазы этого отношения от частоты. Дайте
интерпретацию смысла функций на графиках.
Ответ. 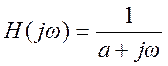 .
.
8. Найдите преобразование Фурье и постройте приближенный вид графика амплитудного спектра следующего сигнала
![]() ,
где u(t) - единичная
ступенчатая функция.
,
где u(t) - единичная
ступенчатая функция.
Ответ: 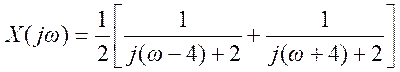 .
.
9. Найдите вид сигнала во временной области, если преобразование Фурье сигнала имеет вид
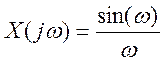 .
.
Ответ. 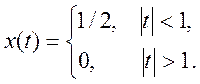
10. Постройте
амплитудный спектр сигнала
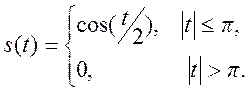
Ответ. 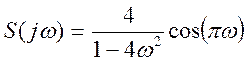
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.