НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Расчетно-графическая работа по курсу
«Теория и обработка сигналов»
5 - й семестр
Вариант –9,10.
Cтудент: Скориков С. Преподаватель:
Факультет: АВТ Еленычев С.В.
Группа АО-31
Новосибирск
2005
Раздел 1.
1.9. Является ли
линейной и инвариантной во времени система с уравнением ![]() ?
?
Ответ.
Система – линейная, неинвариантная во времени.
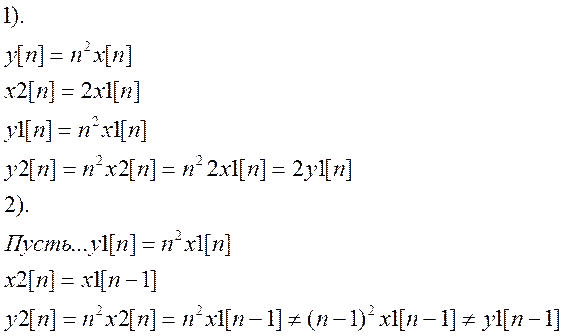
Из первого пункта можно сделать вывод о том, что система линейная, а из второго – о то, что она неинвариантная во времени (нестацинарная).
1.10 . Определите,
является ли линейной, стационарной (инвариантной во времени) и устойчивой
система- интегратор с уравнением 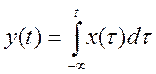 ?
?
Ответ. Система - линейная, инвариантная во времени, но неустойчивая.
Пусть x2(t)=2x1(t), тогда y2(t)=2y1(t), так как 2 – это постоянная и выносится за знак интеграла. Значит система является линейной.
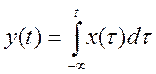
![]()
Найдем значение интеграла при условии, что будет отставание переменной на τ0:
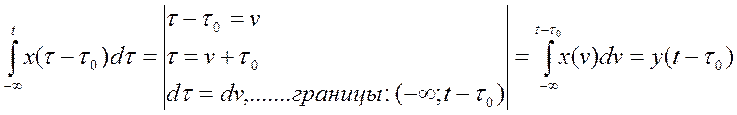
Что доказывает то, что система инвариантная во времени.
Для устойчивой системы ограниченному входному сигналу должен соответствовать ограниченный выходной сигнал, что не обеспечивается, благодаря взятию интеграла от
-![]() и
до неизвестного t.
и
до неизвестного t.
Раздел 2.
2.9.
Определите амплитудный и фазовый спектры периодического сигнала и постройте их
графики

Ответ. 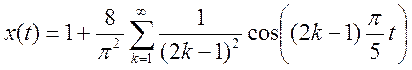
Т=10
w0=π/5
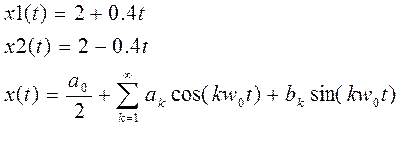
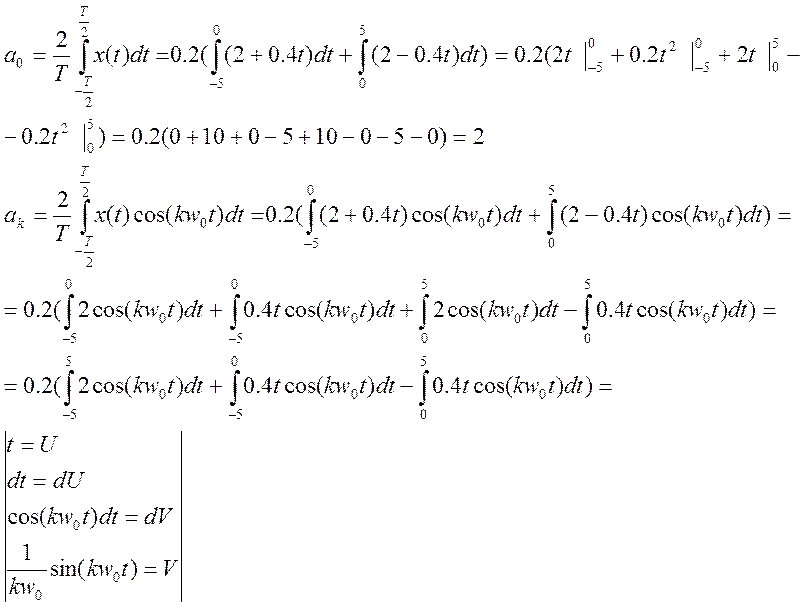
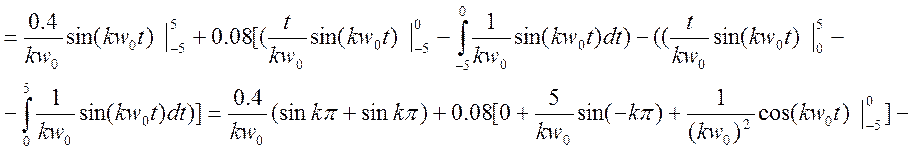
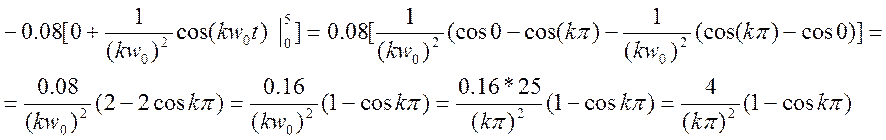
При четных k коэффициент обращается в 0, а при нечетных – в 2. Поэтому его можно упростить:
![]()
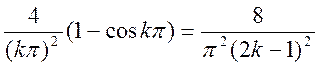
Так как функция четная, то второй коэффициент равен 0.
Ряд Фурье :
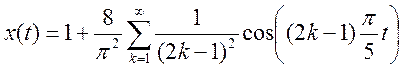
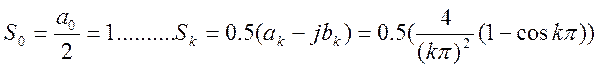
Амплитудный спектр:
Фазовый спектр является величиной
постоянной и равен 0, так как ![]() - коэффициент
комплексного ряда Фурье принимает действительные значения для любого k.
- коэффициент
комплексного ряда Фурье принимает действительные значения для любого k.
2.10. Определите амплитудный
и фазовый спектры периодического сигнала и постройте их графики
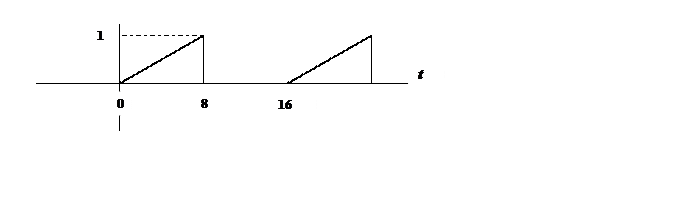
Ответ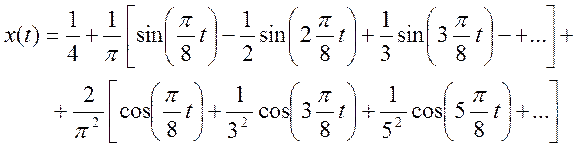
Т=16, w0=
![]()
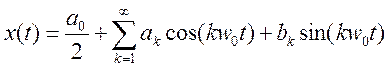
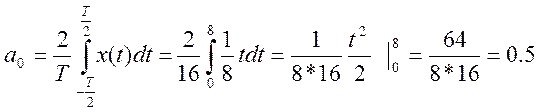
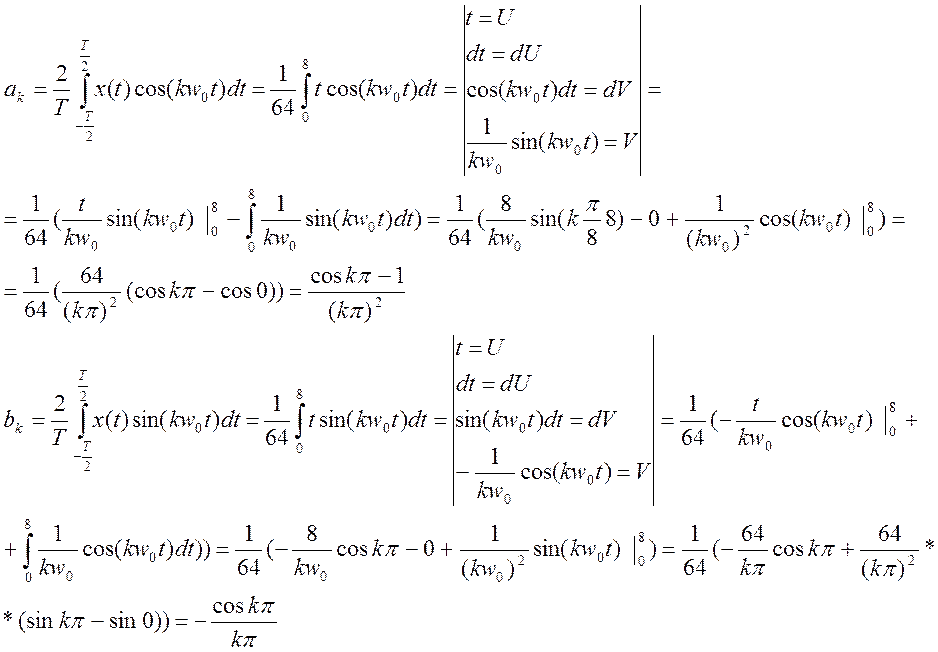
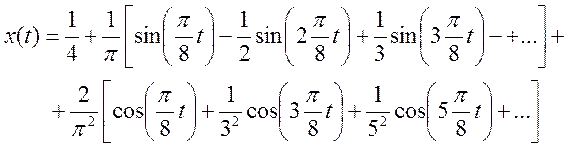
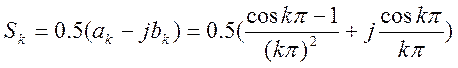
k=-10:1:10;
x=cos(k*pi)-1;
y=x./(k*pi).^2;
f=cos(k*pi)./(k*pi);
z=(y+j*f)./2;
subplot(211);
plot(k,abs(z));
subplot(212);
plot(k,angle(z));
Амплитудный и фазовый спектры:
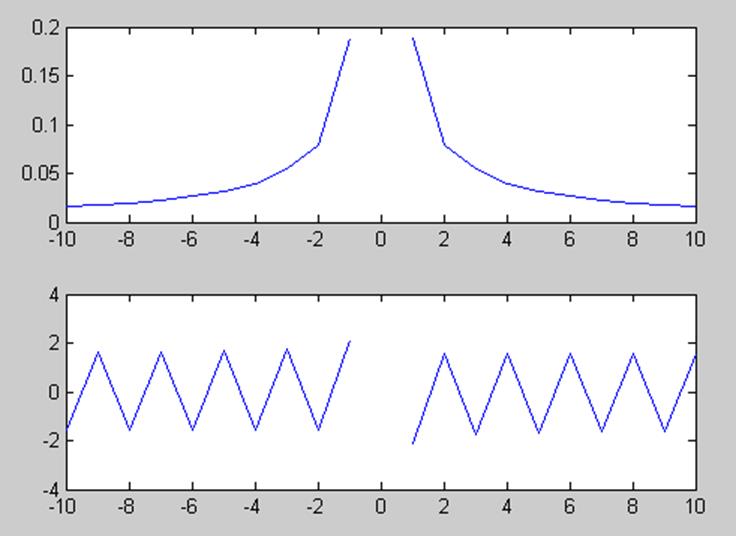
В нуле амплитуда равна:
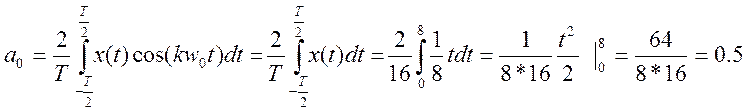
bk=0
![]()
Фаза в 0 равна 0, так как второй коэффициент равен 0.
Раздел 3.
3.9. Найдите вид сигнала во временной области, если преобразование Фурье сигнала имеет вид
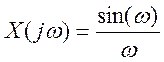 .
.
Ответ. 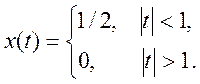
Так как интеграл от произведения заданной функции и экспоненты, зависящей от w взять практически очень тяжело, то мы можем воспользоваться результатами вычислений прямого преобразования Фурье, известно, что
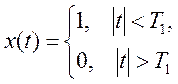 соответствует ПФ=
соответствует ПФ= 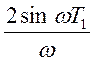 , поэтому x(t) для заданного ПФ
, поэтому x(t) для заданного ПФ
Будет иметь вид: 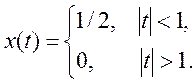 , так как Т1=1, и в ПФ присутствует
коэффициент, равный 2.
, так как Т1=1, и в ПФ присутствует
коэффициент, равный 2.
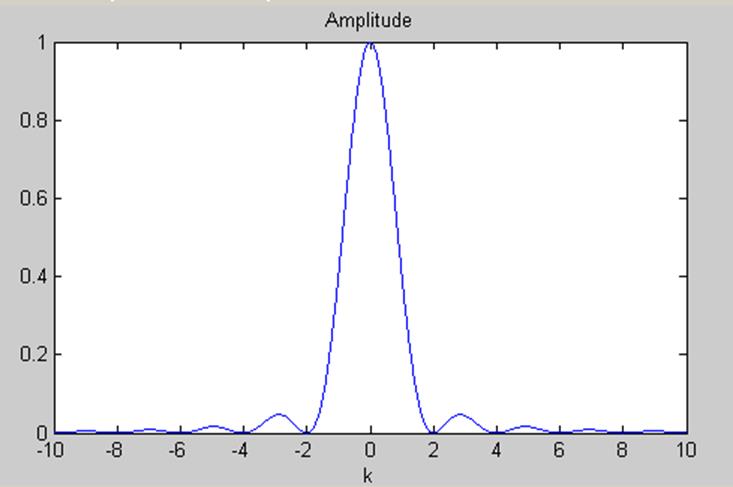
3.10. Постройте амплитудный
спектр сигнала
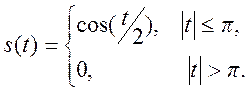
Ответ. 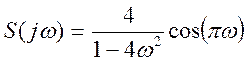
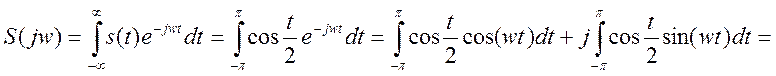
Так как второй интеграл от нечетной функции на симметричном интервале, то он равен 0.
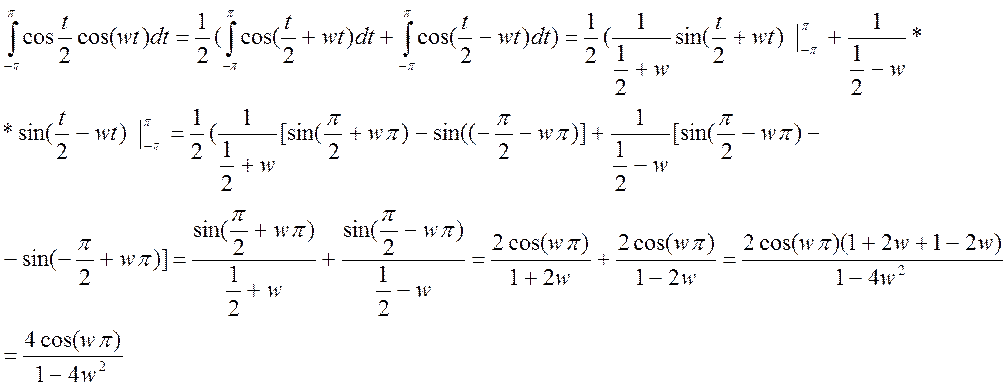 w=-10:0.01:10;
w=-10:0.01:10;
x=cos(w*pi)./(1-4*w.^2);
plot(w,abs(4*x));
title('Amplitude')
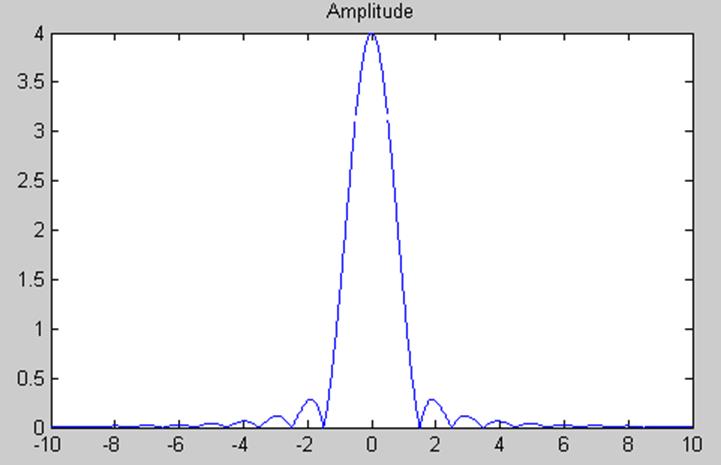
В точках ![]() амплитуда равна:
амплитуда равна:
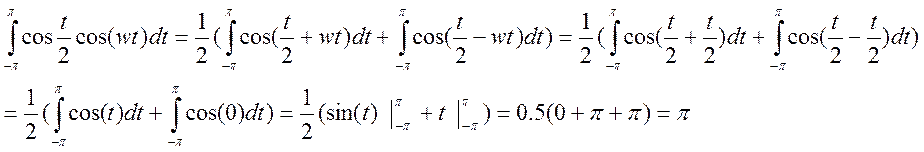
Раздел 4.
4.9.
Вычислите ДВПФ и ДПФ сигнала ![]() .
.
Ответ. ![]() ,
, ![]()
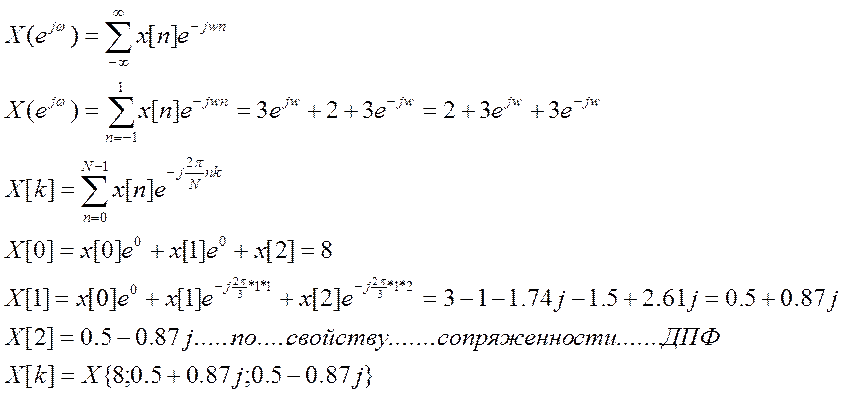
4.10. Вычислите ДПФ для
сигнала ![]() .
.
Ответ. ![]() .
.
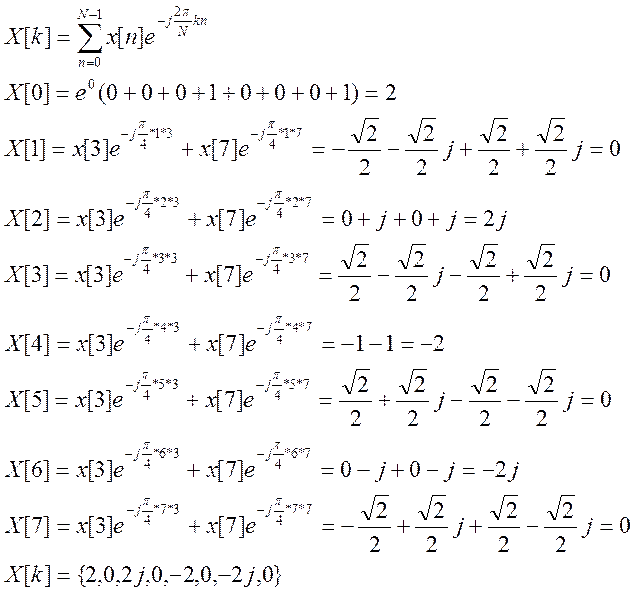
Раздел5.
5.9. Вычислите свертку двух
непрерывных сигналов и изобразите её график
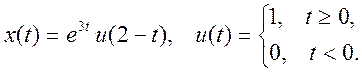
![]() .
.
Ответ. 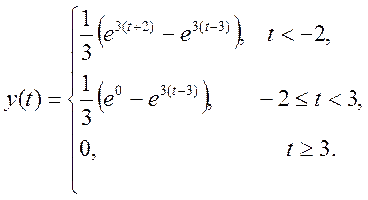
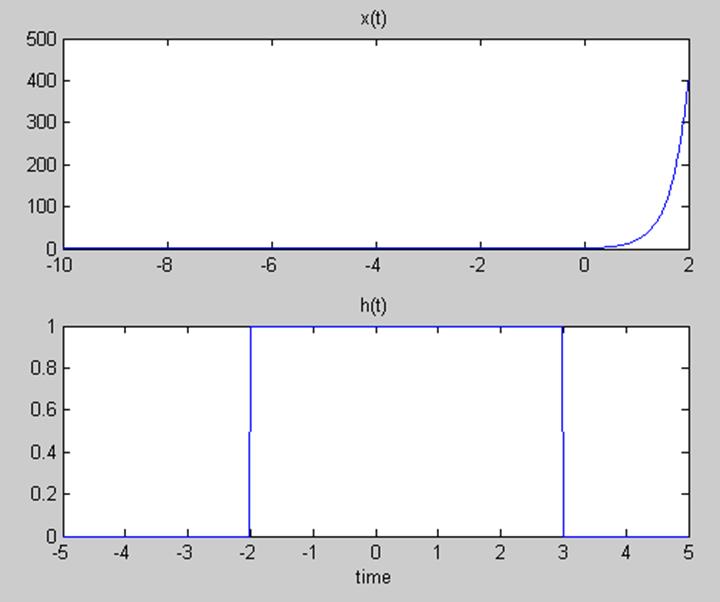
Сформируем эти сигналы:
t=-10:0.01:2;
x=exp(3*t);
subplot(211);
plot(t,x);
title('x(t)');
T=-5:0.01:5;
h=rectpuls(T-0.5,5);
subplot(212);
plot(T,h);
title('h(t)');
xlabel('time');
В данном случае лучше взять x(t-τ). Получим выражение для свертки:
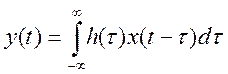
При «зеркальном отображении» сигнала x(t), относительно оси ординат, а так же его сдвиге на t=3, пересечение с сигналом h(t) будет равно нулю. Поэтому для всех t>3, y(t)=0. Для t, лежащим в интервале от -2 до 3, свертка будет иметь вид:
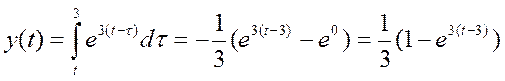
Если же t<= -2 то свертка будет иметь вид:
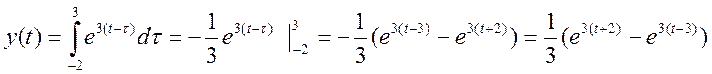
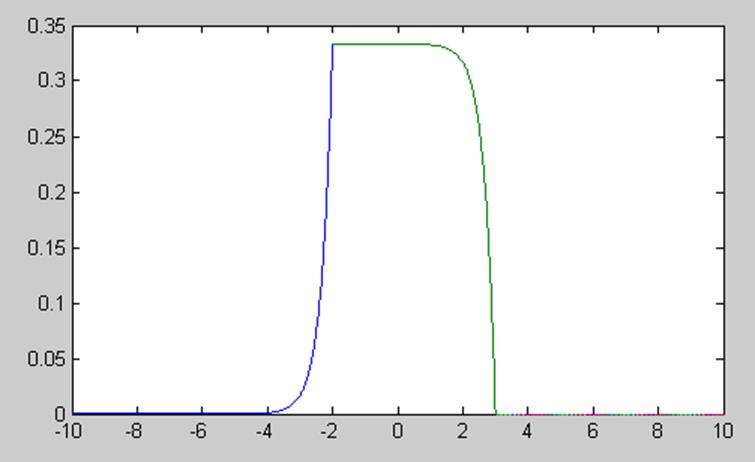
График свертки:
t1=-10:0.01:-2;
x=(1./3).*(exp(3*t1+6)-exp(3*t1-9));
t2=-2:0.01:3;
y=(1./3).*(1-exp(3*t2-9));
t3=3:0.01:10;
z=0;
plot(t1,x,t2,y,t3,z);
5.10. Вычислите
дискретную свертку сигнала 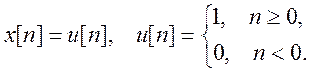
и сигнала 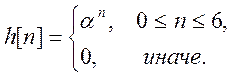
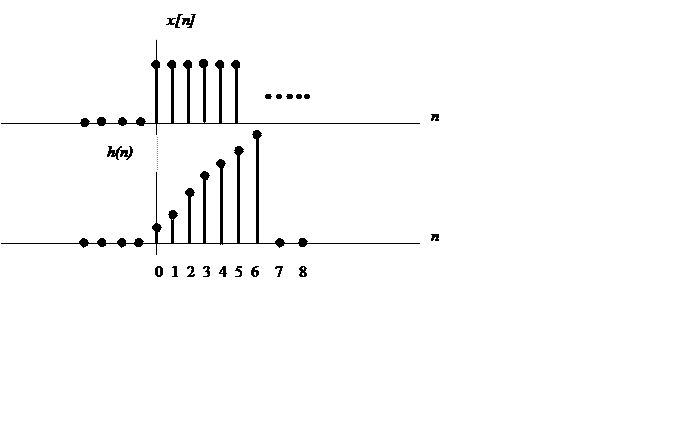
Постройте график свертки.
Ответ. 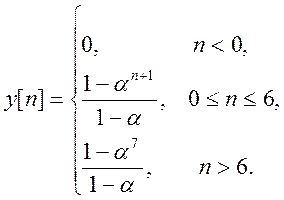
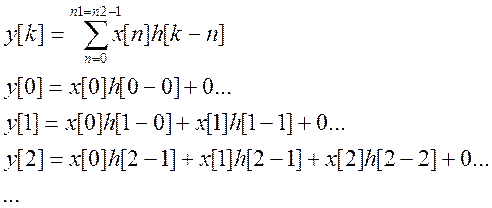
Так как первый сигнал – бесконечной и равен 1 в каждой точке, то свертка будет «зависеть» от второго сигнала, который ограничен числом отсчетов=7.
Как видно из вышеуказанных формул свертка равна:
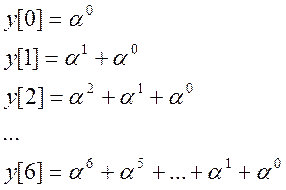
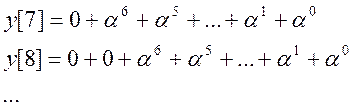
То есть свертка сигнала равна:
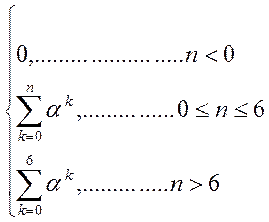
Если ![]() <0,
то сумма является суммой бесконечно убывающей геометрической прогрессии.
<0,
то сумма является суммой бесконечно убывающей геометрической прогрессии.
Эту сумму можно представить в виде:
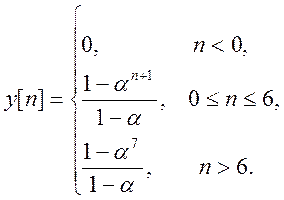
Построим график для ![]() =0,5:
=0,5:
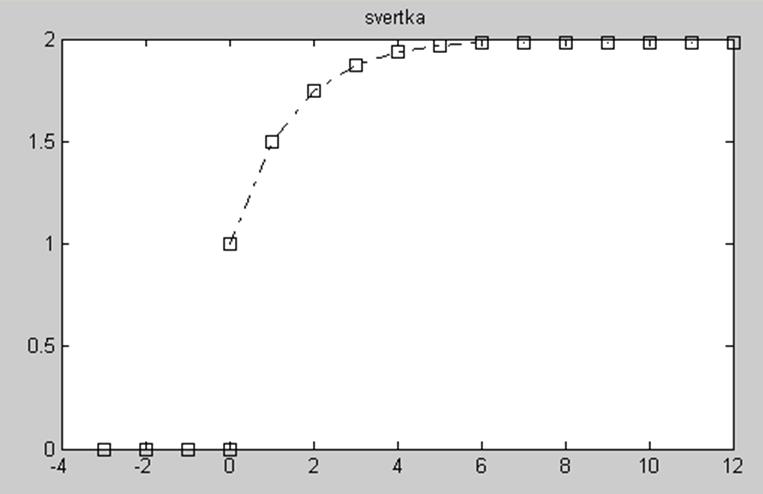
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.