Определение линейной и инвариантной во времени дискретной системы. Определение выходного сигнала системы. Поиск импульсной характеристики, АЧХ и ФЧХ системы, страница 2

.

10.  Задана передаточная функция системы
.
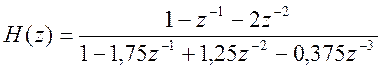Найдите её полюсы и нули и постройте диаграмму нулей и полюсов.
Решение.
Умножая числитель и знаменатель передаточной функции на z², получим
.  
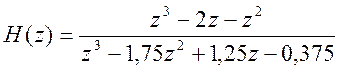Методом подбора, найдем первый корень знаменателя, равный  p₁ = 0,75. Далее разложим знаменатель с выделением (z-0,75) и определим корни квадратного уравнения
z² – z + 0,5 = 0. Таким образом,  значения полюсов

Ещё более просто находим корни числителя, т.е. нули

Диаграмма нулей и полюсов

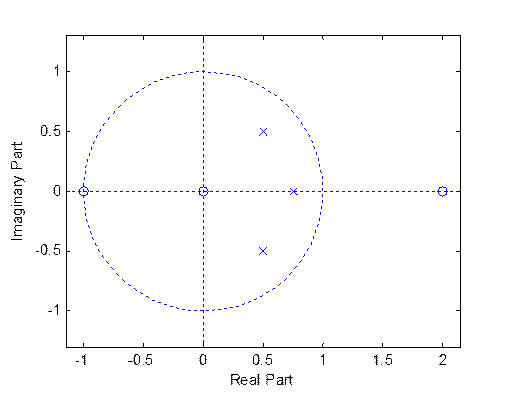
Через нули и полюса можно записать передаточную функцию с точностью до множителя – константы

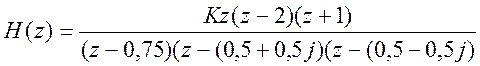
11.     Пусть передаточная функция системы задана в виде

.

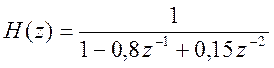 Найдите переходную характеристику (реакцию на единичное входное воздействие) системы.

Решение.

В  Z – области выражение связи вход – выход имеет вид  . Для входного сигнала в виде единичной функции    Z - преобразование  .  

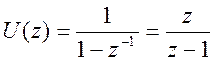Определяя  корни знаменателя, запишем  H(z)  в полюсно - нулевой форме 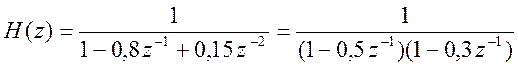.  При этом  Z – преобразование переходной характеристики

.

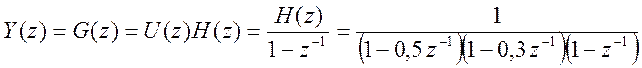Разложение  G(z)  на простейшие дроби дает выражение

.

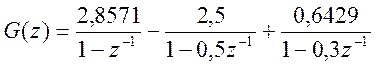Выполняя обратное  Z – преобразование, получаем переходную характеристику g[n]

12.  Уравнение линейной дискретной системы имеет вид .         Найдите выражение АЧХ системы, определите тип фильтра по характеру АЧХ.
Решение.

Передаточная функция  системы 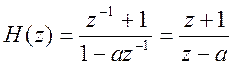     .   Система имеет полюс при   и нуль при .   Подставляя  , получаем частотную характеристику системы 

.

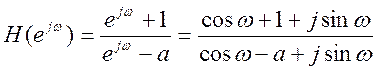Отсюда АЧХ системы  .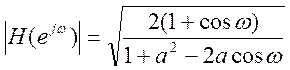

При  , т.е. на постоянном токе, АЧХ имеет максимум,   при  АЧХ минимальна, поскольку  знаменатель выражения будет максимальным.  Поэтому тип фильтра  - фильтр нижних частот. Это подтверждается графиком  АЧХ  для     а = 0.3  (рис. 9.6).

Обратите внимание на периодичность ЧХ.

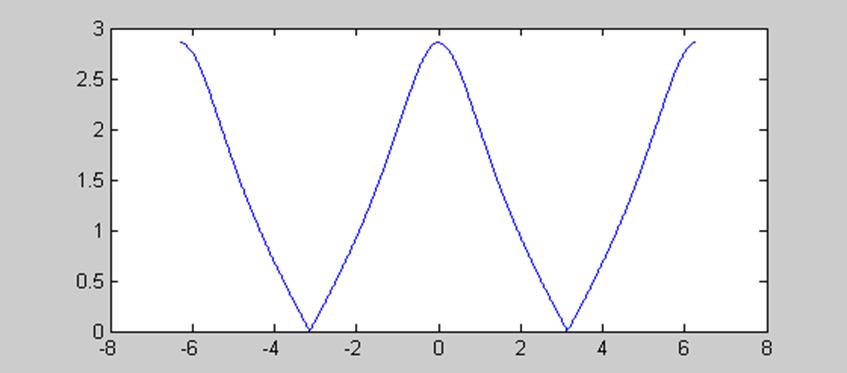
Рис. 9.6.

13.  Линейная дискретная система имеет отклик 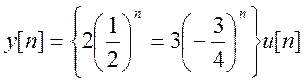  на входной сигнал вида .  Найдите
а) передаточную функцию системы,

б) полюса и нули,

в) импульсную характеристику,

г) уравнение системы.

Решение.

Для нахождения H(z)  определим Z – преобразования заданных x[n] и y[n]:

.

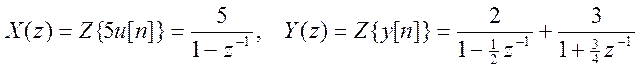Отсюда   .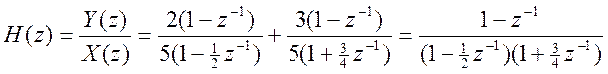

Нули и полюса  системы:   .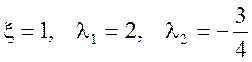

Импульсная характеристика может быть определена как обратное Z – преобразование  передаточной функции H(z).   Для этого разложим  H(z) на простые дроби и найдем константы (вычеты) разложения

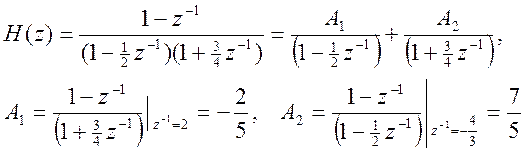
Следовательно,    .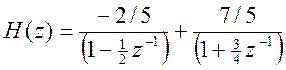

Выполняя обратное  Z – преобразование  от H(z) как суммы простых дробей, находим импульсную характеристику системы в виде

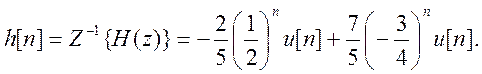
Для получения уравнения системы перепишем H(z) в виде

.

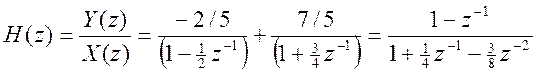Отсюда  .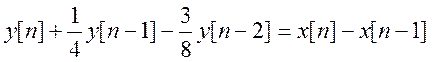

Задачи для самостоятельного решения.

1.  Определите, является ли линейной и каузальной система с уравнением
?
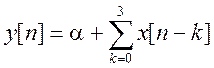Ответ. Линейная, каузальная система.

2.  Является ли линейной и инвариантной во времени система с уравнением
, где x[n] – входной сигнал?

Рис. 9.7.

Ответ.  Линейная, неинвариантная во времени система.

3.  Для ДВ ЛCC системы заданы входной сигнал x[n] и импульсная характеристики h[n]. Найдите выходной сигнал с помощью дискретной свертки.

Ответ. .

4.    Определите  импульсную характеристику, передаточную функцию, АЧХ и ФЧХ суммирующего фильтра     .
Ответ.   .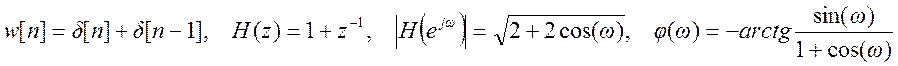

5.  Система состоит из двух последовательно соединенных звеньев (см.  рис.)

Рис. 9.8.

Система 1 имеет разностное уравнение  .  Система 2 имеет импульсную характеристику  .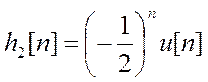

Найдите частотную  характеристику  всей системы.

Указание.  Определите  частотную характеристику системы 1 по её уравнению и системы 2, используя ДВПВ импульсной характеристики, затем перемножьте частотные характеристики.

Ответ.      .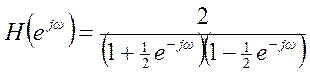

6.  Найдите входной сигнал  x₁[n] для системы из предыдущей задачи, если выходной сигнал   .

Указание. Определите ДВПВ  выходного сигнала и далее спектр входного сигнала . Далее найдите входной сигнал, используя обратное ДВПФ.

Ответ.  .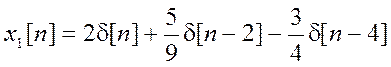

Указание.  Выразите входной сигнал,  как 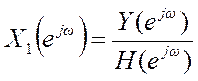   и найдите обратное ДВПФ.

7.  Найдите частотные характеристики системы с уравнением  

Ответ.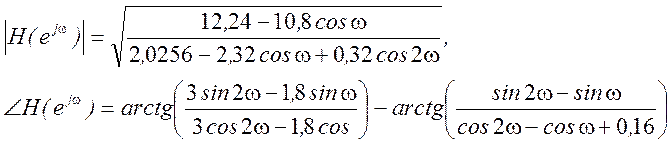 

8.  Заданы входной сигнал   и соответствующий выходной сигнал      линейной дискретной системы. Определите импульсную характеристику системы.

Указание.  Найдите передаточную функцию системы и определите импульсную характеристику как обратное Z- преобразование от передаточной функции.

Ответ.   .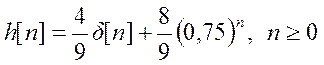

9.    На вход системы с уравнением    подаётся входной сигнал вида  при нулевых начальных условиях, u[n] – единичная ступенчатая функция. Определите выходной сигнал системы.

Ответ.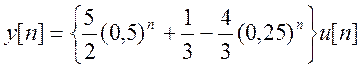  

10.    Постройте диаграмму нулей и полюсов системы с передаточной функцией
 .

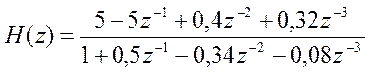Ответ.  .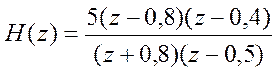

11.   Задана передаточная функция системы 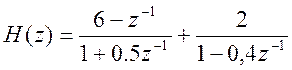 .  Определите её импульсную характеристику.

Ответ.  .

12.  На вход линейной дискретной системы с передаточной функцией

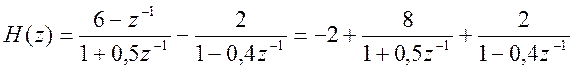
подается  сигнал  .  Найдите выходной сигнал  y[n].
Ответ.  .
Указание.  Определите  , разложите Y(z) на простейшие дроби и выполните обратное  Z – преобразование.

13.  Входной сигнал системы ,  при этом выходной сигнал 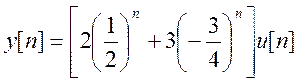 .    Найдите
а)  передаточную функцию системы,
б)  импульсную характеристику системы,
в)  разностное уравнение системы.
Ответ.   а)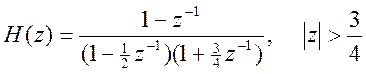 
               б)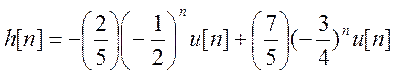  
                г)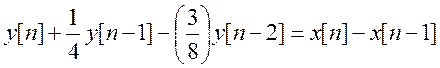   

14.     Определите  АЧХ   фильтра скользящего среднего с уравнением
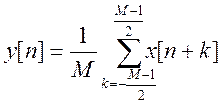 для  М = 7. Объясните физический смысл фильтра, основываясь на его частотной характеристике.

Ответ.  .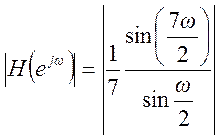

Составил      доц.   Щетинин Ю.И.