НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 5
ДИСКРЕТНОЕ И БЫСТРОЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Выполнили: Проверил:
Белых Мария Щетинин Ю.И.
Лысенко Татьяна
Группа: АО-21
Новосибирск2004
Цель работы:Изучение дискретного преобразования Фурье и его свойств, алгоритмов быстрого преобразования Фурье, приобретение практических навыков вычисления и использования дискретного преобразования Фурье в среде Matlab.
2. Используя функцию dftsum() для вычисления ДПФ по выражению (1)
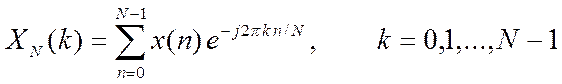 , (1)
, (1)
вычислить ДПФ и построить графики амплитудных спектров следующих сигналов:
а) ![]() для N = 10.
для N = 10.
а) x(n) = 1 для N = 10,
б) x(n) = cos(2πn/10) для N = 10.
Файл-сценарий для вычисления ДПФ дельта-функции и единичной функции.
N=10; % Число отчетов
n=0:1:N;
df=1; Fmax=5;
f=-Fmax:df:Fmax;
k=1:10;
g(k)=1;
g(k+1)=0;%Задаем дельта-функцию
y=dftsum(g);% Вычисление ДПФ
s(k)=1;%Задаем единичный сигнал
%s(k+1)=0;
y1=dftsum(s);y1p=fftshift(y1)./10;% Вычисление ДПФ
% Построение графиков сигналов и их амплитудных спектров
subplot(411), stem(n,g); title('Signal')
subplot(412), stem(f,abs(y)); title('Amplitude spectrum')
subplot(413), stem(n,s); title('Signal')
subplot(414), stem(f,abs(y1)); title('Amplitude spectrum')
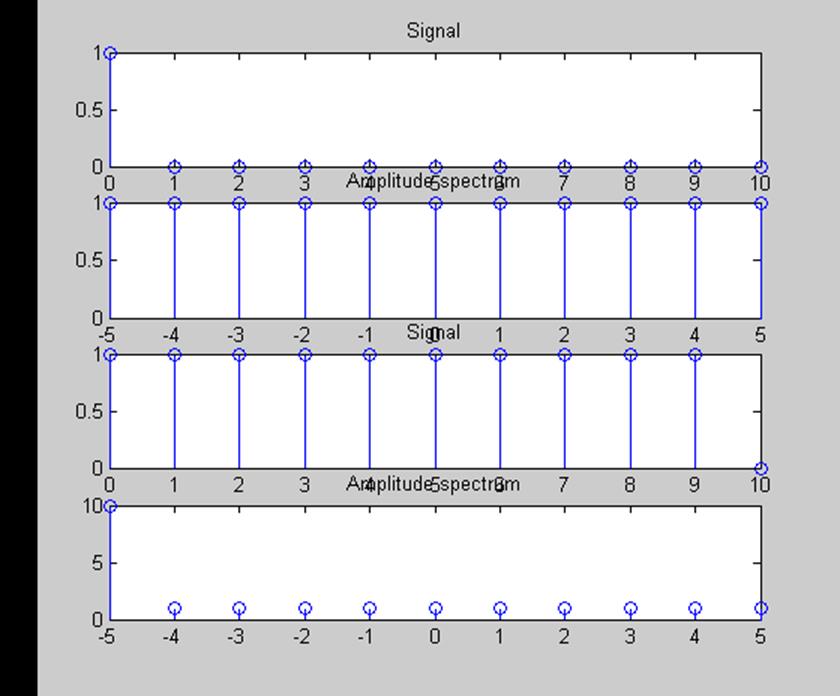
Рис.1 Графики дельта-функции и единичной функции и их амплитудных спектров
Файл-сценарий для вычисления ДПФ x(n) = cos(2πn/10) для N = 10
N=10; % Число отчетов
n=0:1:N;
df=1; Fmax=5;
f=-Fmax:df:Fmax;
x=cos(2*pi*n/10);; % задание сигнала
y1=dftsum(x); y1p=fftshift(y1)./10; % вычисление и сдвиг ДПФ
% Построение графика сигнала и его амплитудного спектра
figure(1), subplot(211), stem(n,x), title('Signal')
subplot(212), stem(f,abs(y1p)),title('Amplitude spectrum')
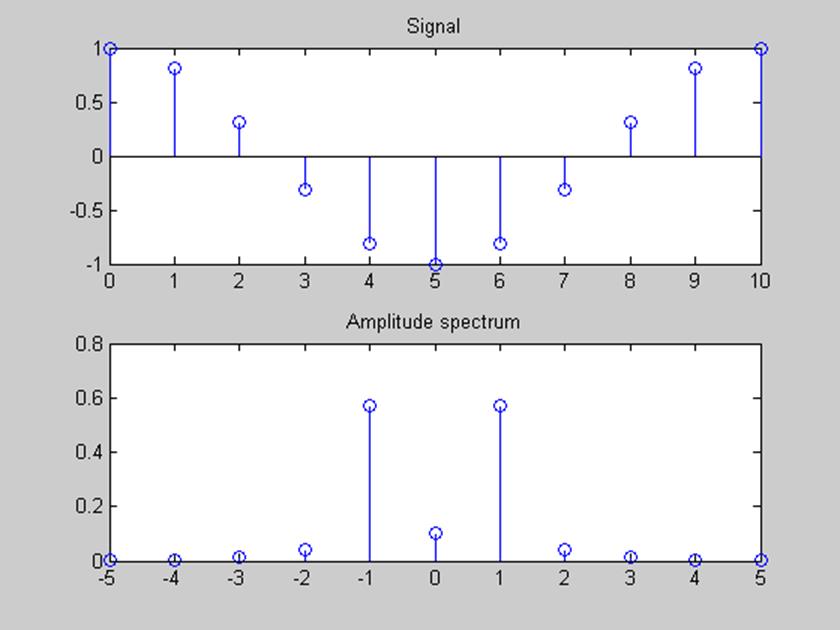
Рис.2 Графики функции x(n) = cos(2πn/10) и ее амплитудный спектр.
3. Написать Matlab-функцию для вычисления обратного (инверсного) ДПФ по выражению(2 )с форматом x = idftsum(X).
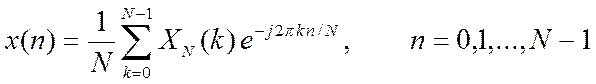 , (2)
, (2)
где X – N-точечный вектор ДПФ, x – вектор сигнала во временной области.
Применить функцию idftsum(X) для вычисления обратного ДПФ вышеприведенных сигналов. Сопоставить графики исходных сигналов и результаты вычисления с помощью idftsum(X).
Файл-функция для вычисления обратного ДПФ
function x=idftsum(X);
N=length(X);
for n=0:1:N-1;
for k=0:1:N-1;
Xk(k+1)=(X(k+1).*exp(j.*2.*pi.*k.*n./N))./10;
end;
x(n+1)=sum(Xk);
y=abs(x(n+1));
end;
Файл-сценарий вычисления обратного ДПФ для дельта-функции и единичной функции.
N=10; % Число отчетов
n=0:1:N;
k=1:10;
g(k)=1;
g(k+1)=0;%Задаем дельта-функцию
y=dftsum(g);% Вычисление ДПФ
y2=idftsum(y);% Вычисление обратного ДПФ
s(k)=1;%Задаем единичный сигнал
y1=dftsum(s);% Вычисление ДПФ
y3=idftsum(y1);% Вычисление обратного ДПФ
% Построение графиков исходных и полученных с помощью функции
% idftsum сигналов
subplot(411), stem(n,g); title('Delta-function')
subplot(412), stem(n,y2);
subplot(413), stem(n,s); title('Ones signal')
subplot(414), stem(n,y3);
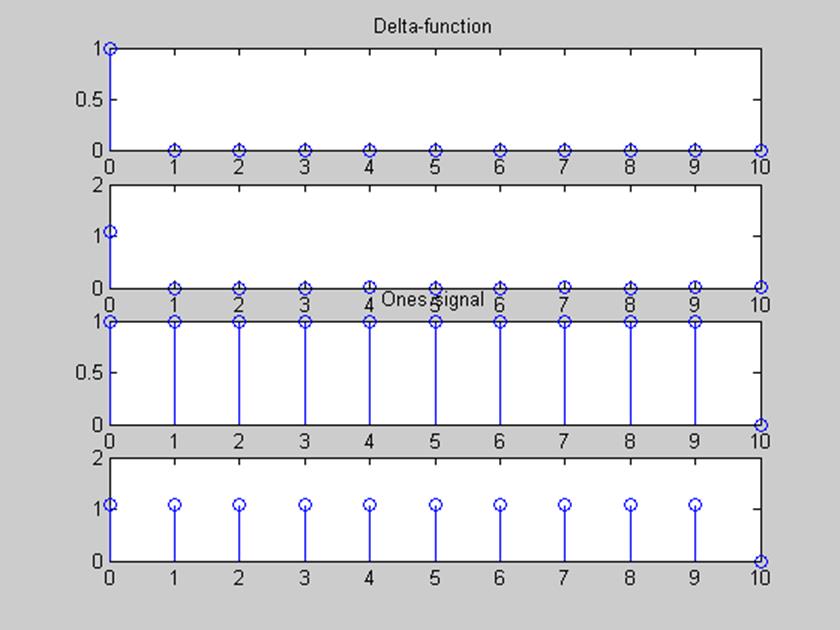
Рис.3 Графики исходных и полученных с помощью функции
idftsum сигналов дельта-функции и единичной функции
Файл-функция вычисления обратного ДПФ для последовательности ) x(n) = cos(2πn/10).
N=10; % Число отчетов
n=0:1:N;
x=cos(2*pi*n/10);; % задание сигнала
y=dftsum(x);% Вычисление ДПФ
h=idftsum(y);% Вычисление обратного ДПФ
% Построение графиков исходного и полученного с помощью функции
% idftsum сигналов
figure(1), subplot(211), stem(n,x)
subplot(212), stem(n,h)
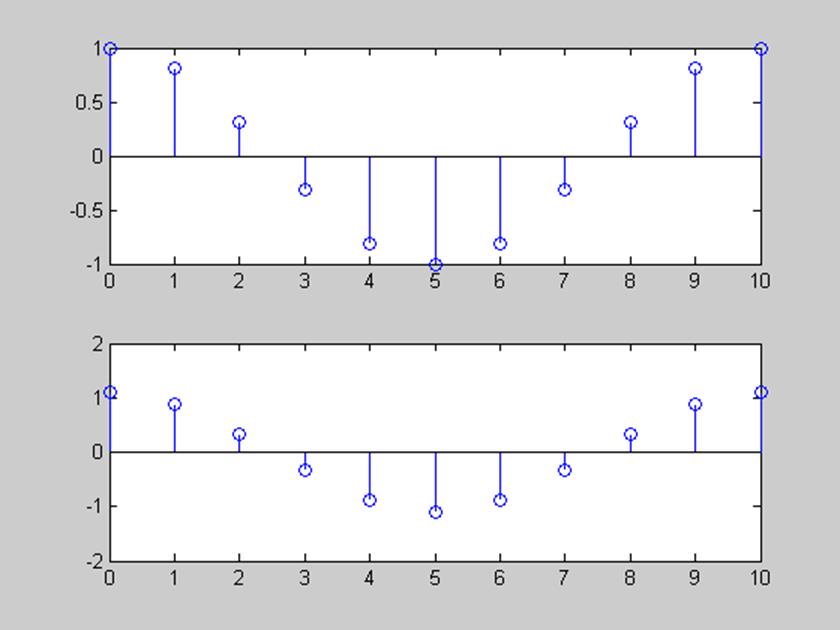
Рис.4 График исходного и полученного с помощью функции
Idftsum сигнала x(n) = cos(2πn/10
Вывод: Выполнив программу для вычисления ДПФ, мы построили графики амплитудных спектров заданных сигналов. Далее с помощью написанной нами файл-функции idftsum() вычислили обратное ДПФ используя полученные ранее (в п.2) результаты вычисления ДПФ. Построив графики исходных сигналов и вычисленных в п.3 мы убедились, что оно идентичны.
4. Вычислить с помощью функции dftsum(x) ДПФ случайной последовательности длиной 503 точки. Используя функцию randn()для генерирования последовательности и определить время вычисления функции dftsum(x) с помощью встроенной в Matlab процедуры cputime .
Файл-сценарий для определения времени вычисления ДПФ с использованием функции dftsum()
t=0:1:502;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
t2=cputime - t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
>> zad5_4
t2 =
0.4910 Время вычисления ДПФ
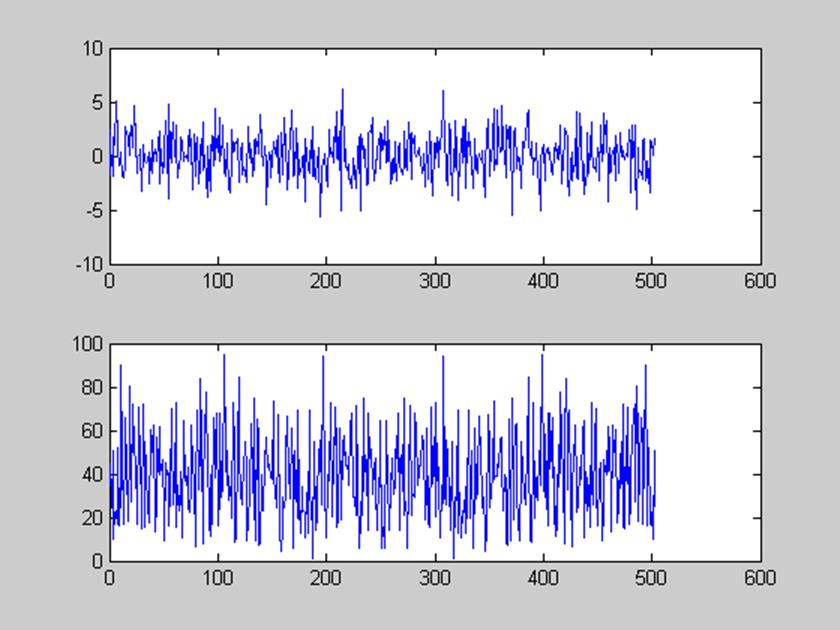
5.Вычислить ДПФ случайной последовательности длиной 503 точки с помощью встроенной в Matlab функции fft(). Определить (функция cputime) время вычисления ДПФ и сопоставить его с временем вычисления функции dftsum().
Файл-сценарий для определения времени вычисления ДПФ с использованием функции fft()
t=0:0.001:0.502;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=fft(x); % Вычисление ДПФ
t2=cputime - t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
>> zad5_5
t2 =
0.0200 Время вычисления ДПФ
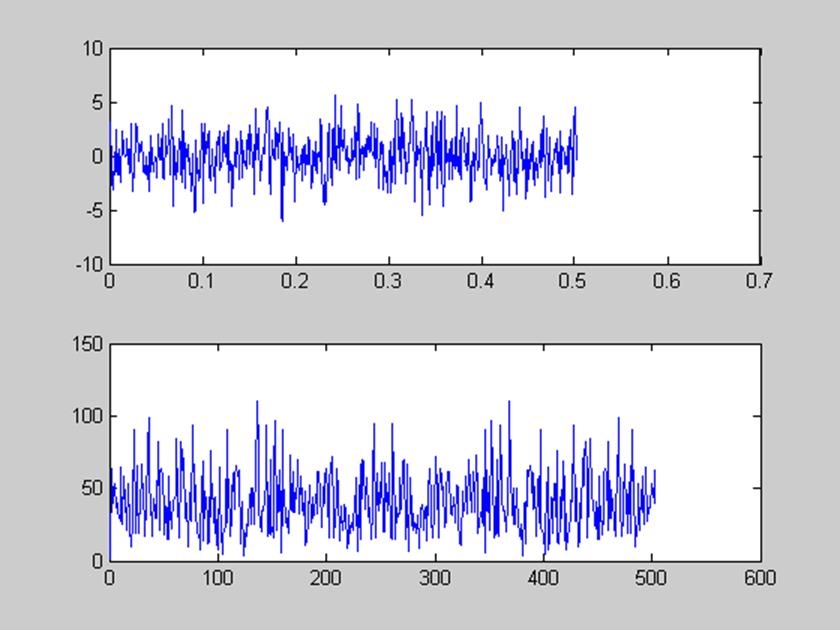
Вывод: Выполнив программу, предложенную нам в приложении1 мы определили время вычисления ДПФ с помощью функции dftsum() равное t=0,4910. Внеся в программу соответствующие изменения мы определили время вычисления ДПФ с помощью функции fft() равное t1=0,0200. Вычислив отношение t1/t=24.5 сделали вывод, что функция fft() быстрее определяет время вычисления ДПФ чем функция dftsum().
6.Определить ближайшее сверху
к значению 503 число, являющееся степенью 2. Найти время вычисления ДПФ для
последовательности такой длины с помощью функций dftsum() и fft(). При вычислении
с помощью fft() организовать
цикл из 1000 вычислений и разделить общее время вычисления цикла на 1000.
Объяснить различие времени вычисления для рассматриваемого случая по
сравнению с предшествующим пунктом работы.
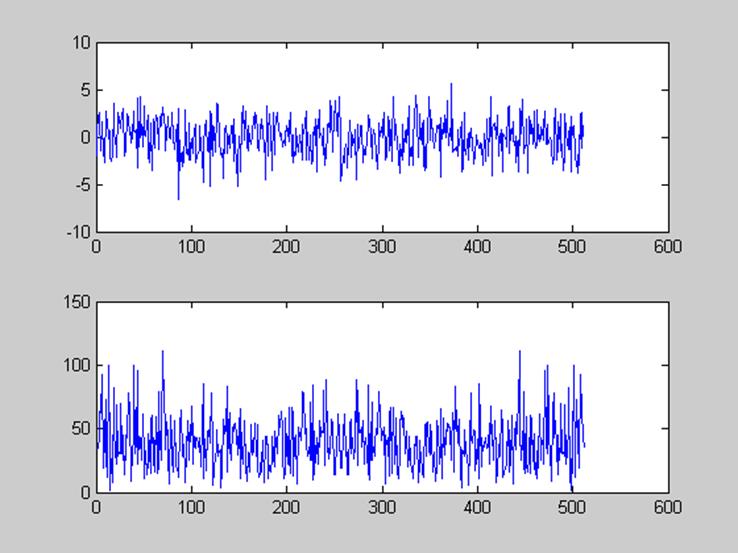
t=0:1:511;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
t2=cputime - t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
t2 =
0.5300
t=0:0.001:0.511;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
for k=0:1:1000;
y=k*fft(x);
end; % Вычисление ДПФ
t2=(cputime - t1)./1000 % Конец времени вычисления
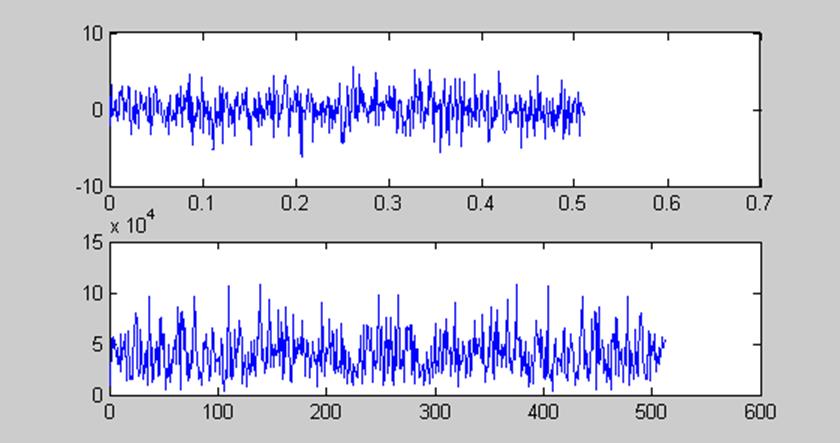
% Построение графиков во временной и частотной области
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
t2 =
1.5000e-004
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.