Вывод: Найдя время вычисления ДПФ для последовательности длины 512 отчетов с помощью функций dftsum() и fft() мы увидели, что для функции dftsum() время незначительно отличается от найденного в п. 4, а для функции fft() стало значительно меньше. Это связанно с тем, что число 512 является степенью 2.
7.Предполагая, что время
вычисления БПФ при основании 2 пропорционально 
(N – длина
последовательности), оцените время вычисления для последовательности длиной
4096 Определить действительное время вычисления БПФ длиной 4096, сопоставить с
оценкой времени. Чем можно объяснить различие?
В п. 6 мы нашли, что t=1.5*10-4 для нахождения коэффициента пропорциональности воспользуемся формулой: t=k*Nlog2N, выразив k получим: k=t/ Nlog2N. Подставим значения для t=1.5*10-4 и N=512 и получаем k=3,2*10-8. Получим теоретическое время вычисления БПФ длиной 4096: t_2= k*Nlog2N, получаем t_2=16*10-4 .
t=0:0.001:0.4096;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
for k=0:1:1000;
y=k*fft(x); % Вычисление ДПФ
end;
t2=(cputime - t1)./1000 % Конец времени вычисления
% Построение графиков во временной и частотной области
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
t2 =
1.8100e-004
Вывод: После выполнения соответствующей программы мы увидели, чтодействительное время вычисления БПФ длиной 4096 на порядок меньше теоретических ожиданий, это можно объяснить тем, что с ростом N уменьшается время вычисления БПФ.
8.Создайть две
последовательности длиной по 16 точек каждая
а)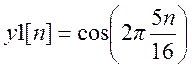 
, (3)
б) 
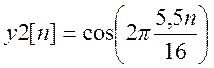. (4)
1) Вычислить ДПФ для обеих последовательностей и постройте графики
амплитудного спектра с использованием функции stem().
Файл-сценарий для построения графиков последовательностей (3) и (4) длинной 16 точек и их амплитудных спектров.
N=16; %Число отчетов
n=0:1:N-1;
K=(N-1)/2; k=-K:1:K;
% Формирование последовательностей
x1=cos(2*pi*5*n/16);
y1=fft(x1); % Вычисление ДПФ
x2=cos(2*pi*5.5*n/16);
y2=fft(x2); % Вычисление ДПФ
% Построение графиков сигналов и их амплитудных спектров
subplot(411), plot(n,x1), title('Signal 1')
subplot(412), stem(k,abs(y1)), title('Amplitude spectrum')
subplot(413), plot(n,x2), title('Signal 2')
subplot(414), stem(k,abs(y2)), title('Amplitude spectrum')
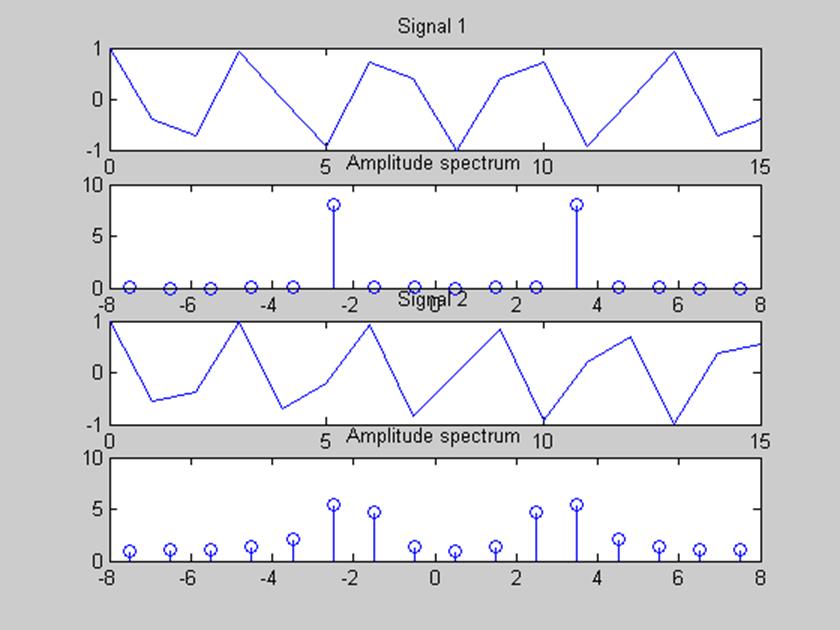
Рис.5 Графики сигналов (3) и (4) и их амплитудных спектров для N=16
2) Дополнить каждую из
последовательностей 48 точками из нулей до длины 64 точки и построить графики
амплитудного спектра для обеих последовательностей. Сравнить с предыдущими
графиками и объяснить различия в поведении.
Файл-сценарий для построения графиков амплитудных спектров последовательностей (3) и (4) дополненных нулями до длины 64 точки.
N=16; %Число отчетов
n=0:1:N-1;
K=(N-1)/2; k=-K:1:K;
N1=64;%Число отчетов
n1=-(N1-1)/2:1:(N1-1)/2;
x1=cos(2*pi*5*n/16);%Задаем первую последовательность
xx1=[x1,zeros(1,48)]; %Дополняем последовательность нулями
yy1=dftsum(xx1); % Вычисление ДПФ
x2=cos(2*pi*5.5*n/16);%Задаем вторую последовательность
xx2=[x2,zeros(1,48)];%Дополняем последовательность нулями
yy2=fft(xx2); % Вычисление ДПФ
% Построение графиков в амплитудных спектров
subplot(411), stem(k,abs(y1)), title('Amplitude spectrum for N=16')
subplot(412), stem(n1,abs(yy1)),title('Amplitude spectrum for N=64')
subplot(413), stem(k,abs(y2)), title('Amplitude spectrum for N=16')
subplot(414), stem(n1,abs(yy2)),title('Amplitude spectrum for N=64')
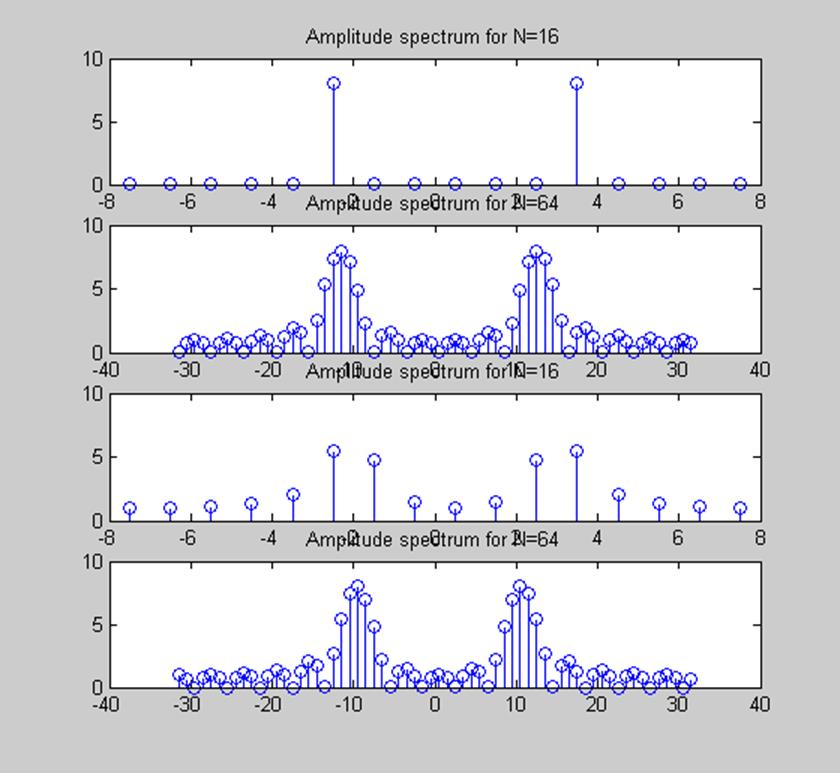
Рис.6 Графики сигналов (3) и (4) дополненные 48-ю нулями и их амплитудных спектров для N=64
3) Создать
последовательности косинусоидальных гармоник длиной
N = 64. Построить графики амплитудных спектров для
этого случая и сравнить с предшествующими результатами.
Файл-сценарий для построения графиков косинусоидальных последовательностей длинной 64 точки и их амплитудных спектров.
N=64; %Число отчетов
n=0:1:N-1;
K=(N-1)/2; k=-K:1:K;
% Формирование последовательностей
x1=cos(2*pi*5*n/16);
y1=fft(x1); % Вычисление ДПФ
x2=cos(2*pi*5.5*n/16);
y2=fft(x2); % Вычисление ДПФ
% Построение графиков сигналов и их амплитудных спектров
subplot(411), stem(n,x1), title('Signal 1')
subplot(412), stem(k,abs(y1)), title('Amplitude spectrum')
subplot(413), stem(n,x2), title('Signal 2')
subplot(414), stem(k,abs(y2)), title('Amplitude spectrum')
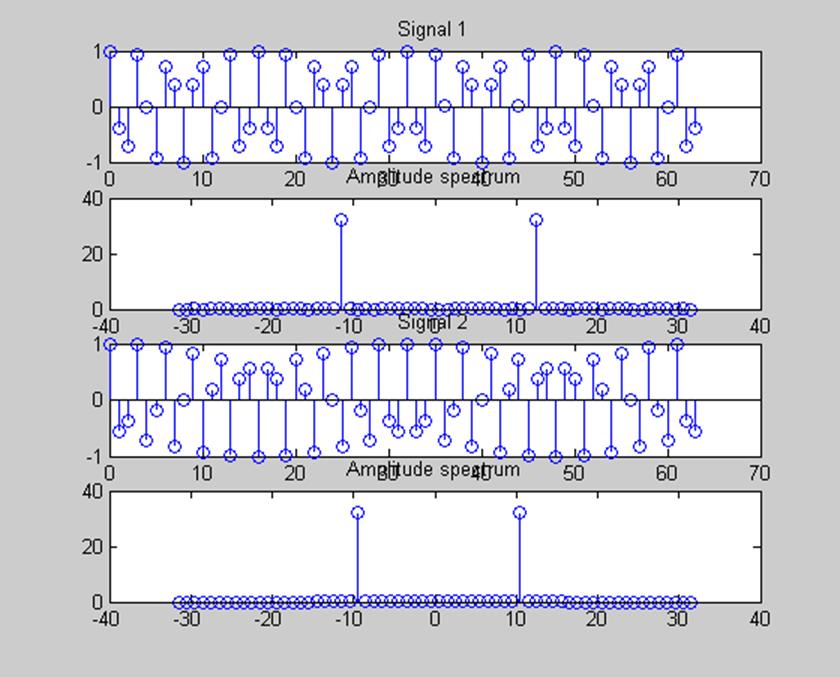
Рис.7 Графики косинусоидальных последовательностей длинной 64 точки и их амплитудных спектров.
Вывод: Сравнив графики, построенные по п.1) и 2) мы видим, что при дополнении последовательностей (3) и (4) нулями амплитудные спектры этих сигналов стали более ????подробными?????.
9.Сгенерировать экспоненциальный дискретный сигнал длительностью 100 отсчетов и прямоугольный сигнал из 40 отсчетов.
1)Выполнить дискретную свертку этих сигналов (функция conv) и представить её график. Далее выполнить свертку этих сигналов с помощью БПФ (круговая свертка). Постройте график модуля и сравните с результатами, полученными функцией conv(), прокомментировать особенности и преимущества вычисления свертки с использованием ДПФ.
Файл-сценарий построения графика дискретной свертки
N1=100;
n1=0:0.01:N1/100;
% Формирование экспоненциального сигнала
x1=exp(n1);
N2=40;
n2=- N2/20:0.01:N2/20;
% Формирование прямоугольного сигнала
x2=rectpuls(n2);
Y=conv(x1,x2);%Свертка
% Построение графиков сигналов и их свертки свертки
subplot(411), stem(n1,x1)
subplot(412), stem(n2,x2)
subplot(413), stem(Y)
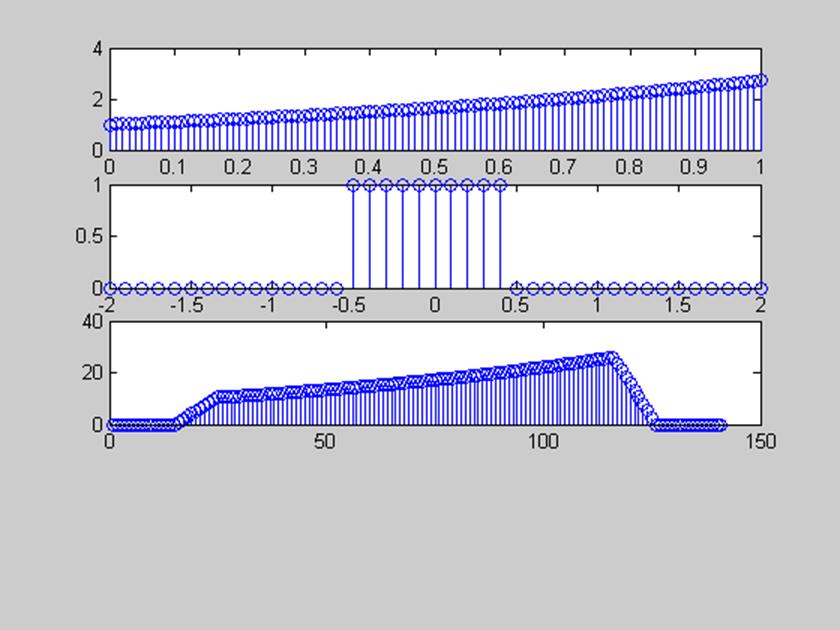
2)Выполнить свертку этих сигналов с помощью БПФ (круговая свертка). Постройте график модуля и сравните с результатами, полученными функцией conv(), прокомментировать особенности и преимущества вычисления свертки с использованием ДПФ.
Файл-сценарий построения графиков дискретной и круговой свертки
N1=100;
n1=0:0.01:(N1-1)./100;
% Формирование экспоненциального сигнала
x1=exp(n1);
X1=[x1 zeros(1,156)];
y1=fft(X1);
N2=40;
n2=-(N2-1)./20:0.1:(N2-1)./20;
% Формирование прямоугольного сигнала
x2=rectpuls(n2);
X2=[x2 zeros(1,216)];
y2=fft(X2);
Y=y1.*y2;
N=256;
n=0:1:N-1;
YY=ifft(Y);% Круговая свертка
Y=conv(x1,x2);%Дискретная свертка
% Построение графиков свертки
subplot(211), stem(Y)
subplot(212), stem(n,abs(YY))
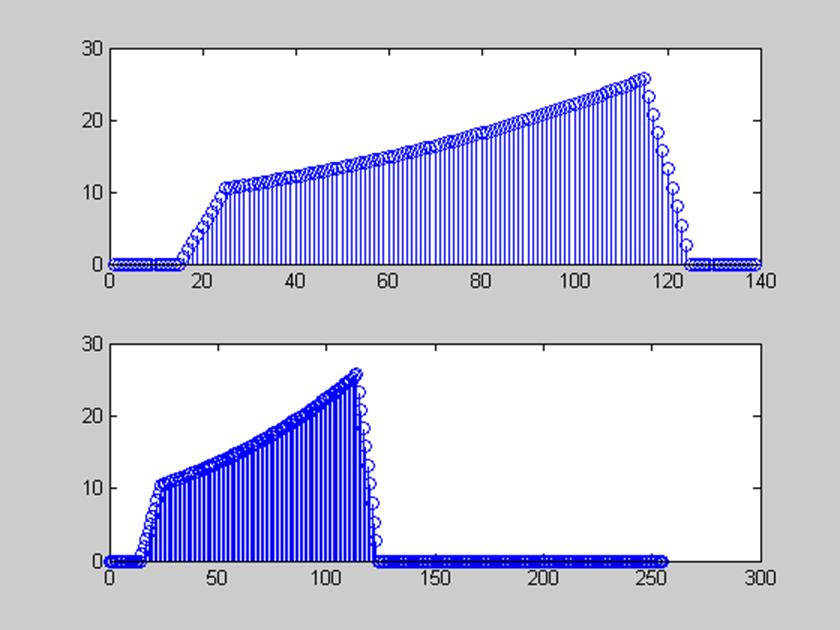
Рис.8 Графики дискретной и круговой свертки
10.Выполнить пример использования преобразования Фурье для выделения полезного сигнала из смеси с шумом. Построить график этого сигнала во временной области.
Вычислить спектральную
плотность мощности (СПМ) сигнала по выражениям
y = fft(y,512)
pyy=y.*conj(y)/512
% вычисление СПМ
Построить график СПМ. Объясните результаты.
Файл-сценарий построения графиков в задаче выделения гармонических сигналов из смеси с шумом
t=0:0.001:0.6;
x=sin(2*pi*50*t)+sin(2*pi*100*t);
y1=x+2*randn(size(t));
subplot(211), plot(y1(1:100)), grid
title('График зашумленного сигнала')
y=fft(y1,512);
pyy=y.*conj(y)/512;
f=1000*(0:255)/512;
subplot(212), plot(f, pyy(1:256)),grid
title('График спектра мощности')
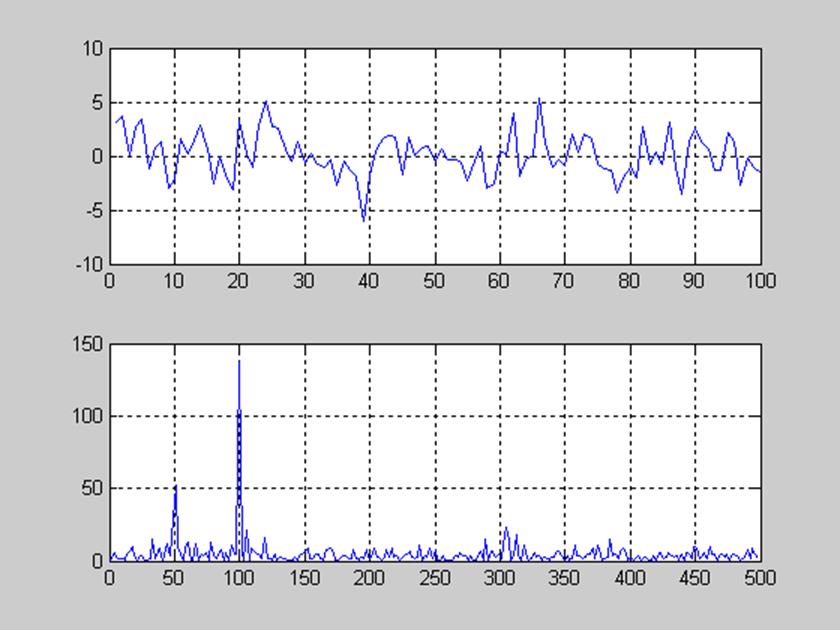
Рис.9 Графики выделения гармонических сигналов из смеси с шумом.
Вывод: После выполнения программы, предложенной нам в приложении2, которая является примером использования преобразования Фурье для выделения полезного сигнала из смеси с шумом по графику рис.9 убедились, что полученные графики не позволяют определить, какие частоты присутствуют в рассматриваемом сигнале.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.