Министерство Образования и Науки РФ
Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра Систем Сбора и Обработки Данных
«Теория и обработка сигналов»
Лабораторная работа № 9
«Z - преобразование
и дискретно – временное преобразование Фурье»
Вариант 7
Группа: АТ-93 Преподаватель: доц. Щетинин Ю.И.
Студент: Кириллова М.А.
Новосибирск - 2012
Цель работы: изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
1. Определение Z – преобразований и областей сходимости заданных сигналов аналитически.
Прямое Z – преобразование сигнала определяется по выражению:
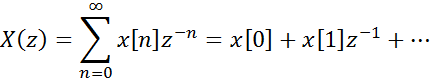
Где![]() -
комплексная переменная (частота),
-
комплексная переменная (частота),
![]() –
значения отсчёты) сигнала.
–
значения отсчёты) сигнала.
Z-преобразование это степенной ряд от переменной ![]() или
или![]() ,
который ставит в соответствие последовательности
,
который ставит в соответствие последовательности ![]() функцию
функцию
![]() комплексной
переменной
комплексной
переменной ![]() .
.
Так как две
различные последовательности ![]() и
и
![]() могут
иметь одно и то же Z- преобразование, но различные
области сходимости, то во избежание появления ошибок следует рассматривать Z - преобразование вместе с его
областью сходимости.
могут
иметь одно и то же Z- преобразование, но различные
области сходимости, то во избежание появления ошибок следует рассматривать Z - преобразование вместе с его
областью сходимости.
Определим Z-преобразования и области сходимости для следующих сигналов:
a)
![]()
Z-преобразование единичного импульса ![]() :
:
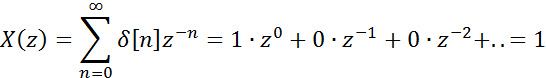
Областью
сходимости является вся ![]() -плоскость.
-плоскость.
b)
![]()
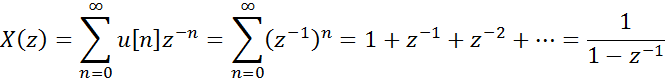
Сумма геометрической прогрессии равна
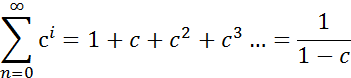
если ![]() . Следовательно,
. Следовательно, ![]() ,
, ![]() ,
,
![]() .
.
Значит область
сходимости – внешность окружности единичного радиуса ![]() .
.
c)
![]()
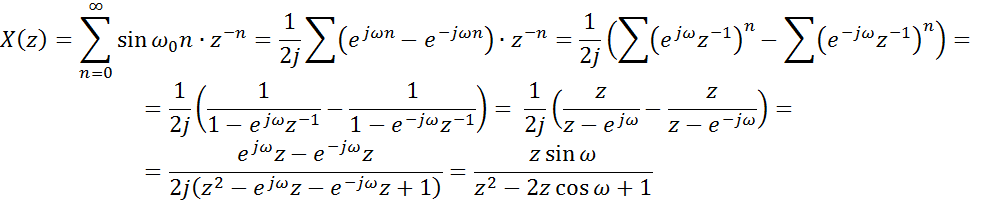
Полюса![]() :
:
![]()
Область
сходимости – внешность круга с радиусом ![]() ,
где
,
где ![]() -
полюс
-
полюс ![]() с максимальным модулем. Следовательно, в данном случае область
сходимости
с максимальным модулем. Следовательно, в данном случае область
сходимости ![]() .
.
d)
![]()
Используя теорему дифференцирования в ![]() – области
(умножения на
– области
(умножения на ![]() во временной области)
во временной области)
![]() и
то, что
и
то, что ![]() ,
получим:
,
получим:
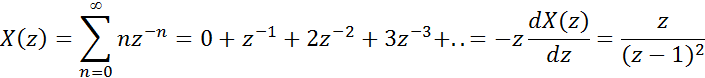
Функция имеет
полюс ![]() .
Следовательно, это Z– преобразование сходится во всех
точках за пределами круга с радиусом 1, в пределах круга она расходиться.
.
Следовательно, это Z– преобразование сходится во всех
точках за пределами круга с радиусом 1, в пределах круга она расходиться.
2. Определение Z – преобразований заданных сигналов с помощью функции ztrans().
В Matlab для определения Z-преобразований сигналов используется функция ztrans().
Воспользуемся данной функцией для нахождения Z-преобразований следующих сигналов.
a)
![]()
Для нахождения Z-преобразования воспользуемся следующей последовательностью команд:
syms a w n
x=((a^n)*cos(w*n));
X=ztrans(x)
X = (z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
Запишем данное выражение в обычной математической форме (5).
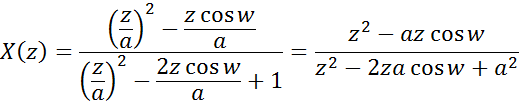
b)
![]()
Для нахождения Z-преобразования воспользуемся следующей последовательностью команд.
syms n
x=(n^2)*exp(2*n);
X=ztrans(x)
X = z*exp(2)*(z+exp(2))/(z-exp(2))^3.
Запишем данное выражение в обычной математической форме (6).
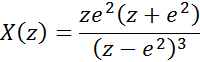
c)
![]()
Для нахождения Z-преобразования воспользуемся следующей последовательностью команд:
syms n
x=((cos(n))^2);
X=ztrans(x)
X= z*(z^2-3*z*cos(1)^2+z+cos(1)^2)/(z^3-4*z^2*cos(1)^2+z^2+ +4*z*cos(1)^2-z-1)
Запишем данное выражение в обычной математической форме:
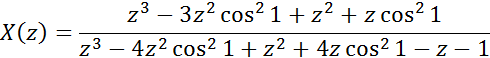
3. Определение сигналов по их Z – преобразованиям с помощью функции iztrans().
В Matlab для определения исходных сигналов по их Z – преобразованиям используется функция iztrans(). Воспользуемся данной функцией для нахождения оригиналов следующих сигналов:
a)
![]()
Для нахождения исходного сигнала по его Z-преобразованию воспользуемся следующей последовательностью команд:
syms z;
X=z*(z+1)/(z-1)^3;
x=iztrans(X)
x =n^2.
Запишем данное выражение в обычной математической форме:
![]()
b)
![]()
Для нахождения исходного сигнала по его Z-преобразованию воспользуемся следующей последовательностью команд:
syms z
X=((z^2-0.2*z-0.8)/(z^2-0.3*z-0.1));
x=iztrans(X)
x = 8*charfcn[0](n)-13/7*(1/2)^n-36/7*(-1/5)^n
Запишем данное выражение в обычной математической форме:
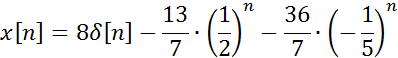
Функции ztrans()и iztrans() нужны для нахождения символьного прямого и обратного z-преобразования соответственно. Для выполнения этих функций и получения результата необходимо предварительно объявить все символьные переменные, затем передать нужное выражение в качестве аргумента, функции выведут результат в символьном виде. Так как вычислительные возможности этих функций ограничены, они чаще всего используются как обучающие вычислению прямого и обратного z-преобразования функции в среде Matlab.
4. Аналитическое определение обратного Z – преобразования, используя разложение рационального Z – преобразования на простые дроби.
Для определения обратного Z – преобразования разложим функцию рационального
Z – преобразования
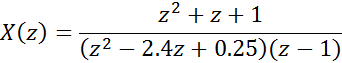
на простые дроби с помощью функции residuez().
Для этого используем следующую последовательность команд:
num=[0 1 1 1 ];
den=[1 -3.4 2.65 -0.25];
[r, p, k]=residuez(num,den)
Получим
r = p =
1.3235 2.2909
-2.6087 1.0000
5.2852 0.1091
k = -4
На основе полученных значений запишем разложение исходного выражения на простые дроби.
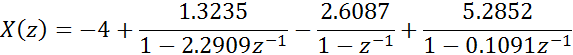
Используя полученное разложение, найдём аналитически обратное Z - преобразование.
Так как ![]()
![]()
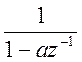 , то
, то ![]()
![]()
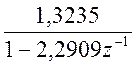 ,
,
![]()
![]()
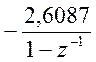 ,
, ![]()
![]()
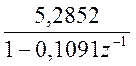 .
.
Так как ![]() , то
, то ![]()
![]()
![]() .
.
Таким образом, получили обратное Z – преобразование (*).
![]()
Для проверки полученного результата воспользуемся функцией iztrans().
syms z;
X= -4+1.32/(1-2.29*z^(-1))-2.6/(1-z^(-1))+5.28/(1-0.11*z^(-1));
iztrans(X)
В результате получим
ans = -4*charfcn[0](n)+33/25*(229/100)^n-13/5+132/25*(11/100)^n
Переписав данное
выражение, получим функцию ![]() в виде :
в виде :
![]()
Решение (*), найденное аналитически совпадает с точностью до погрешности вычислений с последним выражением, определённым с помощью Matlab.
5. Решение линейного разностного уравнения с постоянными коэффициентами с помощью Z– преобразования.
С помощью Z-преобразования решим линейное разностное уравнение с постоянными коэффициентами:
![]()
Беря Z- преобразование от этого уравнения, пользуясь свойствами линейности и временного сдвига, получим.
![]()
Преобразовав полученное выражение,
учитывая начальные условия ![]() и подставляя
выражение Z – преобразования входного сигнала
и подставляя
выражение Z – преобразования входного сигнала 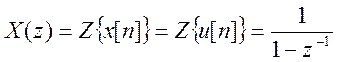 , получим линейное алгебраическое
уравнение:
, получим линейное алгебраическое
уравнение: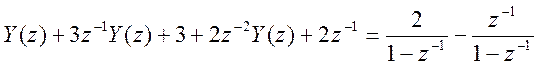 , решив которое получим:
, решив которое получим:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.