Изучение Z-преобразования и дискретно- временного преобразования Фурье. Вариант 7, страница 3

Докажем данное свойство.

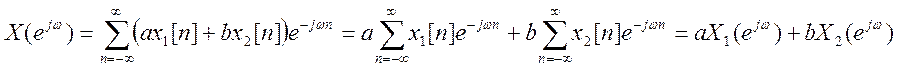
Значит, .

Следующий script-файл иллюстрирует свойство линейности ДВПФ.

% Свойство линейности

alpha = 0.5;

beta = 0.25;

y = alpha*g+beta*h;

[Y,w] = DTFT(y,512);

% Графики Y и  alpha*G+beta*H для проверки их равенства

figure(3), subplot(211),plot(w,abs(Y))

title('Амплитудный спектр, найденный как DTFT(alpha*g+beta*h)')

subplot(212), plot(w,abs(alpha*G+beta*H))

Результат представлен на рис. 6.

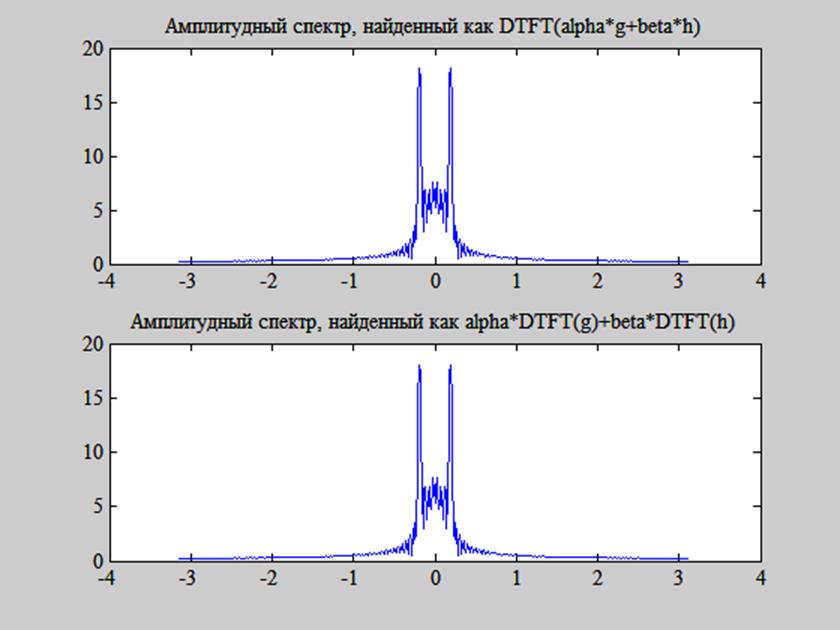
Рис. 6. Иллюстрация свойства линейности ДВПФ.

На рис.6 видим, что графики амплитудных спектров, полученных, как сумма ДВПФ сигналов и как ДВПФ суммы тех же сигналов совпадают, значит, свойство линейности выполняется.

8.2.  Свойство временного сдвига.

Если   , то .

Докажем данное свойство.

ДВПФ – частный случай Z – преобразования при . Поэтому докажем свойство временного сдвига для Z – преобразования

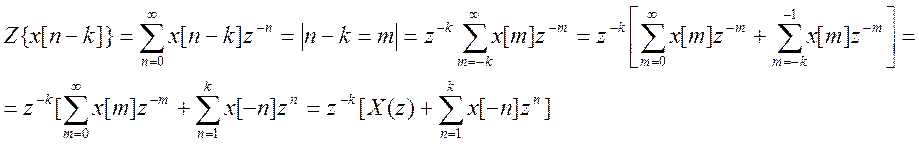
Получили .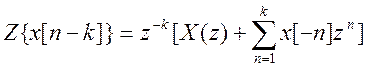

Сделав замену, получим свойство временного сдвига для ДВПФ.

Следующий script-файл иллюстрирует свойство временного сдвига ДВПФ.

% Свойство временного сдвига

n0 = 12;

% y2 - последовательность y, сдвинутая на 12 отсчетов

y2 = [zeros([1,n0]) g];

[Y2,w] = DTFT(y2,512);

G0 = exp(-j*w*n0).*G;

% Графики амплитудных спектров

figure(3), subplot(211), plot(w,abs(G0))

title('Амплитудный спектр, найденный как exp(-j*w*n0)*DTFT(g)')

subplot(212), plot(w,abs(Y2));

title('Амплитудный спектр, найденный как DTFT(g[k-n0])')

Результат представлен на рис. 7.

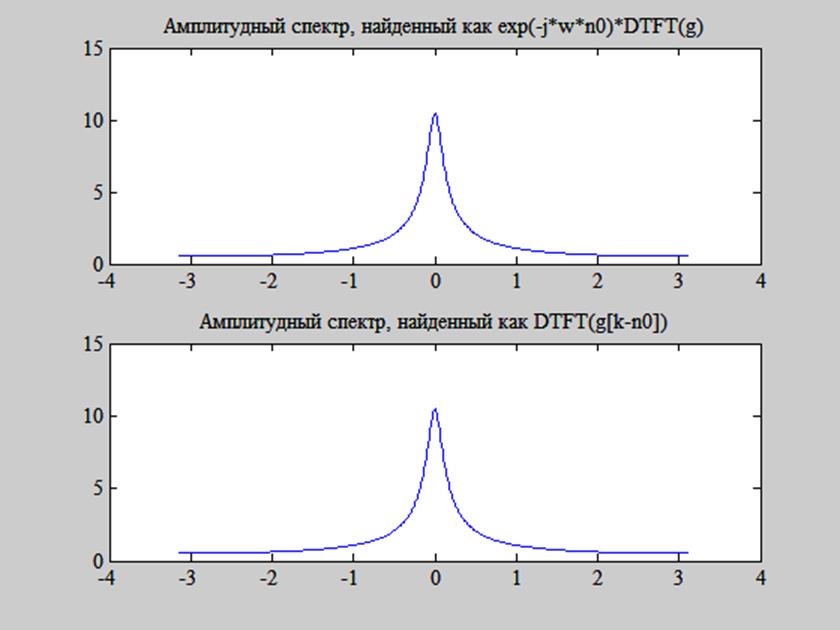
Рис. 7. Иллюстрация свойства временного сдвига ДВПФ.

На рис. 7 видим, что график амплитудного спектра сигнала, полученный через определение ДВПФ сдвинутого на  сигнала, совпадает с графиком амплитудного спектра, полученным умножением исходного сигнала на . Значит, свойство временного сдвига выполняется.

8.3.  Свойство изменения масштаба.

Если   , то .

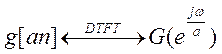Докажем данное свойство.

Следующий script-файл иллюстрирует свойство изменения масштаба ДВПФ.

% Свойство изменения масштаба

a=0.1;  % Коэффициент изменения масштаба

g1= exp(gamma*k*a);

[G,w] = DTFT(g,512);

G1 = DTFT(g1,512);

figure(4)

subplot(311), plot(k,g,k,g1)

title('Графики во временной области')

legend('g[k]','g1[k]')

subplot(312), plot(w,abs(G))

title('График амплитудного спектра сигнала g[k]')

subplot(313), plot(w,abs(G1))

title('График амплитудного спектра сигнала g1[k]')

Результат представлен на рис. 8.

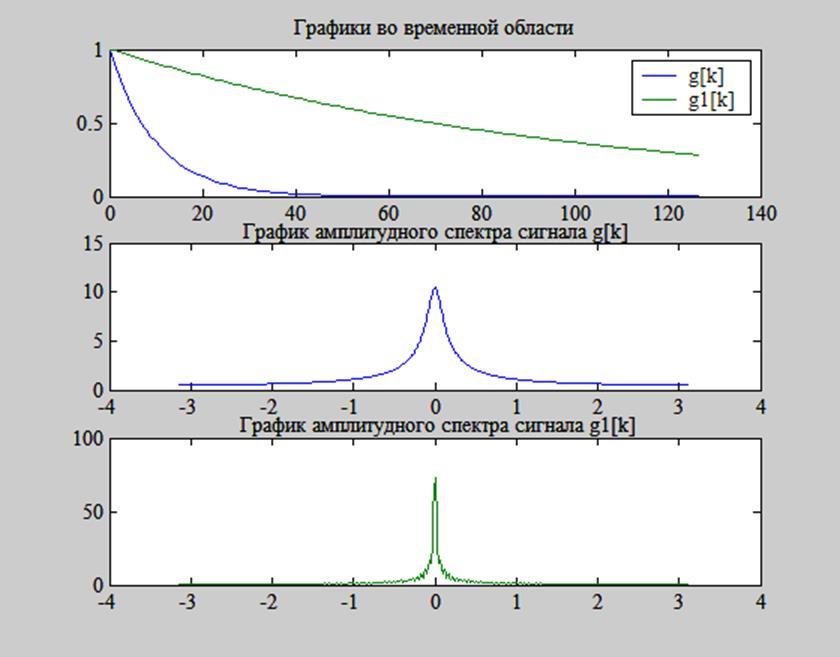
Рис. 8. Графики исходного и масштабированного сигналов и их амплитудных спектров.

На рис. 8 видим, что при коэффициенте масштабирования a = 0.1 g[ak] представляет собой функцию g[k], растянутую во времени в 10 раз. При этом амплитудный спектр сужается в 10 раз по оси частот. Чем шире сигнал по оси времени, тем уже его амплитудный спектр и наоборот. Таким образом, свойство изменения масштаба выполняется.

8.4.  Свойство свёртки.

Если    и , то

.                                                                                     (29)

Докажем данное свойство.

ДВПФ – частный случай Z – преобразования при . Поэтому докажем свойство свёртки для Z – преобразования

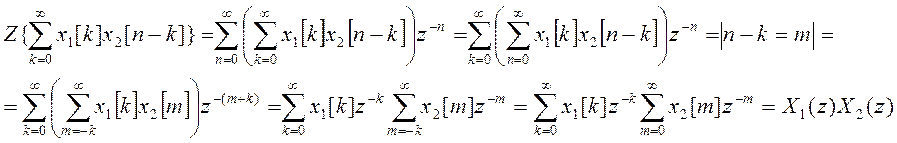
Получили .

Сделав замену, получим свойство свёртки для ДВПФ.

Следующий script-файл иллюстрирует свойство свёртки ДВПФ.

% Свойство свертки

y5 = conv(g,h);

[Y5,w] = DTFT(y5,512);

figure(6), subplot(211), plot(w,abs(Y5))

title('Амплитудный спектр свёртки DTFT(conv(g[k],h[k]))')

subplot(212), plot(w,abs(G.*H))

title('Амплитудный спектр DTFT(g[k])*DTFT(n[k]) ')

Результат представлен на рис. 9.

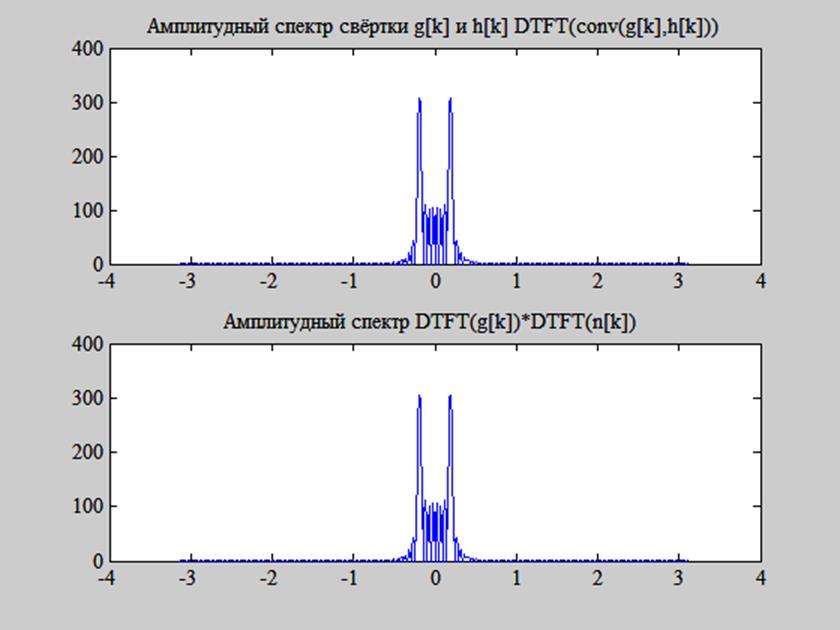
Рис. 9. Иллюстрация свойства свёртки ДВПФ.

На рис. 9 видим, что спектр свёртки сигналов g[k] и h[k], найденный непосредственным выполнением операции свёртки и последующим определением ДВПФ, совпадает со спектром, найденным как произведение ДВПФ сигналов g[k] и h[k]. Значит, свойство свёртки выполняется и свёртке во временной области соответствует произведение ДВПФ в частотной.

8.5.  Теорема Парсеваля.

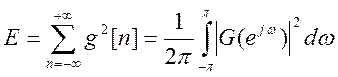Если   , то                                             (30)

Следующий script-файл иллюстрирует теорему Парсеваля для ДВПФ.

% Теорема Парсеваля

val1 = sum(g.*g);

val2 = sum(G.*conj(G))/512;

% Сравнение val1 с  val2

disp('Разность   val1-val2 = ')

disp(val1-val2)

В результате выполнения данного script-файла получили разность между 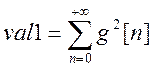 и 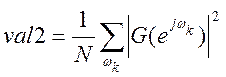 равную . Значение  пренебрежимо мало, значит, теорема Парсеваля выполняется и энергия  сигнала может быть найдена, как квадрат модуля ДВПФ данного сигнала.

Выводы:

1.  Для анализа дискретных и цифровых систем используется Z – преобразование, которое определяется по выражению

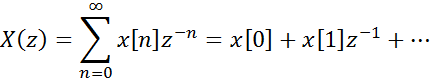
Где - комплексная переменная (частота),

 – значения отсчёты) сигнала.

В Matlab для определения Z – преобразований используется функция ztrans().

2.  Для перехода из области комплексной переменной z во временную (для получения дискретного сигнала – последовательности  по его Z - изображению) используется обратное Z – преобразование вида

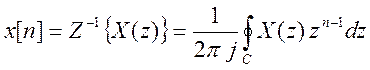
В Matlab для определения обратного Z – преобразования используется функция iztrans().

3.  Один из способов вычисления обратного Z – преобразования – использование разложения Z – изображения на простейшие (элементарные) дроби. Этот метод используется в тех случаях, когда вычисление интеграла, требуемое для определения обратного Z – преобразования, затруднительно.

В Matlab для разложения функции рационального Z – преобразования на простые используют функцию residuez().

4.  Z – преобразование используется для решения линейных разностных уравнений с постоянными коэффициентами. Решение заключается в определении Z – преобразования от уравнения (при этом используются свойства линейности и временного сдвига), нахождении решения в области комплексной переменной z и последующем переходе обратно во временную область.

Свойство линейности: ;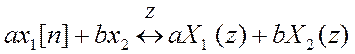

Свойство временного сдвига: а);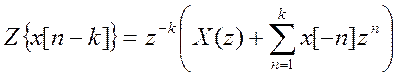

5.  Частным случаем Z – преобразования является ДВПФ (Z – преобразованием на единичной окружности, т.е.  при  )

Выражения анализа и синтеза имеют вид

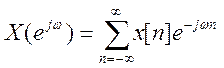            и          .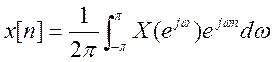

6.  ДВПФ обладает такими же свойствами, что и Z – преобразование.

Среди них свойство линейности, временного сдвига, изменения масштаба, свёртки, теорема Парсеваля.

7.