Министерство образования и науки РФ
Новосибирский Государственный Технический Университет
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 6-й семестр
Отчет
ПО ЛАБОРАТОРНОЙ РАБОТЕ №8
«Z - преобразование
и дискретно – временное преобразование Фурье»
Факультет: АВТ
Группа: АО-61
Вариант: 9
Студенты: Горлов А. Преподаватель: Доц. Щетинин Ю.И.
Пономаренко Ю.
Новосибирск, 2009
Цель работы: Изучение Z – преобразования и дискретно – временного преобразования Фурье (ДВПФ), их вычисления в среде Matlab.
Исходные данные:
1.
Индивидуальное
задание к п.5 для разложения на простые дроби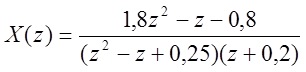
2.
Индивидуальное
задание к п.6 для получения навыков решения разностных уравнений с постоянными
коэффициентами с помощью Z-преобразования
![]()
1. Нахождение Z-преобразования аналитическим методом для следующих выражений:
а) x[n] = δ[n],
б) x[n] = u[n],
в) x[n] = cosωn.
Прямое одностороннее Z-преобразование: 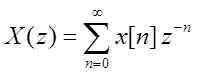 , где
, где ![]() - комплексная переменная,
- комплексная переменная, ![]() - функция дискретного сигнала, n – число отсчетов. Таким образом, Z-преобразование - степенной ряд от z-1, который ставит в соответствие
функции x[n] функцию комплексной переменной X(z). Используется как инструмент анализа дискретных и
цифровых систем.
- функция дискретного сигнала, n – число отсчетов. Таким образом, Z-преобразование - степенной ряд от z-1, который ставит в соответствие
функции x[n] функцию комплексной переменной X(z). Используется как инструмент анализа дискретных и
цифровых систем.
Обратное Z-преобразование:
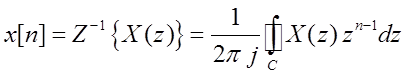 , где X(z) – функция комплексной переменной z,
, где X(z) – функция комплексной переменной z, 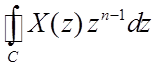 - интеграл по замкнутому контуру С,
который охватывает все особые точки (полюса) X(z). Используется для получения дискретного сигнала
- интеграл по замкнутому контуру С,
который охватывает все особые точки (полюса) X(z). Используется для получения дискретного сигнала ![]() по его Z-преобразованию.
по его Z-преобразованию.
a) x[n] = δ[n]
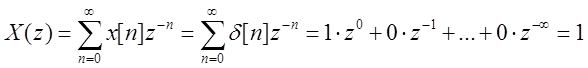
b) x[n] = u[n]
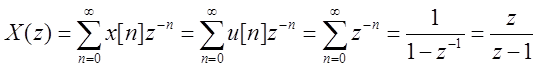
c) x[n] = cos ωn
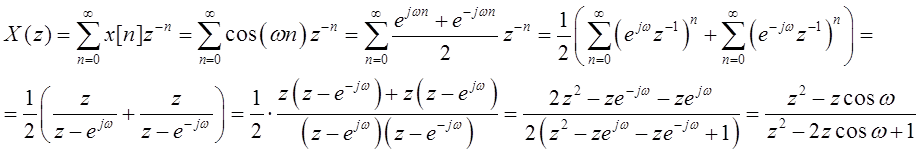
2. Нахождение Z-преобразования для следующих выражений cпомощью функции ztrans() Matlab:
а) x[n] = an cos ωn
б) x[n] = n2 e2n
в) x[n]=cos2n
а) x[n] = an cos ωn
% нахождение прямого z-преобразования
>> syms X x a w n
>> x=(a^n)*cos(w*n)
>> X=ztrans(x)
X = (z/a-cos(w))*z/a/(z^2/a^2-2*z/a*cos(w)+1)
б) x[n] = n2 e2n
% нахождение прямого z-преобразования
>> syms X x r w0 n e
>> x=n^2*e^(2*n);
>> X=ztrans(x)
X = -z*e^2*(z+e^2)/(-z+e^2)^3
в) x[n]=cos2n
% нахождение прямого z-преобразования
>> syms X x r w0 n e
>> x=(cos(n)).^2;
>> X=ztrans(x)
X = z*(z^2+z-3*z*cos(1)^2+cos(1)^2)/(z^3-4*z^2*cos(1)^2+z^2+4*z*cos(1)^2-z-1)
3. Нахождение обратного Z-преобразования для следующих выражений c помощью функции iztrans() Matlab:
а) 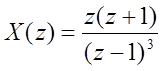 ,
,
б)
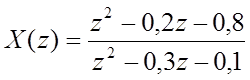 .
.
а) 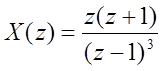
% нахождение обратного z-преобразования
>> syms z x X
>> X=(z*(z+1))/((z-1)^3);
>> x=iztrans(X)
x = n^2
б) 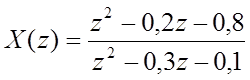
% нахождение обратного z-преобразования
syms z x X
>> X=((z^2)-0.2*z-0.8)/((z^2)-0.3*z-0.1);
>> x=iztrans(X)
x = 8*charfcn[0](n)-13/7*(1/2)^n-36/7*(-1/5)^n
4. Разложение функции (индивидуальное задание) на простые дроби с помощью функции residuez() и нахождение для нее обратного Z – преобразование аналитически и методами Matlab.
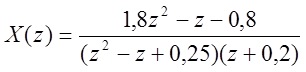
% разложение функции на простые дроби
>> num=[-0.8,-1,1.8];
>> den=[0.05,0.05,-0.8,1];
>> [r,p,k]=residuez(num, den)
r =
-5.3878
-5.7551 - 0.0000i
-4.8571 + 0.0000i
p =
-5.0000
2.0000 + 0.0000i
2.0000 - 0.0000i
k = -16
Полученному результату отвечает разложение на простые дроби вида
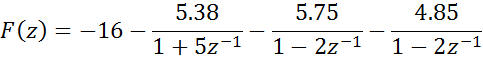
Откуда получаем исходный сигнал :
![]()
Сравним его с результатом выполнения функции iztrans():
>>syms x X z
>>X=((1.8*z^2)-z-0.8)/(((z^2)-z+0.25)*(z+0.2))
>>x=iztrans(X)
x = -(282*(2)^n)/49 - (264*(-5)^n)/49 - 16* charfcn[0](n) - (34*(2)^n)/7
5. Решение с помощью Z – преобразования линейного разностного уравнения с постоянными коэффициентами (индивидуальное задание)
![]() ;
; ![]() ;
; ![]()
![]()
![]()
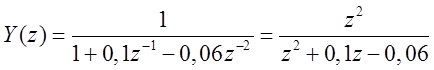
Полюса:
![]()
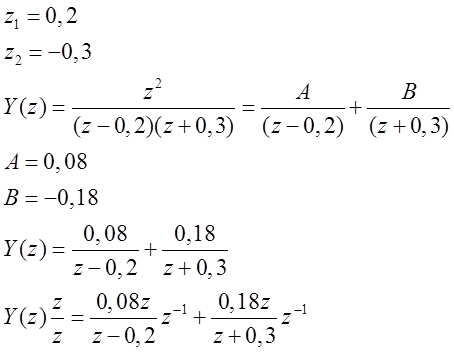
Т.к. 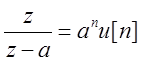 и по свойству запаздывания Z-преобразования получаем
и по свойству запаздывания Z-преобразования получаем
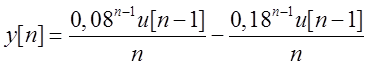
Проверка:
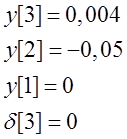
![]()
6. ДВПФ и его связь с Z-преобразованием
Прямое ДВПФ имеет вид 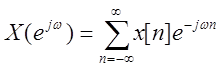 , где
, где ![]() -
непрерывная функция от ω, а x[n] – дискретный по времени сигнал. По
сути это выражение представляет собой ряд Фурье по переменной ω. Коэффициенты
ряда Фурье имеют вид
-
непрерывная функция от ω, а x[n] – дискретный по времени сигнал. По
сути это выражение представляет собой ряд Фурье по переменной ω. Коэффициенты
ряда Фурье имеют вид 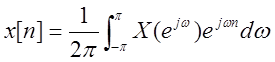 . Это выражение для
коэффициентов ряда представляет собой выражение обратного ДВПФ.
. Это выражение для
коэффициентов ряда представляет собой выражение обратного ДВПФ.
ДВПФ – это частный случай Z – преобразования (если на единичной
окружности ![]() , то Z – преобразование представляет собой ДВПФ).
, то Z – преобразование представляет собой ДВПФ).
Аналитически вычислим ДВПФ сигнала
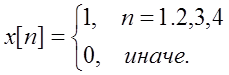
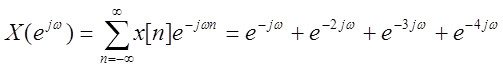 .
.
Аналитически вычислим z-преобразование сигнала
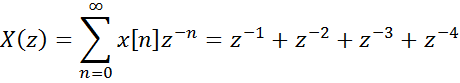
7. Вычисление ДВПФ с помощью файл-функции
function [X,w] = DTFT(x,M)
% Функция вычисляет значения DTFT от вектора x.
% Обращение
% [X,w] = DTFT(x,0)
% здесь X - вектор значений DTFT,
% w - вектор угловых частот.
% Если желательно вычислить DTFT с M значениями частоты,
% используется обращение
% [X,w] = DTFT(x,M)
%
% Этот вариант используется, когда размер вектора x
% меньше размера вектора частот w,
% при этом x дополняется нулевыми значениями
N = max(M,length(x));
% Приведение FFT к размеру 2^m
N = 2^(ceil(log(N)/log(2)))
% Вычисление fft
X = fft(x,N);
% Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi)
% Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
Найдем с помощью этой файл-функции ДВПФ сигналов
а) x[n] = e -0,5n,
б) 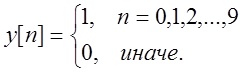
в) 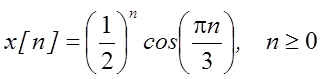
для значения M = 64.
а) x[n] = e -0,5n
>> n=0:1:5;
>> x=exp(-0.5*n);
>> t1=0:1:5;
>> stem(t1,x);
>> [X,w]=DTFT(x,64);
>> t=-31:1:32;
>> stem(t,abs(X))
>> figure(2)
>> stem(t,angle(X))
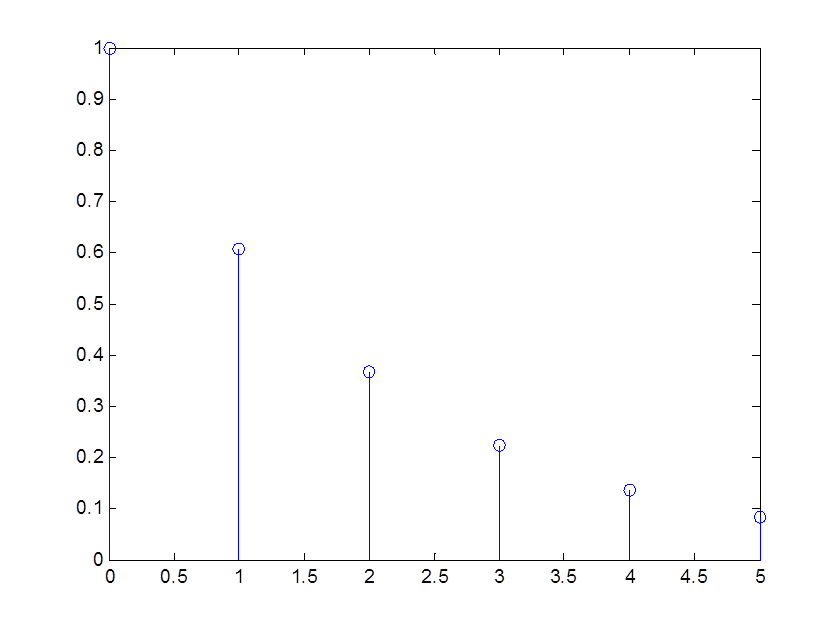
Рис. 1. График сигнала x[n] = e -0,5n
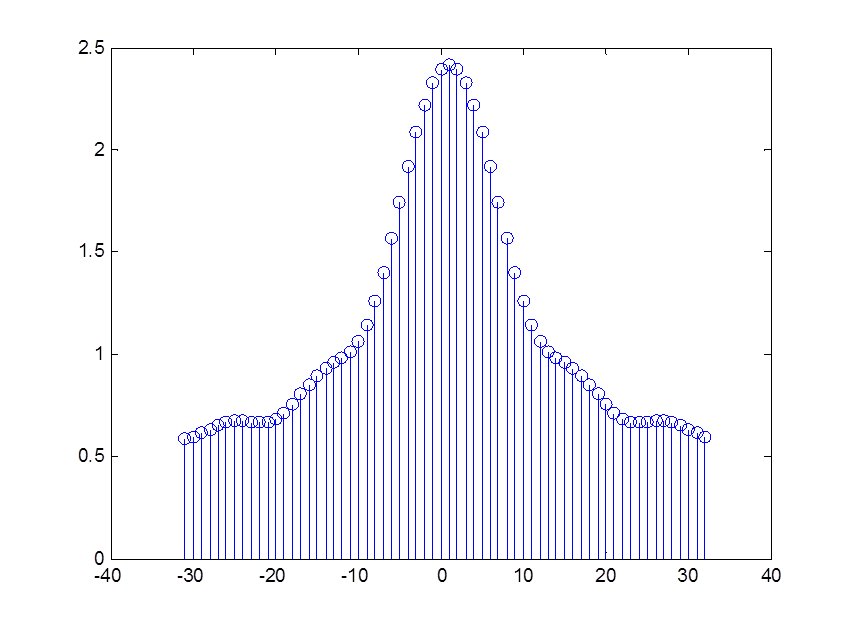
Рис. 2. Амплитудный спектр сигнала x[n] = e -0,5n
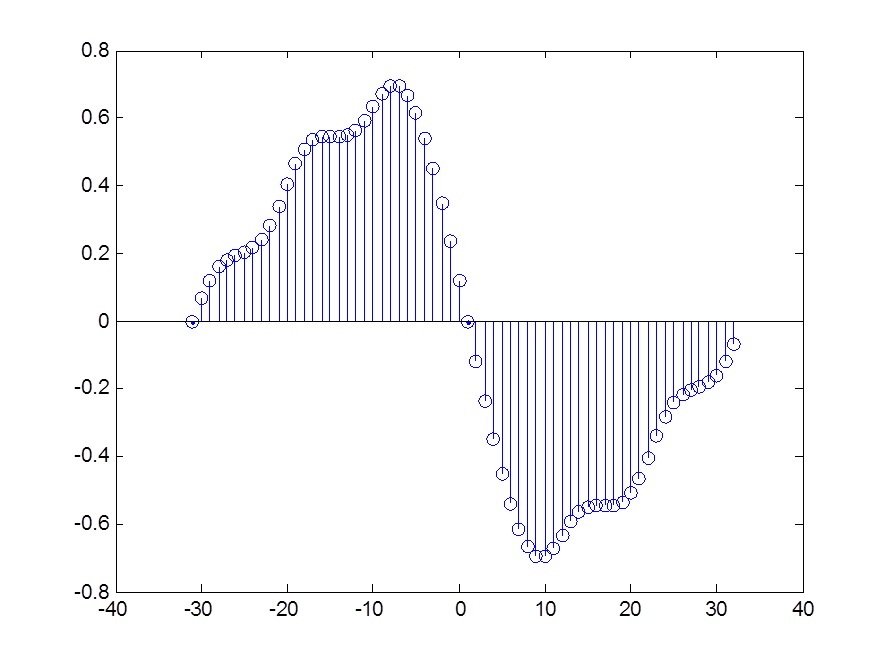
Рис. 3. Фазовый спектр сигнала x[n] = e -0,5n
б) 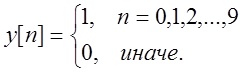
>> n=1:9;
>> x(n)=1;
>> t1=1:9;
>> stem(t1,x(n));
>> [X,w]=DTFT(x,64);
>> figure(1);
>> subplot(2,1,1)
>> stem(t,abs(X))
>> subplot(2,1,2)
>> stem(t,angle(X))
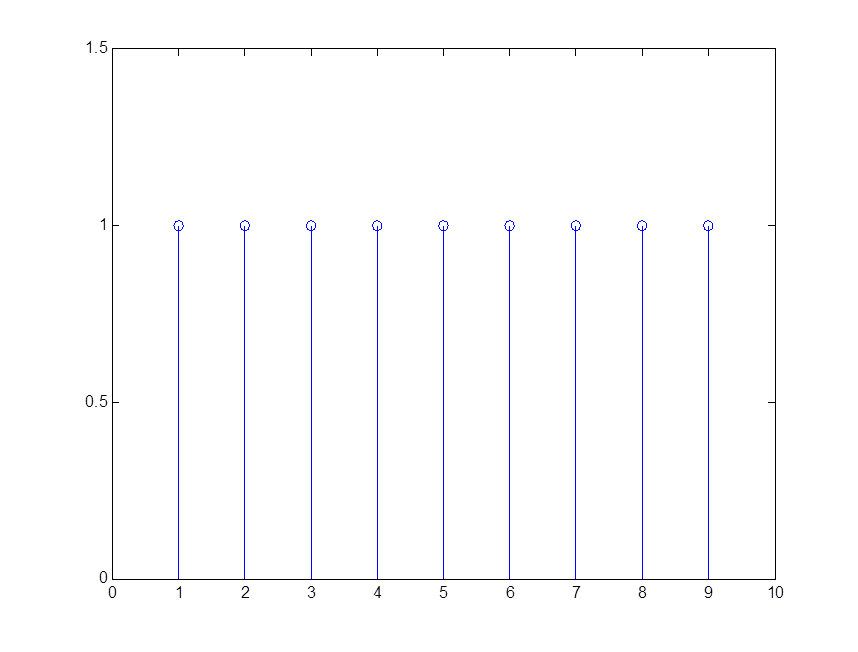
Рис. 4 График сигнала 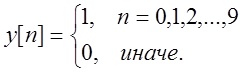
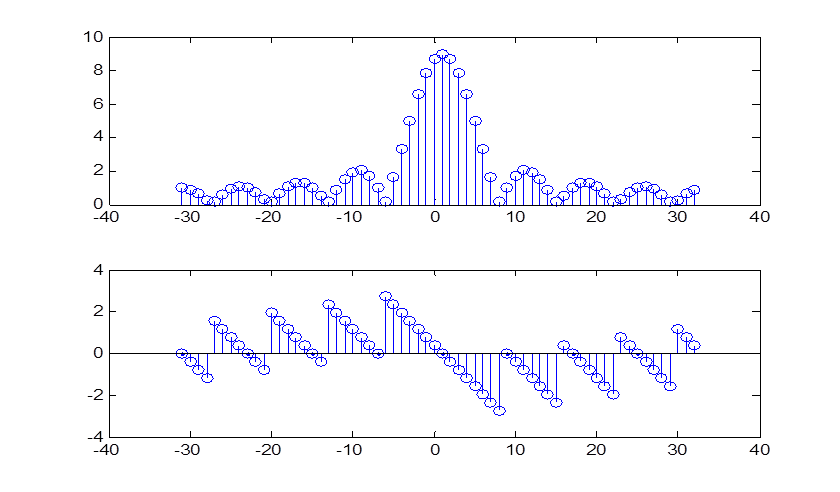
Рис. 5 Амплитудный и фазовый спектры
сигнала 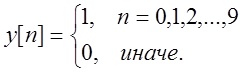
в) 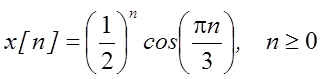
>> n=0:1:10;
>> x=(1/2).^n.*cos((pi/3).*n);
>> t1=0:1:10;
>> stem(t1,x);
>> [X,W]=DTFT(x,64);
>> subplot(2,1,1);
>> stem(t,abs(X));
>> subplot(2,1,2);
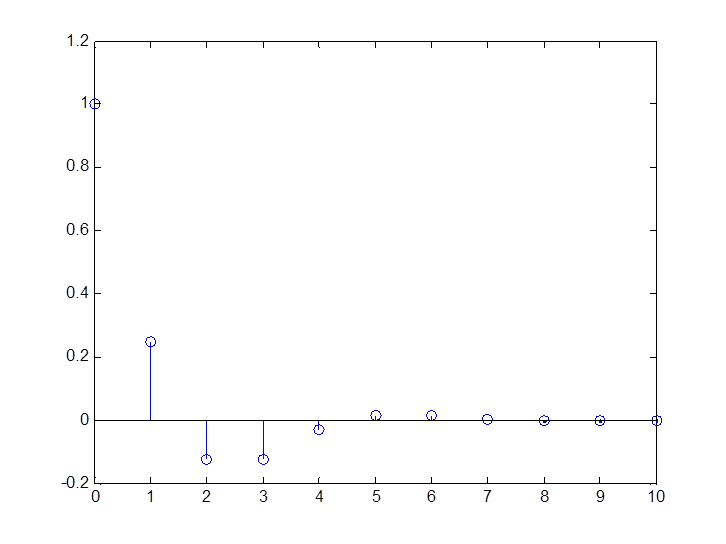 |
Рис. 6. График
сигнала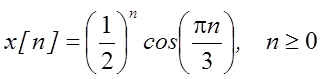
Рис. 7
Амплитудный и фазовый спектры сигнала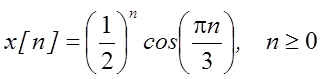
8. Свойства ДВПФ.
Для начала зададим и построим исходные сигналы и графики ДВПФ исходных сигналов:
N = 128; % Длина сигналов
k = 0:N-1;
gamma = -0.1;
g = exp(gamma*k);
% g - экспоненциальная функция
h = sin(2*pi*k/(N/4));
figure(1)
subplot(211),stem(k,g)
legend('exp(gamma*k)')
subplot(212),stem(k,h)
legend('sin(2*pi*k/(N/4))')
% h - синусоидальная последовательность с периодом = N/4
% вычисление ДВПФ
[G,w] = DTFT(g,512);
[H,w] = DTFT(h,512);
figure(2)
subplot(211), plot(w,abs(G))
subplot(212), plot(w,abs(H))
legend('w=2*pi/32=0,2')
Рис. 8. Графики исходных сигналов
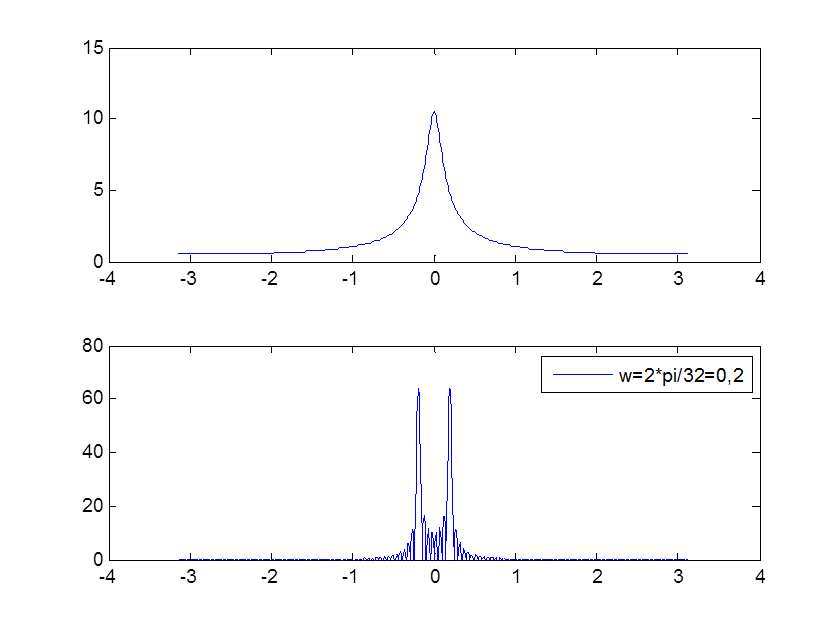
Рис. 9 Графики ДВПФ исходных сигналов
· Свойство линейности
% Свойство линейности
alpha = 0.5;
beta = 0.25;
y = alpha*g+beta*h;
[Y,w] = DTFT(y,512);
% Графики Y и alpha*G+beta*H для проверки их равенства
figure(3), subplot(211),plot(w,abs(Y))
subplot(212), plot(w,abs(alpha*G+beta*H))
%input(' Для продолжения нажмите любую клавишу')
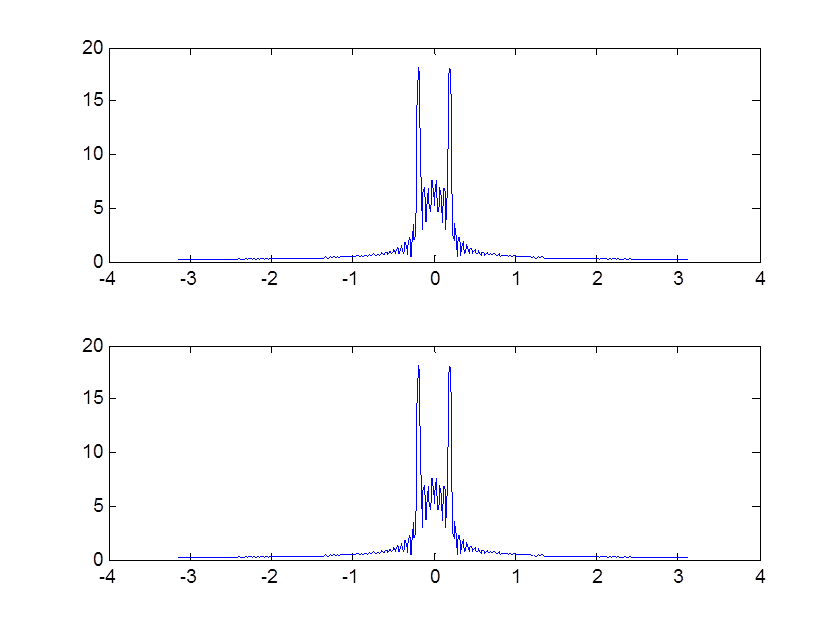
Рис. 10. Графики ДВПФ от суммы двух сигналов и суммы ДВПФ сигналов
Так как графики одинаковые, то это доказывает свойство линейности.
· Свойство временного сдвига
% Свойство временного сдвига
n0 = 12;
% y2 - последовательность y, сдвинутая на 12 отсчетов
y2 = [zeros([1,n0]) g];
[Y2,w] = DTFT(y2,512);
G0 = exp(-j*w*n0).*G;
% Графики амплитудных спектров
figure(4), subplot(211), plot(w,abs(G0))
subplot(212), plot(w,abs(Y2));
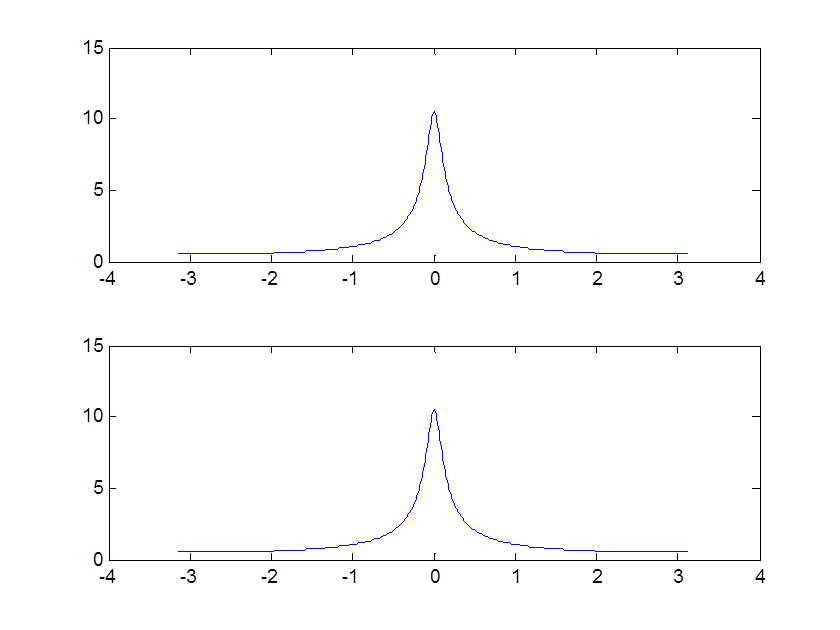
Рис. 11 иллюстрация свойства временного сдвига
Данные графики показывают, что временному сдвигу соответствует умножение ДВПФ на экспоненту в степени -jwn0, где n0 – временной сдвиг.
· Свойство изменения масштаба
% Свойство изменения масштаба
a=0.1; % Коэффициент изменения масштаба
g1= exp(gamma*k*a);
figure(4),plot(k,g,k,g1) % Графики во временной области
legend('g','g1')
[G,w] = DTFT(g,512);
G1 = DTFT(g1,512);
% Графики спектров
figure(5), subplot(211), plot(w,abs(G))
subplot(212), plot(w,abs(G1))
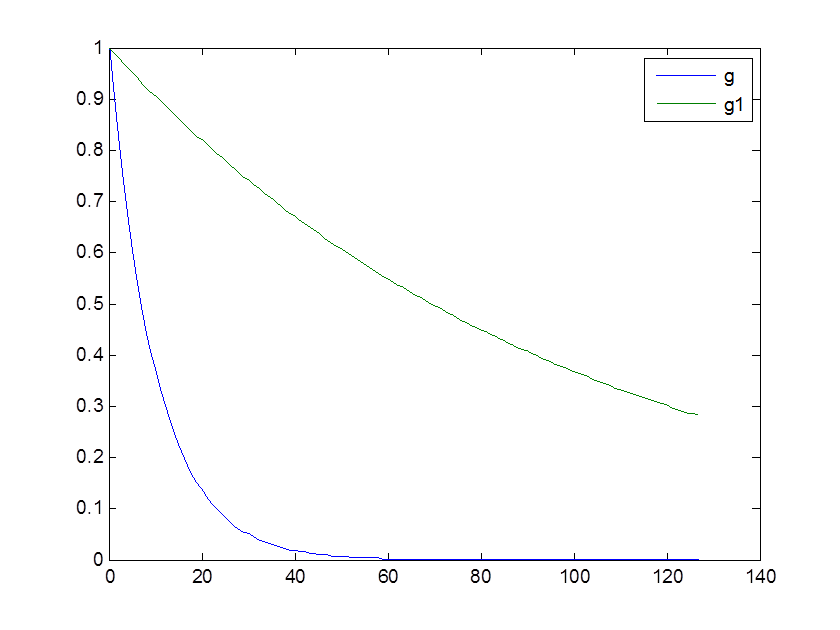
Рис. 12. Графики исходной экспоненты и масштабированной с коэффициентом 0.1
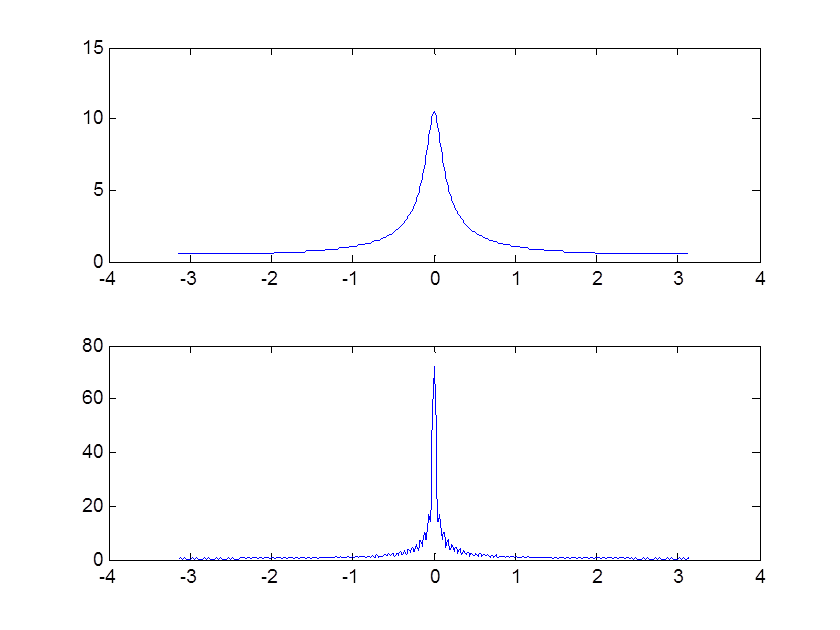
Рис. 13. ДВПФ обоих экспонент
· Свойство свертки
% Свойство свертки
y5 = conv(g,h);
[Y5,w] = DTFT(y5,512);
figure(6), subplot(211), plot(w,abs(Y5))
subplot(212), plot(w,abs(G.*H))
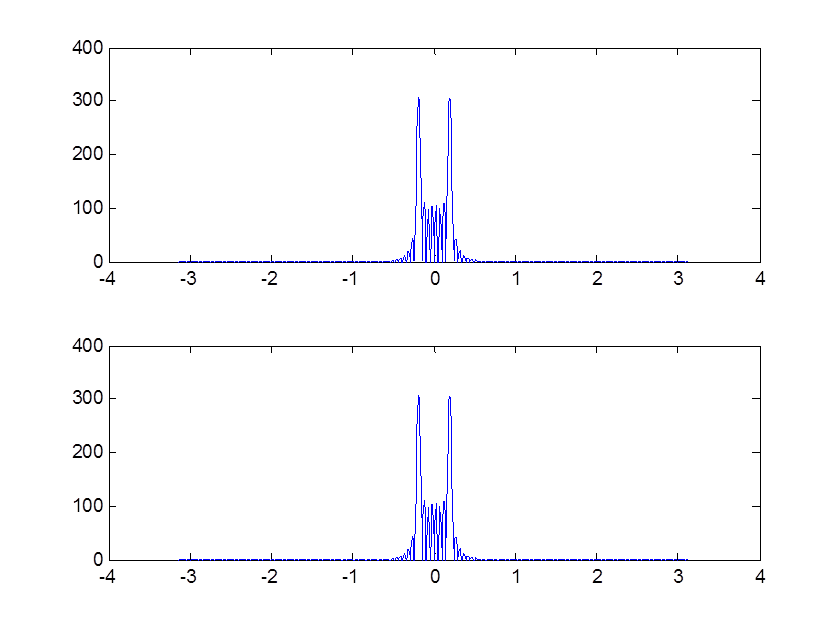
Рис. 14. Иллюстрация свойства свертки
Как видно из графиков свертке во временной области соответствует перемножение ДВПФ сигналов, участвующих в свертке.
· Теорема Парсеваля
% Теорема Парсеваля
val1 = sum(g.*g);
val2 = sum(G.*conj(G))/512;
% Сравнение val1 с val2
disp('Разность val1-val2 = ')
disp(val1-val2)
Разность val1-val2 = 0
Так как разность нулевая, это означает что энергию сигнала можно вычислить перемножением ДВПФ сигнала на его комплексно-сопряженное.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.