Информатика и выч. техника \ Теория и обработка сигналов

Изучение методов анализа линейных дискретных стационарных систем. Вариант 7, страница 2

Полюса и нули лежат внутри единичной окружности - система устойчива, что соответствует виду импульсной характеристики.

4.  Расчёт частотной характеристики с помощью функции freqz, построение графиков АЧХ и ФЧХ. Определение частоты среза.

num = [2 -2];

den = [1 -0.98];

freqz(num, den, 1000, 10^5)

[H f] = freqz(num, den, 1000, 10^5);

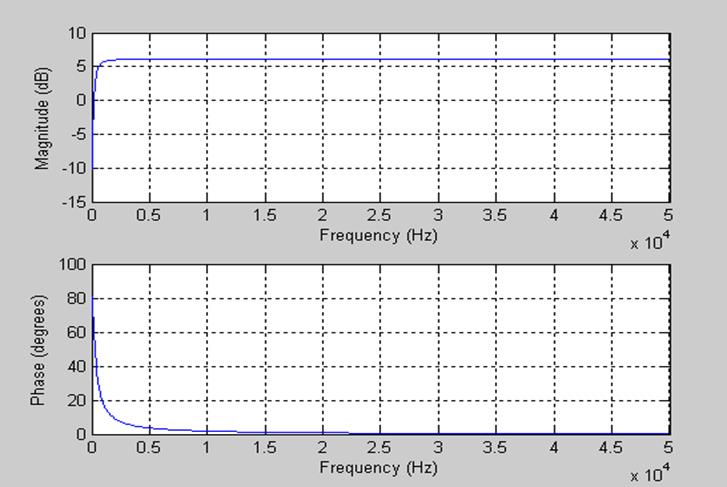
Рис.6 Графики АЧХ и ФЧХ .ДС.

min = 5;

for i = 1:1:1000

    if abs(abs(H(i))-max(abs(H))/sqrt(2))<min

        min = abs(abs( H(i))-(max( abs(H))/sqrt(2)))

        count = i

    end

end

disp('-------------------------------------------');

disp('---------------частота среза---------------');

f(count)

angle(H(count))*57.296

min

disp('-------------------------------------------');

%////////////////////////////////////////////////////////////////////

----------------------------------------------

---------------частота среза---------------

ans = 300

ans = 46.9829

min = 0.0503

Убеждаемся, что система является ФВЧ.

5.  Исследование свойства фильтрации системы с использованием  функций filter() и dlsim().

%Демонстрация фильтрующего свойства системы

Fd=10^5;     %Hz

f_out = 50;  %Hz

f_in = 1000; %Hz

n=0:2000;

x=cos(2*pi*f_in*n/Fd);  %первый сигнал - в полосе пропускания

subplot(4,1,1)

plot(n./Fd,x),grid;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

xlabel('сек');

y=cos(2*pi*f_out*n/Fd); %второй сигнал - в полосе задержания

subplot(4,1,2)

plot(n./Fd,y),grid;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

xlabel('сек');

Rez=x+y;

subplot(4,1,3)

plot(n./Fd,Rez),grid;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

xlabel('сек');

num = [2  -2];

den = [1 -0.98];

F=filter(num,den,Rez);

subplot(4,1,4)

plot(n./Fd,F),grid;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

xlabel('сек');

%////////////////////////////////////////////////////////////////////

figure(2);

r = dlsim(num,den,Rez);grid;

hold on

plot(n./Fd,Rez,'r');

plot(n./Fd,r);

hold off;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

title('Демонстрация фильтрующих свойств (с исп-ием функции dlsim)')

legend('До фильтра','После фильтра')

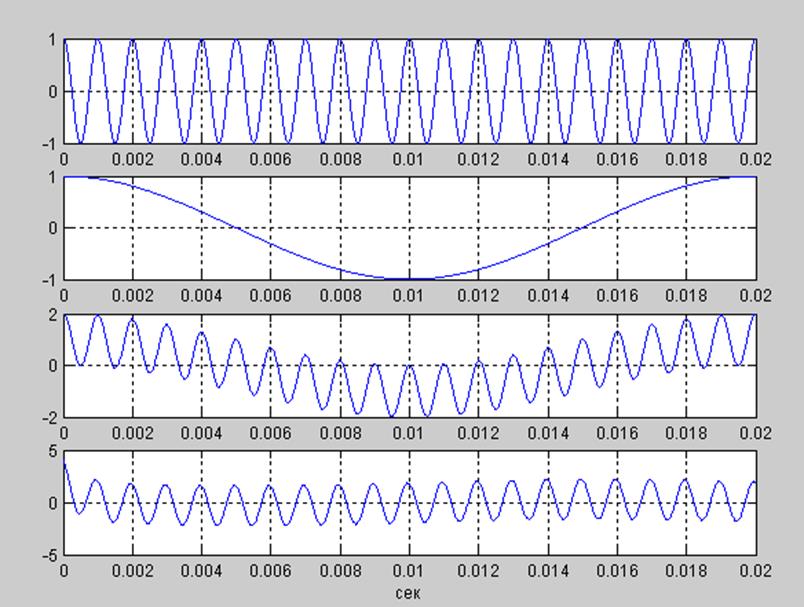
Рис.7.1 Демонстрация фильтрующего свойства системы (фильтра)

(с использованием функции filter() )

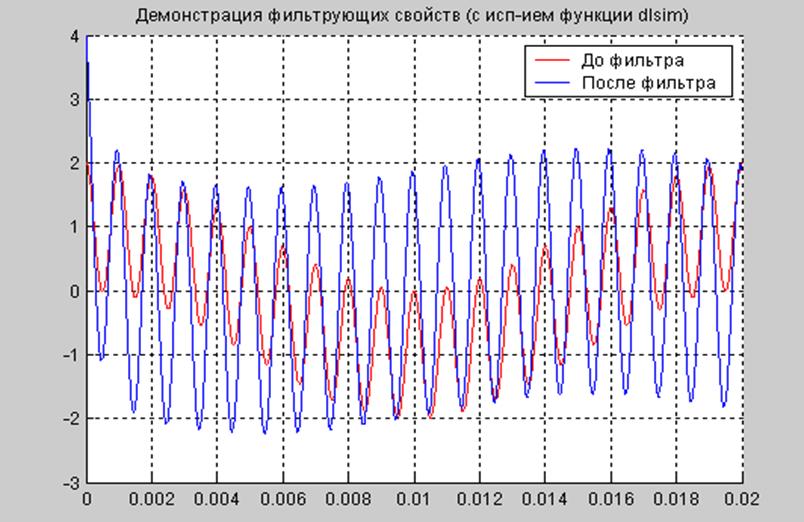
Рис.7.2 Демонстрация фильтрующего свойства системы (фильтра)

(с использованием функции dlsim() )


6.  Исследование влияния расположения нулей и полюсов на частотную характеристику системы. 

Исходные значения  нулей и полюсов.

nulls =1

polus = 0.9800

Общий вид передаточной функции для дискретной системы

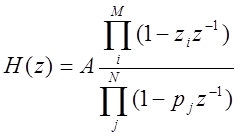
А, следовательно, выражение для АЧХ

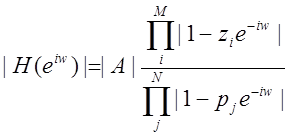
Выражение для АЧХ при одном нуле и одном полюсе.

(9)
 

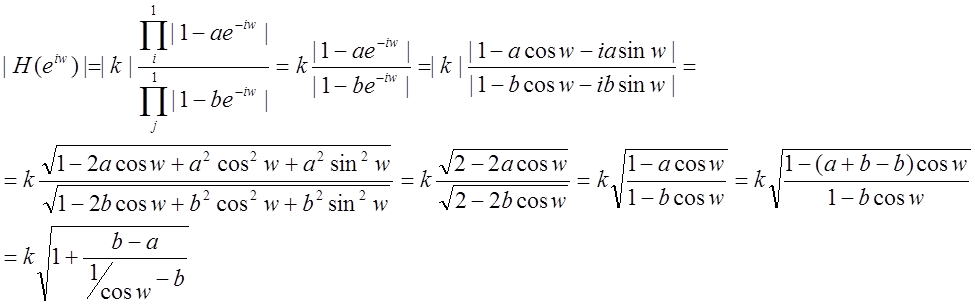
Т.о. АЧХ системы можно построить, зная расположение её нулей и полюсов.

При уменьшении действительного значения полюса частотные характеристики более пологие.

Значение полюса нельзя увеличить таким образом, чтобы оно стало более единицы, поскольку дискретная система станет неустойчивой.

7.  Определение импульсной характеристики системы с использованием функции impz(),а также  построение её графика.

%Вектор коэффициентов числителя:

num=[2 -2];

%Вектор коэффициентов знаменателя:

den=[1 -0.98];

figure(1);

impz(num,den),grid;

set(gca,'FontName','Arial Unicode MS','FontSize',9);

figure(2);

dimpulse(num,den,100);

%/////////////////////////////////////////////////////////////////////

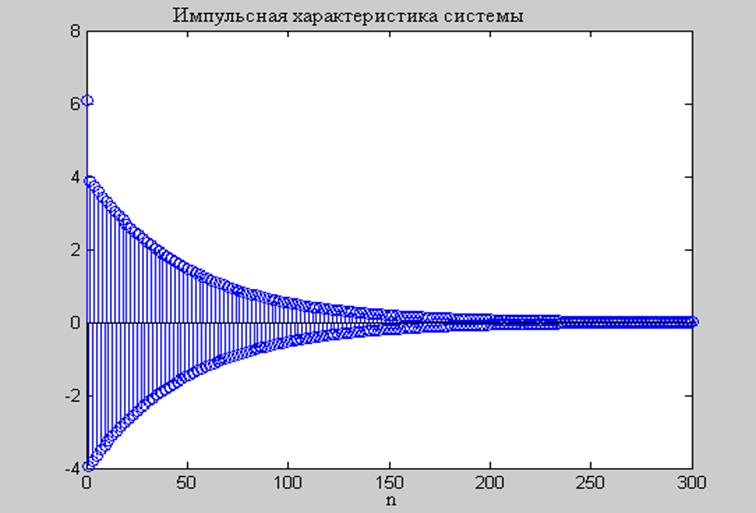
Рис. 8. График импульсной характеристики, построенной с использованием функции impz()

График импульсной характеристики на рис.8 совпадает с графиком аналитически определенной импульсной характеристики (рис. 4).

8.  Построение графика переходной характеристики фильтра  с помощью функции dstep().

Переходная характеристика – это реакция системы на входной сигнал в виде единичной последовательности при нулевых начальных условиях. Её можно определить через импульсную характеристику:

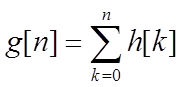
Это можно подтвердить, проанализировав импульсную и переходную характеристики нашей системы (рис. 4, 8, и рис. 9)

C помощью следующей последовательности команд построим график переходной характеристики системы, воспользовавшись функцией dstep().

%Вектор коэффициентов числителя:

num=[2 -2];

%Вектор коэффициентов знаменателя:

den=[1 -0.98];

figure(1);

dstep(num,den);grid;

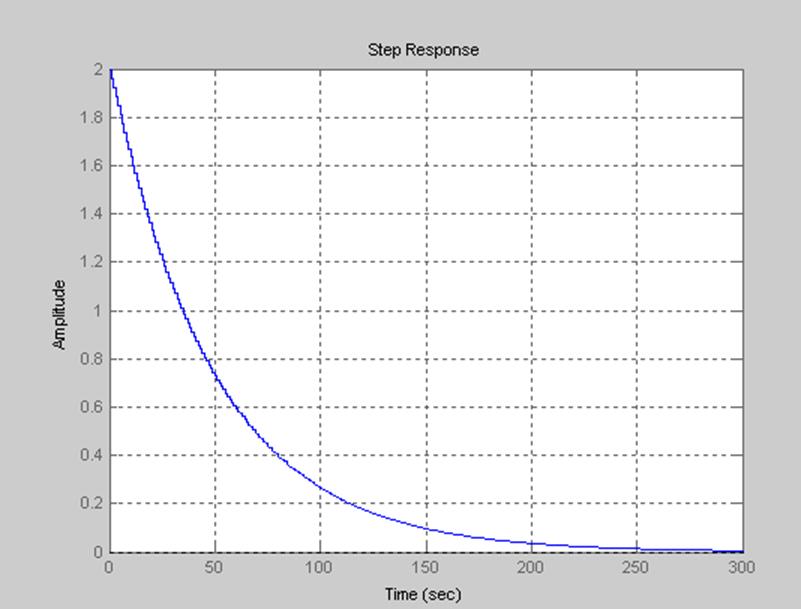
Рис.9График переходной характеристики системы, построенной с использованием функции dstep()

Выводы:

1.  Одним из способов получения дискретных фильтров является преобразование аналогового фильтра в дискретный, удовлетворяющий определенным требованиям.

Дискретные линейные стационарные системы описываются линейными разностными уравнениями с постоянными коэффициентами.

Разностное уравнение, описывающее дискретную систему можно получить из дифференциального уравнения, задающего аналоговую систему, с помощью процедуры дискретизации (замена производных в дифференциальном уравнении конечными разностями).

Такую процедуру мы провели в пункте 1 и проанализировали ее результаты:  

АЧХ дискретной системы сходится с АЧХ аналоговой системы, которую мы дискретизировали (см. рис. 3)

2.  Также в пункте 1 мы получили передаточную функцию ДС (характеристика систем в области переменной z), использовав обратное Z-преобразование для линейного разностного уравнения системы.

3.  В пункте 2 лабораторной работы мы разложили передаточную функцию на простые дроби при помощи функции residues(), нашли импульсную характеристику ДС как обратное Z-преобразование передаточной функции системы, построили её график (рис.4) и убедились, что система устойчива.

4.  В пункте 3 мы нашли полюса и нули дискретной системы (в нашем случае – один полюс и один нуль), построив диаграмму (рис.5), получили, что расположение нулей и полюсов соответствует импульсной характеристике (рис.4)

5.  В пункте 4, с использованием функции freqz(), мы нашли АЧХ и ФЧХ исследуемой системы, а также частоту среза.

6.  Исследование свойства фильтрации системы с использованием функций filter() и dlsim() были проведены в пункте 5.

7.  По расположению нулей и полюсов системы на z-плоскости можно судить об её устойчивости, а оперируя значениями нулей и полюсов можно изменять характеристики систем (пункт 6).

8.  График импульсной характеристики, полученной с помощью функции impz() (рис.8) в пункте 7 совпадает с графиком аналитически определённой импульсной характеристики (рис.4) в пункте 2.

9.  Воспользовавшись функцией dstep(), построили график переходной характеристики системы (пункт 8).

Общий вывод:    в ходе выполненной лабораторной работы мы преобразовали аналоговый фильтр    в дискретный и провели анализ его характеристик и свойств при помощи средств Matlab.

Скачать файл