x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
t2=cputime-t1; % Конец времени вычисления
% Построение графиков во временной и частотной области
figure;
subplot(211), plot(t,x)
subplot(212), plot(t,abs(y))
Результат выполнения:
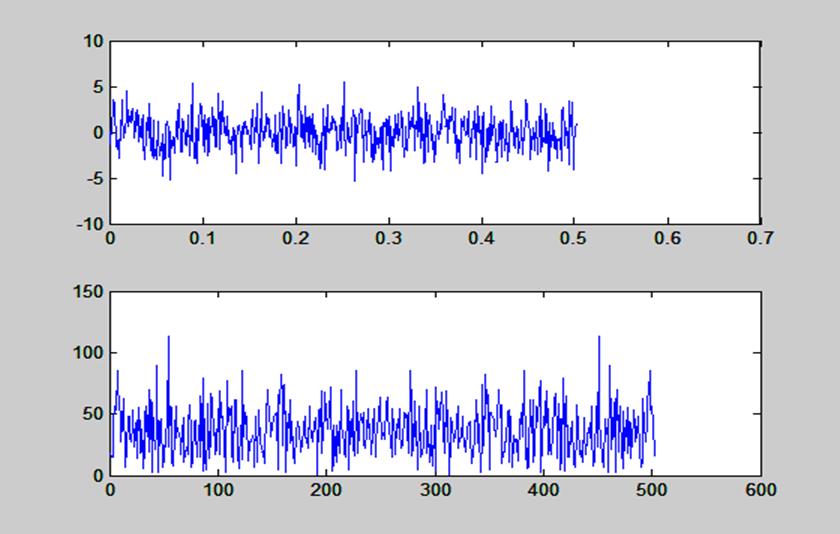
Рис. 7. Графики случайной последовательности длиной 503 точки и ее ДПФ, вычисленного с
помощью функции dftsum()
Время вычисления ДПФ случайной последовательности длинной 503 точки с помощью функции dftsum(x):
t2 = 0.2710 с
2. Вычислить ДПФ случайной последовательности длиной 503 точки с
помощью встроенной в Matlab функции fft(). Определить (функция
cputime) время вычисления ДПФ и сопоставить его с временем
вычисления функции
dftsum().
Представить в отчете
в краткой форме описание алгоритма БПФ с
прореживанием по времени.
М-файл для вычисления ДПФ случайной последовательности с помощью встроенной функции fft(x):
t=0:0.001:0.502;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=fft(x,503); % Вычисление ДПФ
t2=cputime-t1;% Конец времени вычисления
% Построение графиков во временной и частотной области
figure;
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
Результат выполнения:
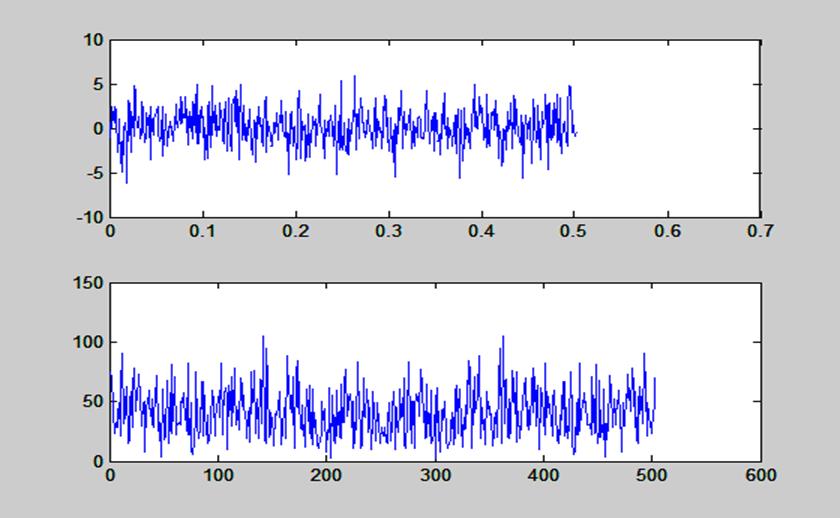
Рис. 8. Графики случайной последовательности длиной 503 точки и ее ДПФ, вычисленного с
помощью функции fft()
Время вычисления ДПФ случайной последовательности длинной 503 точки с помощью функции fft(x):
t2 = 0.0200
По полученным результатам видно, что для данной последовательности время вычисления ДПФ с помощью функции fft(x) на порядок меньше, чем при помощи функции dftsum(x).
Это объясняется тем, что в функции fft() используется алгоритм быстрого преобразования Фурье.
Алгоритмы БПФ основываются на представлении величины N (длины преобразования) в виде ряда сомножителей, больших единицы:
N=r1*r2*…*rq.
При этом последовательность S[n]
может быть представлена итеративно путем вычисления суммы q
слагаемых: N/r1 преобразований Фурье , каждое из которых требует ![]() операций, N/r2
преобразований Фурье с количеством операций
операций, N/r2
преобразований Фурье с количеством операций ![]() и
т д., наконец, N/rq преобразований Фурье с количеством операций
и
т д., наконец, N/rq преобразований Фурье с количеством операций ![]() . Таким образом, общее число
операций над действительными числами составляет
. Таким образом, общее число
операций над действительными числами составляет 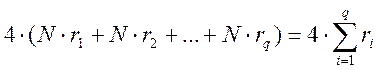 .
Время вычисления алгоритмов БПФ пропорционально
.
Время вычисления алгоритмов БПФ пропорционально ![]() .
.
3. Определить ближайшее сверху к значению 503 число, являющееся
степенью 2. Найти время вычисления ДПФ для последовательности
такой длины с помощью функций dftsum() и fft(). При вычислении с
помощью fft() организовать цикл из 1000 вычислений и разделить
общее время вычисления цикла на 1000.
Объяснить различие времени вычисления для рассматриваемого
случая по сравнению с предшествующим пунктом работы.
Ближайшее сверху к значению
503 число, являющееся степенью 2 – 512.
М-файл для вычисления ДПФ последовательности длиной 512 точек с помощью функции dftsum():
t=0:0.001:0.511;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=dftsum(x); % Вычисление ДПФ
t2=cputime-t1;% Конец времени вычисления
% Построение графиков во временной и частотной области
figure;
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
Результат выполнения:
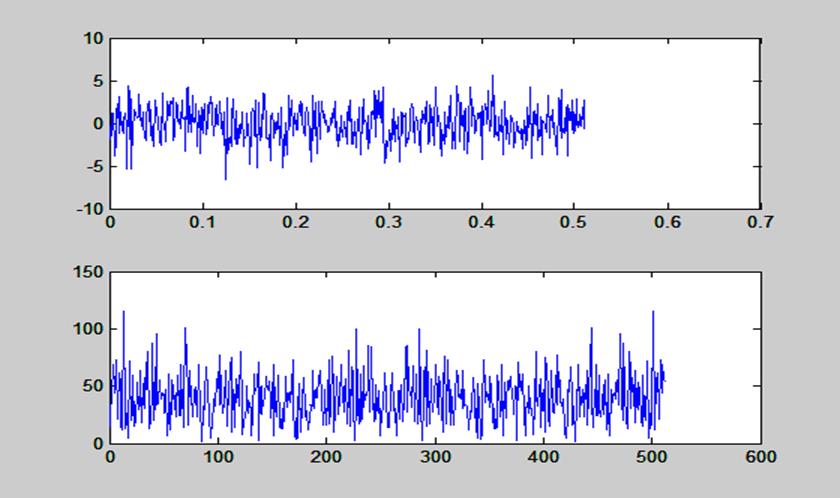
Рис. 9. Графики случайной последовательности длиной 512 точки и ее ДПФ, вычисленного с
помощью функции dftsum()
Время выполнения: t2 = 0.2610
М-файл для вычисления ДПФ последовательности длиной 512 точек с помощью функции fft():
t=0:0.001:0.511;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=fft(x,1000); % Вычисление ДПФ
t2=(cputime-t1)/1000; % Конец времени вычисления
% Построение графиков во временной и частотной области
figure;
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
Результат выполнения:
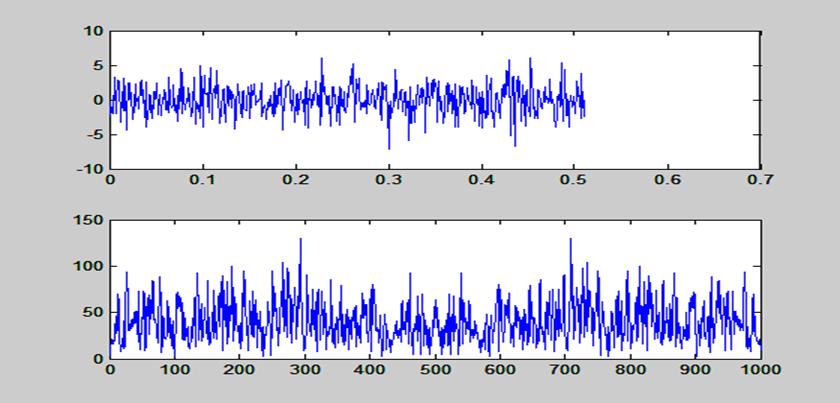
Рис. 10. Графики случайной последовательности длиной 512 точки и ее ДПФ, вычисленного с
помощью функции fft()
Время выполнения: t2 = 4.0000e-005.
Время выполнения функции dftsum() для последовательности из 503 и 512 точек примерно равны.
Время выполнения функции fft() для последовательности из 512 точек на три порядка меньше, чем для последовательности из 503 точек. Это объясняется тем, что время выполнения алгоритма быстрого дискретного преобразования Фурье минимально для последовательностей размера, являющегося степенью числа 2.
4. Предполагая, что время вычисления БПФ при основании 2
пропорционально ![]() (N –
длина последовательности), оценить
(N –
длина последовательности), оценить
время вычисления для последовательности длиной 4096. Константу
коэффициента пропорциональности найти из предыдущих
вычислений. Определить действительное время вычисления БПФ
длиной 4096, сопоставить с оценкой времени.
Найдем константу коэффициента:
![]()
![]()
Оценим время вычисления БПФ для последовательности из 4096 точек:
![]()
t=0.00053
М-файл для вычисления ДПФ последовательности длиной 4096 точек с помощью функции fft():
t=0:0.0001:0.4095;
% Формирование случайной последовательности
x=2*randn(size(t));
t1=cputime; % Начало времени вычисления ДПФ
y=fft(x); % Вычисление ДПФ
t2=cputime-t1 % Конец времени вычисления
% Построение графиков во временной и частотной области
figure;
subplot(211), plot(t,x)
subplot(212), plot(abs(y))
Результат выполнения:
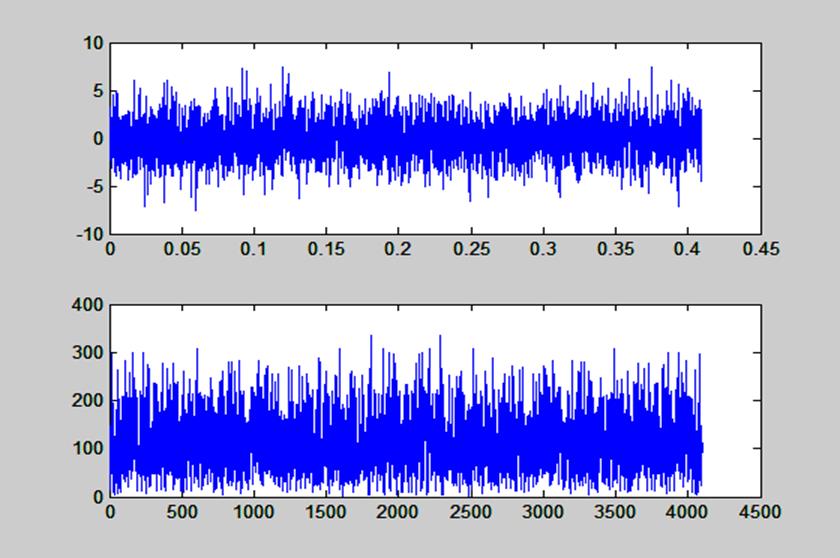
Рис. 11. Графики случайной последовательности длиной 4096 точки и ее ДПФ, вычисленного с
помощью функции fft()
Время вычисления: t2=0.
![]()
5.
Создать две
последовательности длиной по 16 точек каждая
а) 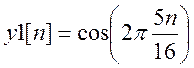 , б)
, б) 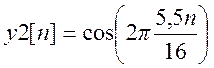 .
.
Вычислить ДПФ для обеих последовательностей и построить
графики амплитудного спектра с использованием функции stem().
Дополнить каждую из последовательностей 48 точками из нулей до
длины 64 точки и построить графики амплитудного спектра для
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.