обеих
последовательностей. Сравнить с предыдущими графиками.
Создать последовательности косинусоидальных гармоник длиной
N = 64. Построить графики амплитудных спектров для этого случая
и сравнить с предшествующими результатами.
М-файл для создания косинусоидальных последовательностей и вычисления их ДПФ:
n=0:15;
%создание последовательностей
y1=cos(2*pi*5.*n/16);
y2=cos(2*pi*5.5.*n/16);
%вычисление ДПФ
x1=dftsum(y1);
x2=dftsum(y2);
figure;
subplot(211), plot(n,abs(y1)),
title('y1');
subplot(212), stem(n,x1),
figure;
subplot(211), plot(n,y2),
title('y2');
subplot(212), stem(n,x1)
Результат выполнения:
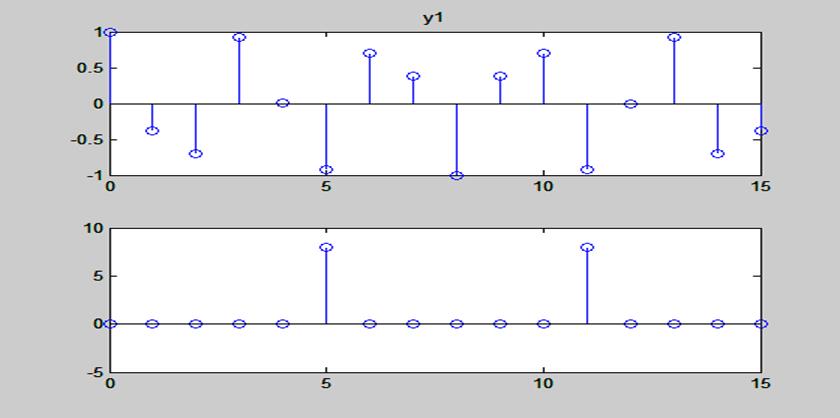
Рис. 12. Графики косинусоидальной последовательности y1=cos(2*pi*5*n/16);
длиной 16 точек и ее ДПФ
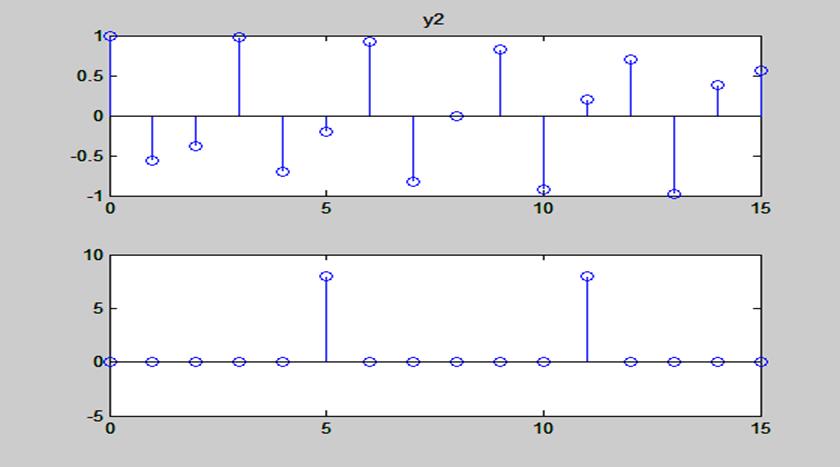
Рис. 13. Графики косинусоидальной последовательности y2=cos(2*pi*5.5*n/16);
длиной 16 точек и ее ДПФ
Графики амплитудных спектров двух косинусоидальных последовательностей совпадают.
М-файл для дополнения косинусоидальных последовательностей до 64 точек нулями и вычисления их ДПФ:
n=0:15;
%определение последовательностей
y1=cos(2*pi*5.*n/16);
y2=cos(2*pi*5.5.*n/16);
%дополнение последовательностей нулями
y1z=[y1 zeros(1,48)];
y2z=[y2 zeros(1,48)];
%вычисление ДПФ последовательностей
x1=dftsum(y1z);
x2=dftsum(y2z);
nz=0:63;
figure;
subplot(211), stem(nz,y1z),
title('y1');
subplot(212), stem(nz,x1),
figure;
subplot(211), stem(nz,y2z),
title('y2');
subplot(212), stem(nz,x1),
Результат выполнения:
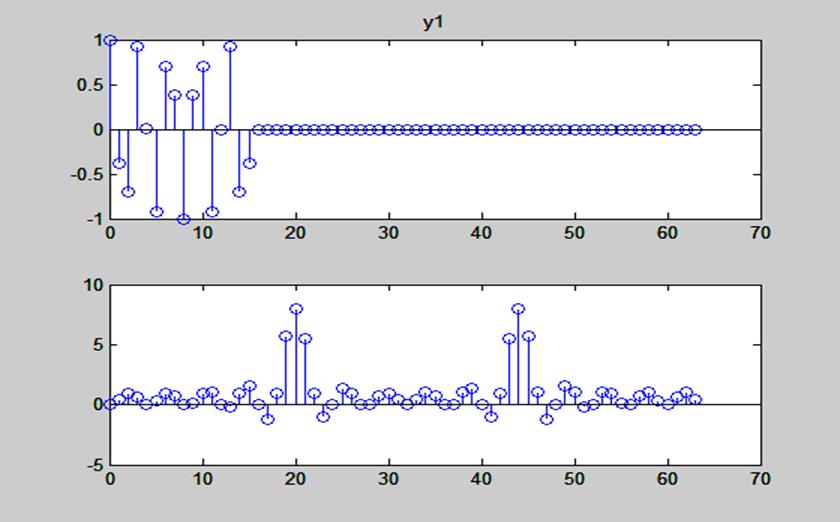
Рис. 14. Графики косинусоидальной последовательности y2=cos(2*pi*5*n/16)
дополненной нулями и ее ДПФ
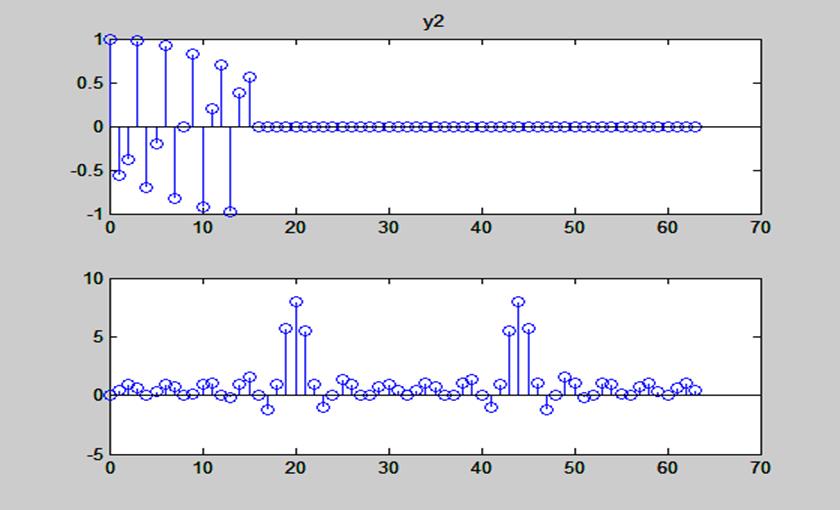
Рис. 15. Графики косинусоидальной последовательности y2=cos(2*pi*5.5*n/16);
дополненной нулями и ее ДПФ
Графики амплитудных спектров двух косинусоидальных последовательностей совпадают.
М-файл для создания косинусоидальных последовательностей длиной 64 точки и вычисления их ДПФ:
n=0:63;
%создание последовательностей
y1=cos(2*pi*5.*n/16);
y2=cos(2*pi*5.5.*n/16);
%вычисление ДПФ последовательностей
x1=dftsum(y1);
x2=dftsum(y2);
figure;
subplot(211), stem(n,y1),
title('y1');
subplot(212), stem(n,x1),
figure;
subplot(211), stem(n,y2),
title('y2');
subplot(212), stem(n,x1),
Результат выполнения:
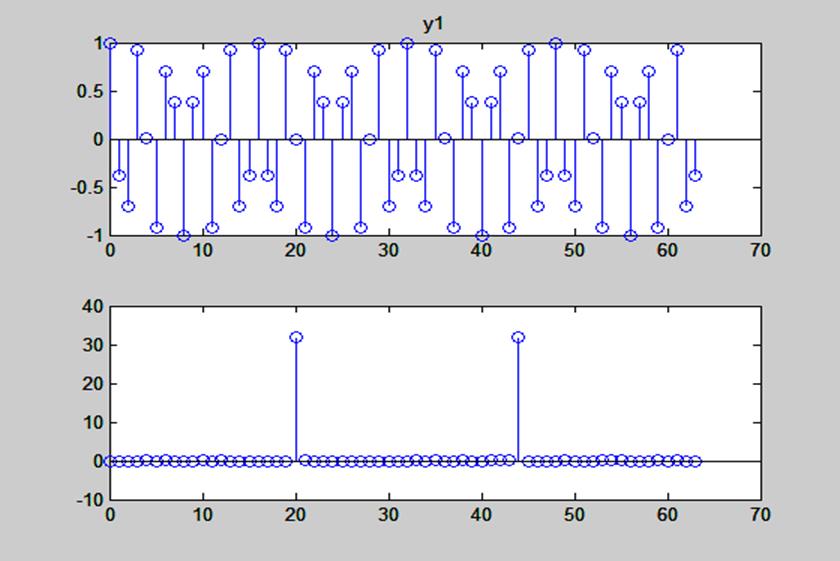
Рис. 16. Графики косинусоидальной последовательности y2=cos(2*pi*5*n/16);
длиной 64 точки и ее ДПФ
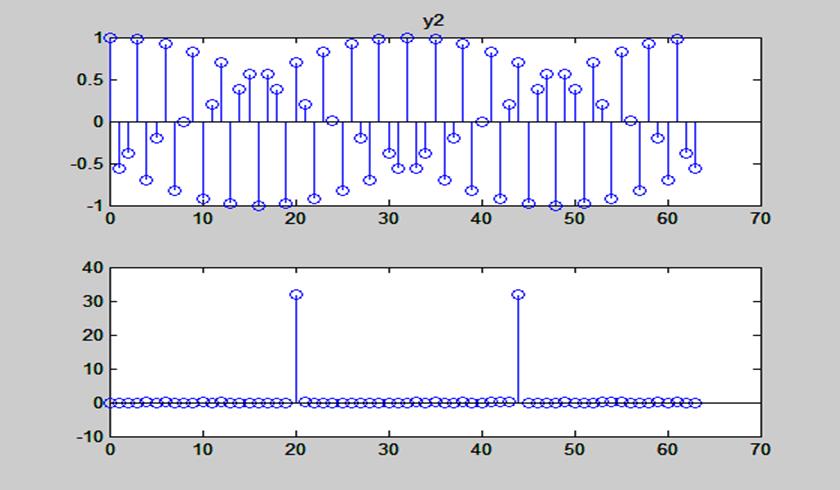
Рис. 17. Графики косинусоидальной последовательности y2=cos(2*pi*5.5*n/16);
длиной 64 точки и ее ДПФ
Графики амплитудных спектров двух косинусоидальных последовательностей совпадают.
6. Сгенерировать экспоненциальный дискретный сигнал
длительностью 100 отсчетов и прямоугольный сигнал из 40
отсчетов. Выполнить дискретную свертку этих сигналов (функция
conv) и представить её график. Далее выполнить свертку этих
сигналов с помощью БПФ (круговая свертка) и
сравните с результатами, полученными функцией conv().
М-файл для генерирования двух сигналов и выполнения их свертки:
%генерирование экспоненциального сигнала
n1=0:0.01:0.99;
y1=exp(n1);
%генерирование экспоненциального сигнала
n2=0:0.01:0.39;
for i=1:40
y2(i)=1;
end
%вычисление свертки сигналов
y=conv(y1,y2);
figure;
subplot(211), stem(n1,y1)
hold on
stem(n2,y2,'g');
subplot(212), stem(y);
Результат выполнения:
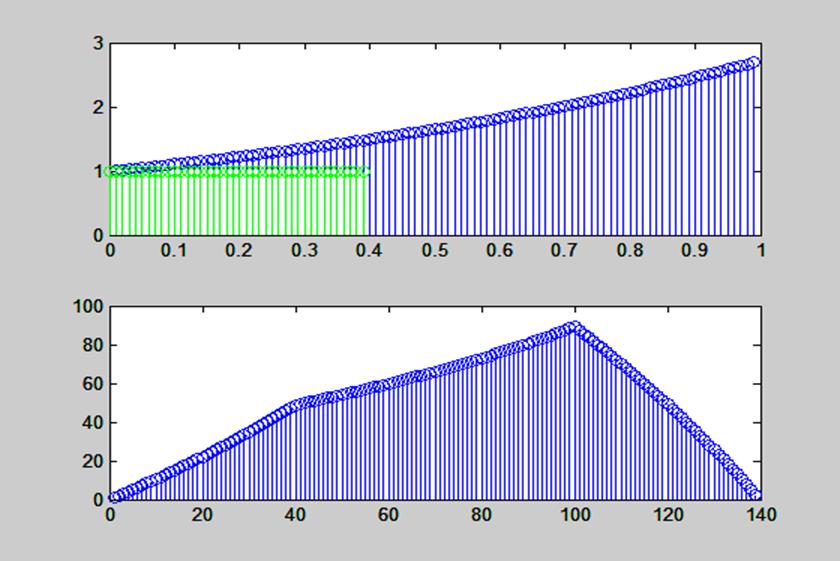
Рис. 18. Графики экспоненциального и прямоугольного сигналов и их свертка,
выполненная при помощи функции conv()
М-файл для выполнения круговой свертки сигналов:
%генерирование экспоненциального сигнала
n=0:0.01:0.99;
y1=exp(n);
%генерирование экспоненциального сигнала
n2=0:0.01:0.39;
for i=1:40
y2(i)=1;
end
%дополнение последовательностей нулями
y1z=[y1 zeros(1,156)];
y2z=[y2 zeros(1,216)];
%вычисление ДПФ последовательностей
y1f=fft(y1z);
y2f=fft(y2z);
yf=y1f.*y2f; %произведение ДПФ последовательностей
x=ifft(yf); %ОДПФ произведения
figure;
n1=0:0.01:2.55;
n2=0:0.01:2.55;
subplot(211),
stem(n1,y1z)
hold on
stem(n2,y2z,'g');
subplot(212), stem(abs(x));
title('Круговая свертка')
Результат выполнения:
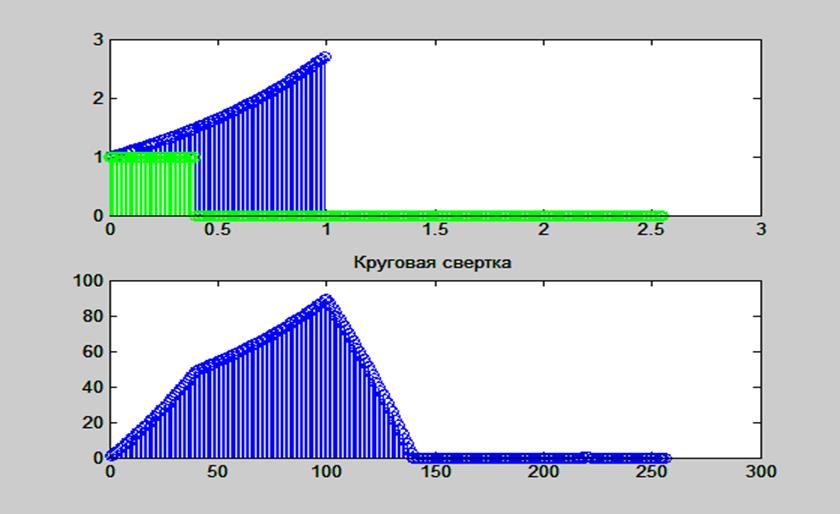
Рис. 19. Графики экспоненциального и прямоугольного сигналов, дополненных нулями и их
круговая свертка.
7. Выполнить пример использования преобразования Фурье для
выделения полезного сигнала из смеси с шумом. Для этого
сформировать сигнал, являющийся суммой двух синусоид
единичной амплитуды с частотами 50 и 100 Гц и случайного
аддитивного нормального шума с нулевым средним значением и
средним квадратическим отклонением, равным 2. Построить
график этого сигнала во временной области.
Вычислить спектральную плотность мощности (СПМ) сигнала.
Постройте график СПМ.
М-файл для построения сигнала и вычисления его спектральной плотности мощности:
t=0:0.001:0.6;
%формирование сигнала
x=sin(2*pi*50*t)+sin(2*pi*100*t);
y1=x+2*random('norm',0,2,size(t));
figure;
subplot(211), plot(y1(1:100)), grid
title('График зашумленного сигнала')
%вычисление спектральной плотности мощности сигнала
y=fft(y1,512);
pyy=y.*conj(y)/512;
f=1000*(0:255)/512;
subplot(212), plot(f, pyy(1:256)),grid
title('График спектра мощности')
Результат выполнения:
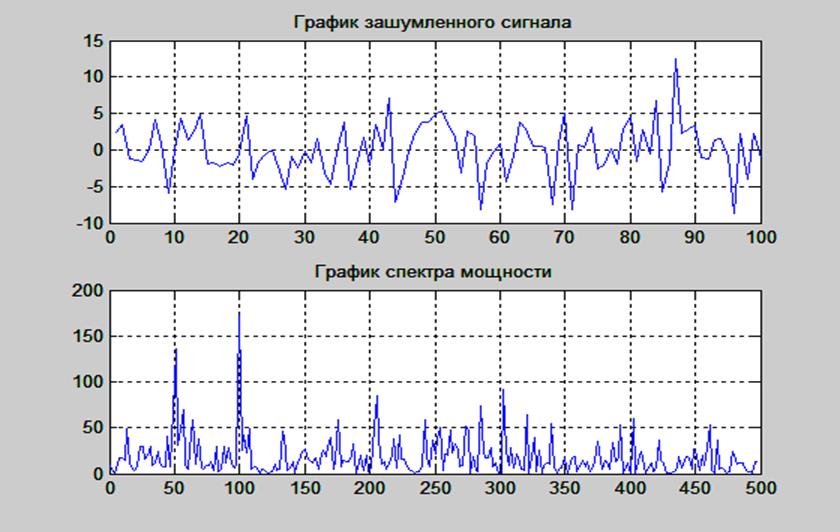
Рис. 20. Графики зашумленного сигнала и его спектра мощности
8. Вывод: в работе были найдены ДПФ и ОДПФ нескольких сигналов с помощью написанных нами функций dftsum() и idftsum() соответственно и построены графики амплитудных спектров для каждого случая. Было произведено вычисление ДПФ случайных последовательностей длиной 503 и 512 точек с помощью функции dftsum() и fft() и найдено время вычисления ДПФ для каждого случая. Кроме того, были найдены ДПФ и построены графики амплитудных спектров двух косинусоидальных последовательностей для разного числа точек и изучено использование преобразования Фурье для выделения полезного сигнала из смеси с шумом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.