Генерирование непрерывных и дискретных по времени сигналов, построение графиков сигналов в среде MATLAB, страница 2

Функция tripuls(T,w,s) генерирует треугольный импульс с длительностью w и перекосом, заданным третьим входным параметром s, который должен лежать в диапазоне от -1 до 1. При s=0 генерируется симметричный треугольный импульс. Генерирует треугольный импульс с длительностью w и перекосом, заданным третьим входным параметром s, который должен лежать в диапазоне от -1 до 1. При s=0 генерируется симметричный треугольный импульс.

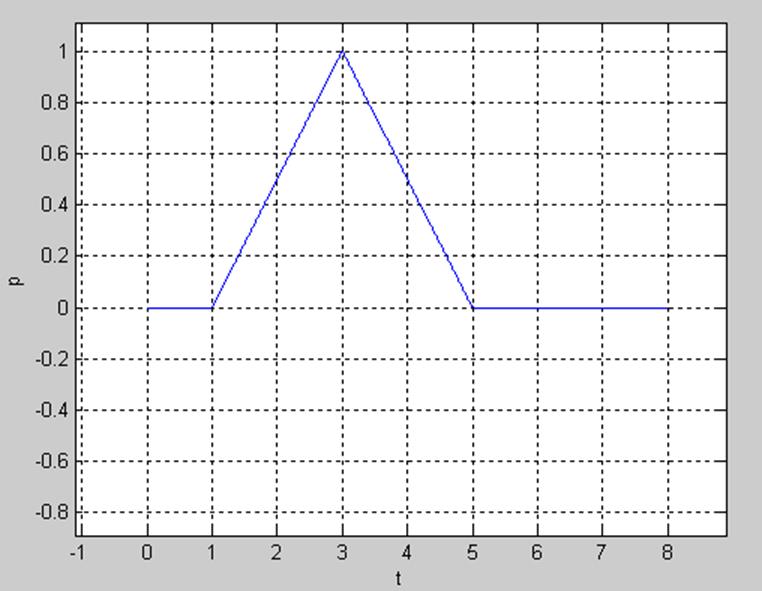
Рис. 6

Треугольный импульс

6.  Cоздание файл-функций и script-файлов в среде Matlab

6.1  Cоздание файла-функции для  вычисления интеграла от функции  на интервале , используя метод прямоугольников.

Листинг файл-функции:

function I=integral(N)

%Вычисление приближенного значения интеграла методом %прямоугольников, определенного от 0 до 2*pi

% нет синтаксиса обращения

a=0;

b=0,2*pi;

h=(b-a)/N;          %высота прямоугольника

c=0:2*pi/N:2*pi;   

y=sin(c).^2;       %ширина прямоугольника

I=h*sum(y)

Команда:

I=integral(100,0,2*pi);

Результат: I =    3.1416

6.2.  Создание script-файла для  вычисления интеграла от функции  на интервале , используя метод прямоугольников

Листинг файла-скрипта:

% Вычисление приближенного значения определенного интеграла c заданным числом точек разбиения

N=input('Введите число точек разбиения= ');

I=integral(N)

Команды:

ведите число точек разбиения= 100

Введите a=0

Введите b=2*pi

Результат:  I =   3.1416

7.  Генерирование и построение графиков шума,  сигнала и их суммы.

X=randn(50,1)

Листинг файла-скрипта

   for m=1:50

   x(m)=randn(1); %генерирование 50 значений случайного шума с      

   помощью функции  randn()

   y(m)=2*m*(0.9^m);

   end;

   z=x+y;

   subplot(1,3,1); %Вывод графиков

   plot(y);

   title('График функции 2*m*(0.9^m)');

   xlabel('m');

   ylabel('y(m)');

   legend('2*m*(0.9^m)');

   subplot(1,3,2);

   plot(x);

   title('Случайные числа');

   legend('rand');

   xlabel('m');

   ylabel('x(m)');

subplot(1,3,3);

   plot(z);

   title('Сумма');

   xlabel('m');

   ylabel('z(m)');

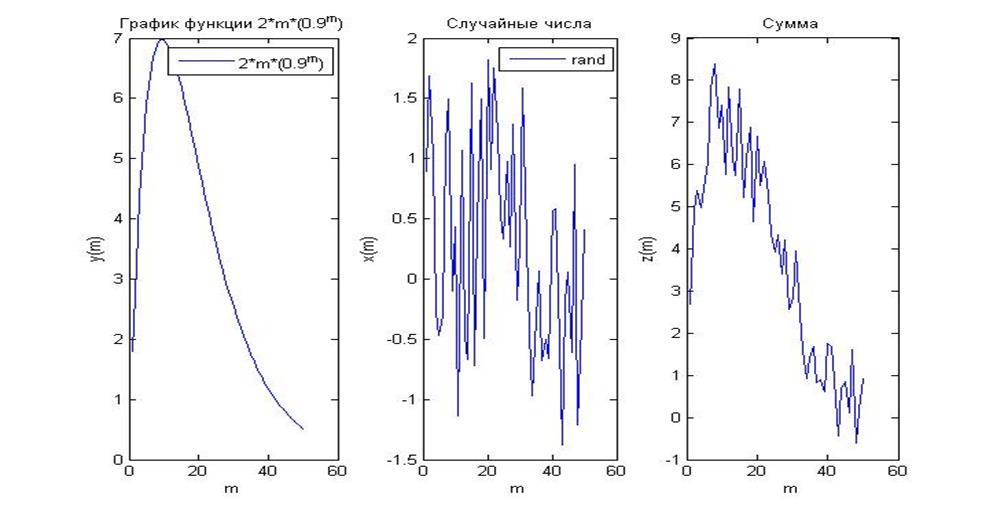
Рис. 7. Графики функций

8.  Генерирование дискретных сигналов: единичного импульса, ступенчатого  и пилообразного.

Листинг скрипт-файла:

% Процедура генерирования и построения графиков

% единичного импульса (imp), ступенчатого (step)

% и пилообразного (ramp) сигналов

L = input('Введите длину сигнала= '); %Ввод значения длины сигнала

n = 1:L;

FT = input(' Введите частоту отсчетов = '); %Ввод значения частоты отсчетов

T = 1/FT; %Период сигнала

imp = [1 zeros(1,L-1)] %заполняем массив imp нулями (кроме 1-го элемента - единичный импульс)

% вариант    imp = (n==1);

step = ones(1,L); %Формируем массив единиц размера 1 х L.

ramp = (n-1).*step;  %перемножаем массивы (отсчеты)*(шаг) из за смещения на 1 получается пилообразный сигнал

%Выводим графики

subplot(3,1,1);

stem(n-1,imp);

set(gca,'FontName','Arial Cyr', 'FontSize',10)

xlabel([' Интервал отсчетов',num2str(T), ' сек']);ylabel('Амплитуда');

subplot(3,1,2);

stem(n-1,step);

set(gca,'FontName','Arial Cyr', 'FontSize',10)

xlabel(['Интервал отсчетов ',num2str(T), ' сек']);ylabel('Амплитуда');

subplot(3,1,3);

stem(n-1,ramp);

set(gca,'FontName','Arial Cyr', 'FontSize',10)

xlabel(['Интервал отсчетов',num2str(T), ' сек']);ylabel('Амплитуда');

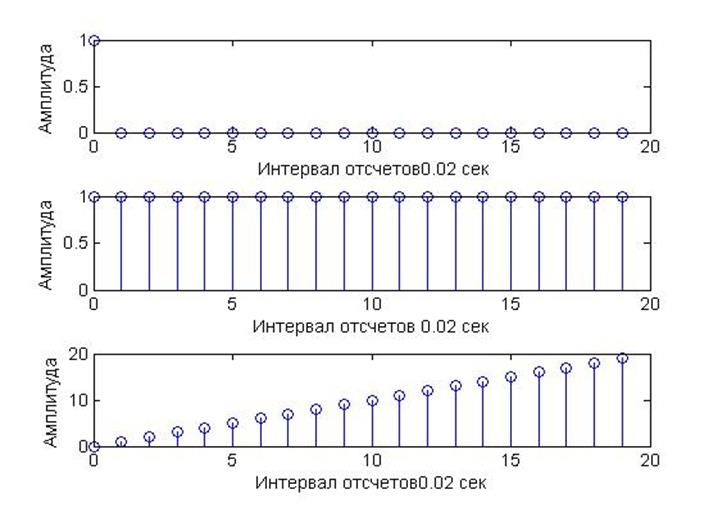
Рис.8

9.  Процедура формирования и проигрывания последовательности нот

%  Процедура формирования и проигрывания последовательности нот

%  Каждая последующая нота имеет частоту, большую в 21/12 раз, чем предыдущая

fs = 8192;         % частота отсчетов

t = 0:1/fs:0.4;    % длительность каждой ноты

tspace = .05;          % длительность паузы между нотами

fr = 2^(1/12);        % отношение частот соседних нот

%Частоты нот

A4 = 440;                   % Частота ноты ЛЯ первой октавы - опорная нота

B4 = A4*fr^2;               % Частота ноты СИ первой октавы

C5 = A4*fr^3;               % Частота ноты ДО второй  октавы

C4 = A4*fr^(-9);

D4 = A4*fr^(-7);

E4 = A4*fr^(-5);

F4 = A4*fr^(-4);

G4 = A4*fr^(-2);

xspace = zeros(size(tspace));

%    формирование вектора нот и пауз между ними

x = [cos(C4*2*pi*t),xspace, cos(D4*2*pi*t),xspace,cos(E4*2*pi*t),...

xspace,cos(F4*2*pi*t),xspace,cos(G4*2*pi*t),xspace,...

cos(A4*2*pi*t),xspace,cos(B4*2*pi*t),xspace,cos(C5*2*pi*t)];

sound(x,fs);   % прослушивание вектора x

10. Написание  файл – функции [x, t] =  harmonic(omega0, omegas, dur) для генерирования синусоидального сигнала.

Листингфайл-функции:

function [x,t]=harmonic(omegao,omegas,dur)

%Функция генерирования синусоидального сигнала

 Ts = 2*pi/omegas;

 t = 0: Ts: dur;

 x = cos(omega0*t);

Последовательность команд

(используем функцию harmonic для построения графиков гармоник)

[x,t]=harmonic(2*pi*261.63, 2*pi*8192, 0.01);

subplot(3,1,1)

plot(t,x)

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('cos(2*pi*261.63*t)')

ylabel('do(t)');

[x,t]=harmonic(2*pi*880, 2*pi*8192, 0.01);

subplot(3,1,2);

plot(t,x);

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('cos(2*pi*880*t)')

ylabel('lya(t)');

[z,t]=harmonic(2*pi*440, 2*pi*8192, 0.01);

y = 0.5*z + x;

subplot(3,1,3);

plot(t,y);

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('0.5*cos(2*pi*440*t)+cos(2*pi*880*t)')

ylabel('y(t)');

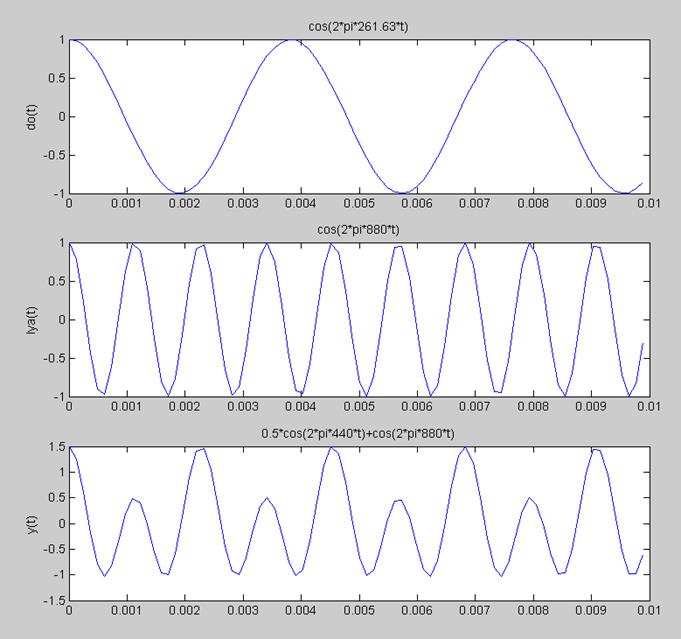
Рис.9 Графики косинусоидального сигнала

Выводы:

Файл-скрипт – это последовательность команд для matlab, которые сохранены в виде файла, подобно макросу.

Файл-функция – последовательность команд  оформленная по определенным правилам, являющаяся исполняемой командой для matlab.

Нота – звуковая волна (гармоническое колебание определенной частоты).

В результате выполнения работы были приобретены практические навыки работы в среде MATLAB, а именно:

-  генерирования непрерывных и дискретных по времени сигналов;

-  построения графиков сигналов;

-  написания файл-функций и script-файлов.