Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра ССОД
Дисциплина «Теория и обработка сигналов»
Лабораторная работа № 6
ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ СИГНАЛОВ
ВАРИАНТ №1
Выполнил: Преподаватель:
Пархоменко А.А. доц. Щетинин Ю.И.
Группа: АТ-53
Новосибирск, 2007
Цель работы:изучение сущности и моделей дискретизации (квантования по времени) сигналов и методов восстановления непрерывных сигналов по отсчетам.
1) Сгенерировать пример непрерывного и дискретного сигналов в среде Matlab и построить их графики.
Далее представлен М-файл с помощью которого были сгенерированы сигналы и построены их графики.
t=0:0.01:8;
x=sin(t);
n=0:8;
x1=sin(n);
subplot(121), stem(n,x1),
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Дискретный сигнал'), xlabel('Отсчеты')
subplot(122), plot(t,x),
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title('Непрерывный сигнал'), xlabel('Время, сек')
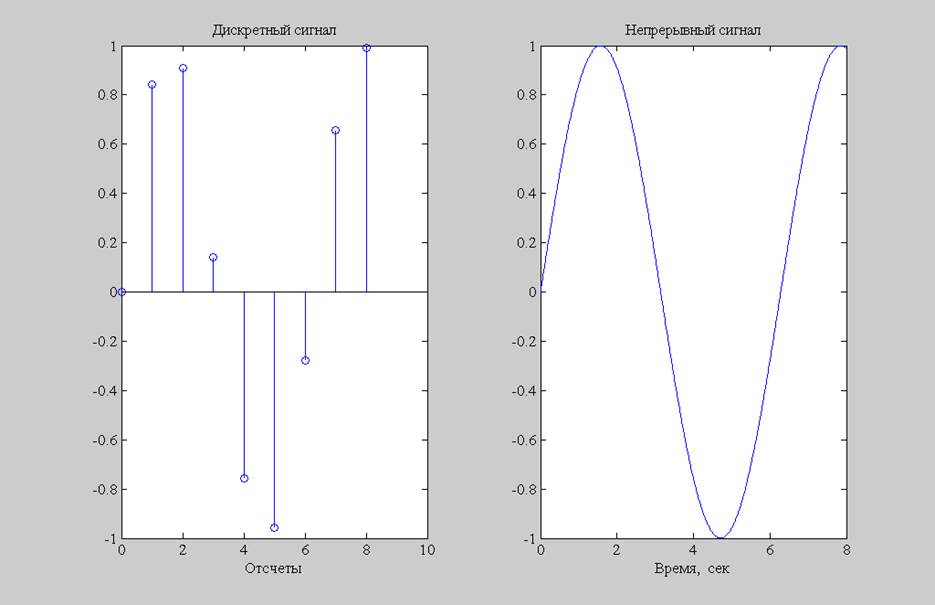
Рис. 1. Графики: а) дискретный сигнал sin[n]; б) непрерывный сигнал sin(t)
2) Для
непрерывного сигнала ![]() сгенерировать последовательности x[n]при нескольких частотах (3…4
значения) отсчетов. Построить графики дискретных сигналов. Сделать вывод о
предельной (критической) частоте отсчетов, достаточной для восстановления
косинусоидального сигнала. Пример файла-сценария представлен в Приложении 1.
сгенерировать последовательности x[n]при нескольких частотах (3…4
значения) отсчетов. Построить графики дискретных сигналов. Сделать вывод о
предельной (критической) частоте отсчетов, достаточной для восстановления
косинусоидального сигнала. Пример файла-сценария представлен в Приложении 1.
Далее представлены М-файлы (на основе Приложения 1) с помощью которых были получены графики.
%М-файл где частота дискретизации = 2000Гц
f=1000; % Частота
Fd=2000; T=1/Fd; % Частота и период отсчетов
t=0:T:60*T; y=cos(2*pi*f*t);
figure(1)
plot(t,y,'-ok')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title(' Дискретизация косинусоидального сигнала, частота дискретизации = 2000Гц')
xlabel(' Время (сек)')
axis([0,40*T,-2,2])
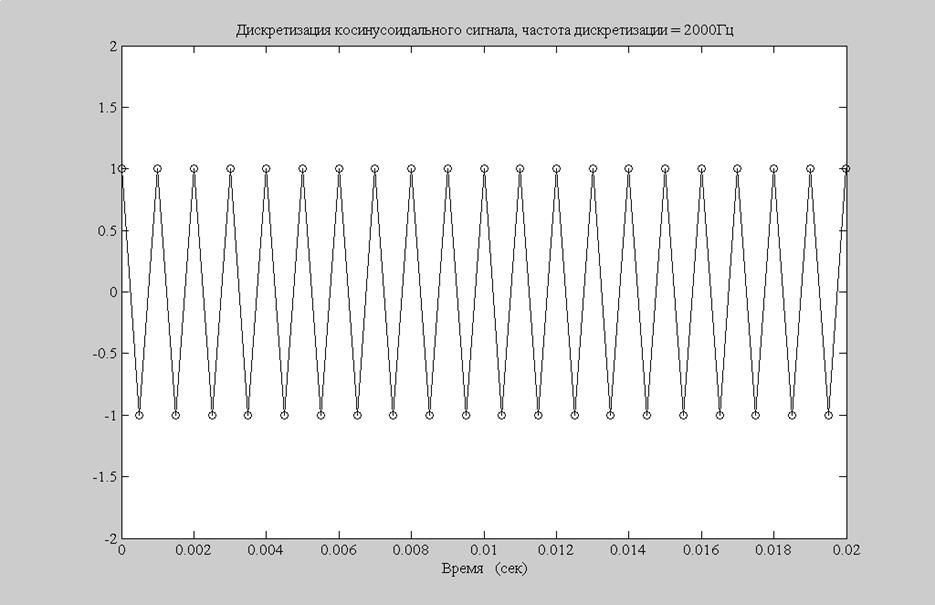
Рис.2. График дискретного сигнала при частоте отсчетов 2000 Гц
%М-файл где частота дискретизации = 1500Гц
f=1000; % Частота
Fd=1900; T=1/Fd; % Частота и период отсчетов
t=0:T:60*T; y=cos(2*pi*f*t);
figure(2)
plot(t,y,'-ok')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title(' Дискретизация косинусоидального сигнала, частота дискретизации = 1000Гц')
xlabel(' Время (сек)')
axis([0,40*T,-2,2])
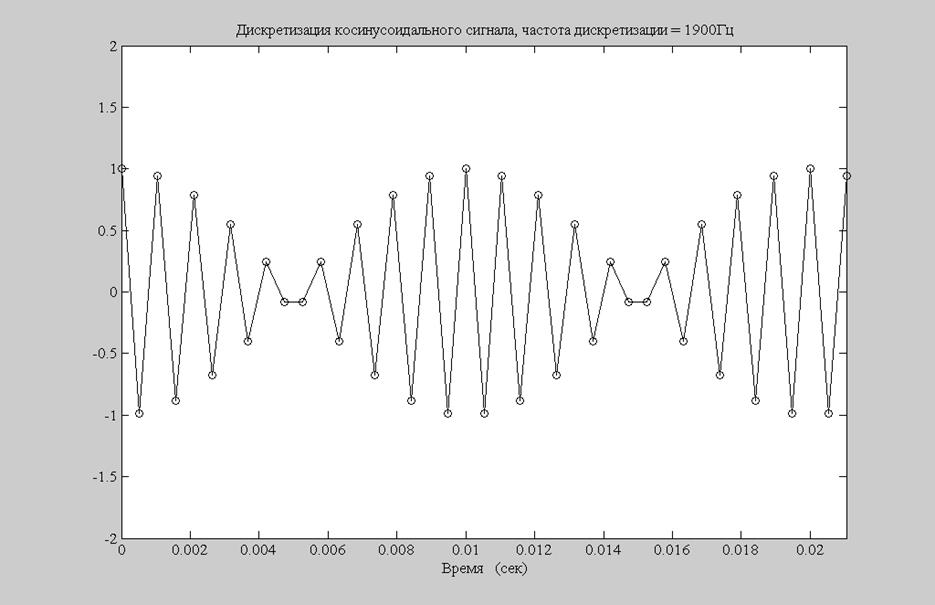
Рис.2. График дискретного сигнала при частоте отсчетов 1900 Гц
%М-файл где частота дискретизации = 10000Гц
f=1000; % Частота
Fd=10000; T=1/Fd; % Частота и период отсчетов
t=0:T:60*T; y=cos(2*pi*f*t);
figure(3)
plot(t,y,'-ok')
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12);
title(' Дискретизация косинусоидального сигнала, частота дискретизации = 10000Гц')
xlabel(' Время (сек)')
axis([0,40*T,-2,2])
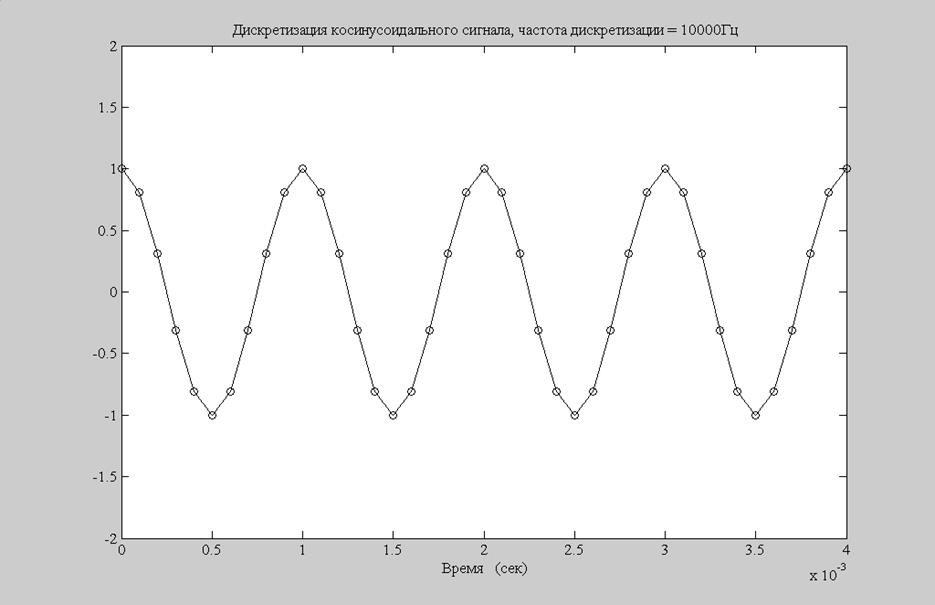
Рис.4. График дискретного сигнала при частоте отсчетов 10000 Гц
По результатам видно, что критическая частота отсчетов =
2кГц. Т.к. частота гармонического сигнала = 1000Гц, то для правильного
восстановления сигнала нужно чтобы частота Найквиста была ![]() частоты гармонического сигнала.
частоты гармонического сигнала.
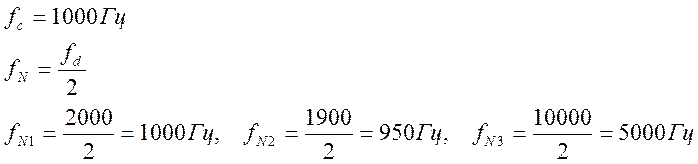
3) С использованием созданной ранее пользовательской
функции
[x, t] = harmonic(omega0, omegas,
dur) сгенерировать гармонические
сигналы длительностью 1с, частотой отсчетов 8192 Гц и частотами 1000, 3000,
4000, 5000 и 6000 Гц. Построить графики (первые 100 отсчетов) сигналов для частот
1000 и 6000 Гц.
С помощью команды sound() прослушать
звучание сгенерированных тональных сигналов. Во всех ли случаях повышается
частота звука с увеличением частоты сигнала? Как это можно объяснить с
помощью теоремы отсчетов?
Далее представлен М-файл с помощью которого были построены графики сигналов с частотой 1000 и 6000 Гц, а также были прослушаны звучания сигналов с частотами 1000, 3000, 4000, 5000, 6000 Гц.
[y1,t]=harmonic(2*pi*1000,2*pi*8192,1);
figure(1)
subplot(2,1,1),plot(t(1:100),y1(1:100)),grid,
axis([min(t(1:100)) max(t(1:100)) min(y1(1:100)) max(y1(1:100))]);
xlabel ('t, sec'),ylabel ('y1'),title (' harmonic with 1000Hz');
sound(y1);
hold on
[y3,t]=harmonic(2*pi*3000,2*pi*8192,1);
sound(y3);
[y4,t]=harmonic(2*pi*4000,2*pi*8192,1);
sound(y4);
[y5,t]=harmonic(2*pi*5000,2*pi*8192,1);
sound(y5);
[y6,t]=harmonic(2*pi*6000,2*pi*8192,1);
subplot(2,1,2),plot(t(1:100),y6(1:100)),grid,
axis([min(t(1:100)) max(t(1:100)) min(y6(1:100)) max(y6(1:100))]);
xlabel ('t, sec'),ylabel ('y6'),title (' harmonic with 6000Hz');
sound(y6);
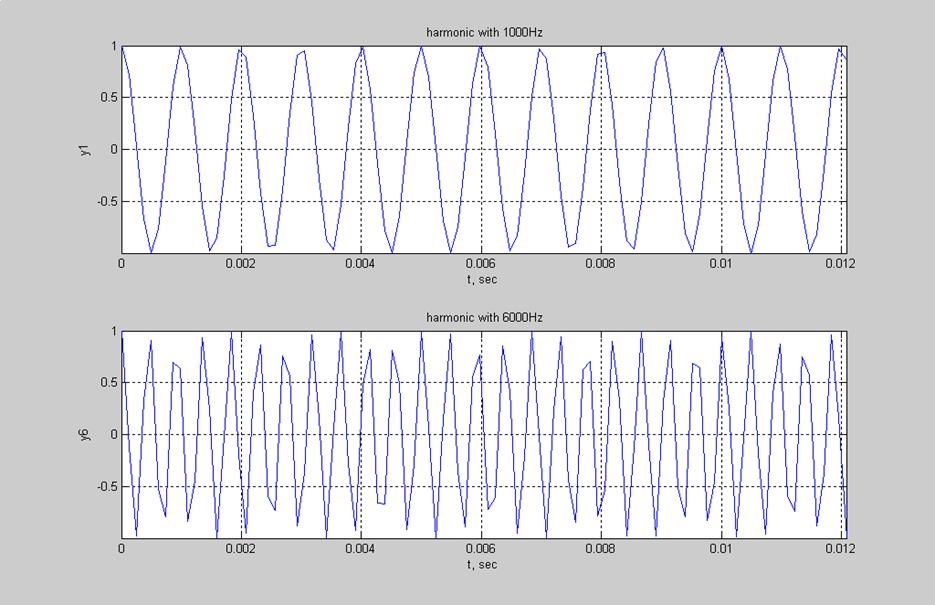
Рис.5. Графики гармонических сигналов с частотой 1000Гц и 6000Гц.
Частота звука повышается при частотах с 1000 до 4000(включительно), при частотах 5000 и 6000 Гц частота звука понижается. При генерировании сигнала с частотой больше, чем частота Найквиста (в данном примере 4096Гц), получается звук с более низкой частотой, чем у сигналов частоты которых удовлетворяют частоте Найквиста (у таких сигналов идет повышение частоты звука при увеличении частоты гармонического сигнала).
4) Используя файл – сценарий из приложения 2, получить графики амплитудных спектров сигналов из предыдущего пункта. Объяснить характер полученных спектров.
Далее представлен М-файл (основанный на Приложении 2) с помощью которого были построены графики амплитудных спектров.
f= input('Введите частоту сигнала в Гц f = ');
fs=8192;
dur=1;
[x,t]=harmonic(2*pi*f,2*pi*fs,dur); %сигнал
Fmax=fs;
df=1/dur;
f=-Fmax/2:df:Fmax/2; % частотная шкала
X=fft(x,length(f));
X1=fftshift(X);
subplot(211), plot(t(1:50),x(1:50),'-o')
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
legend('Сигнал'), xlabel('Время, с')
subplot(212), plot(f,abs(X1)*1/fs)
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
legend('Амплитудный спектр'), xlabel('Частота, Гц')
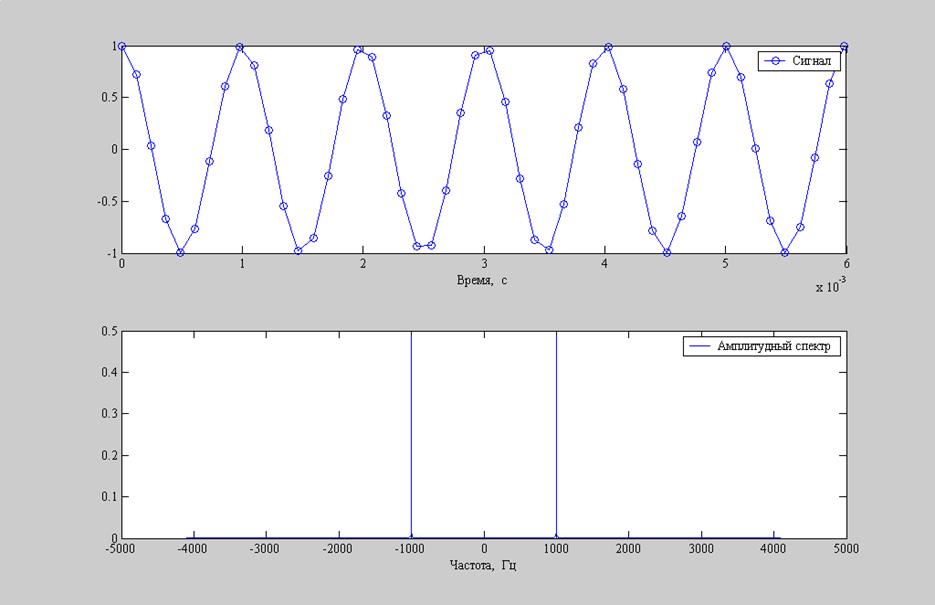
Рис.6. Графики: а) гармонический сигнал с частотой 1000Гц; б) амплитудный спектр гармонического сигнала.
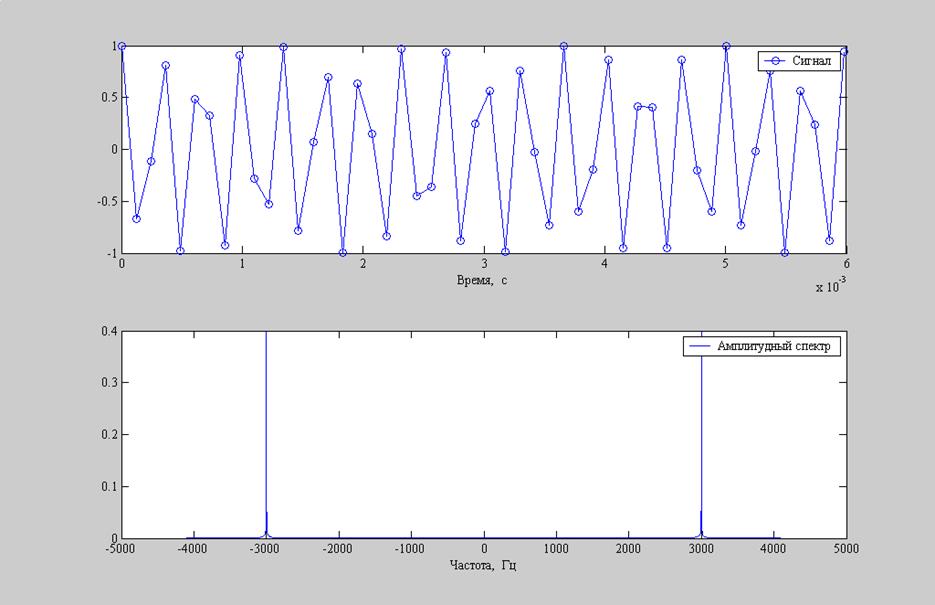
Рис.7. Графики: а) гармонический сигнал с частотой 3000Гц; б) амплитудный спектр гармонического сигнала.
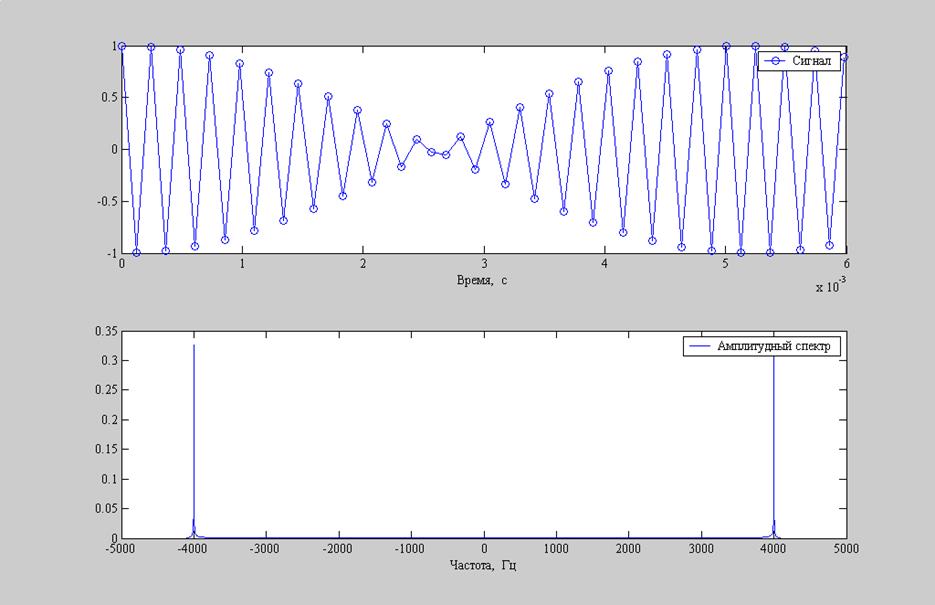
Рис.8. Графики: а) гармонический сигнал с частотой 4000Гц; б) амплитудный спектр гармонического сигнала.
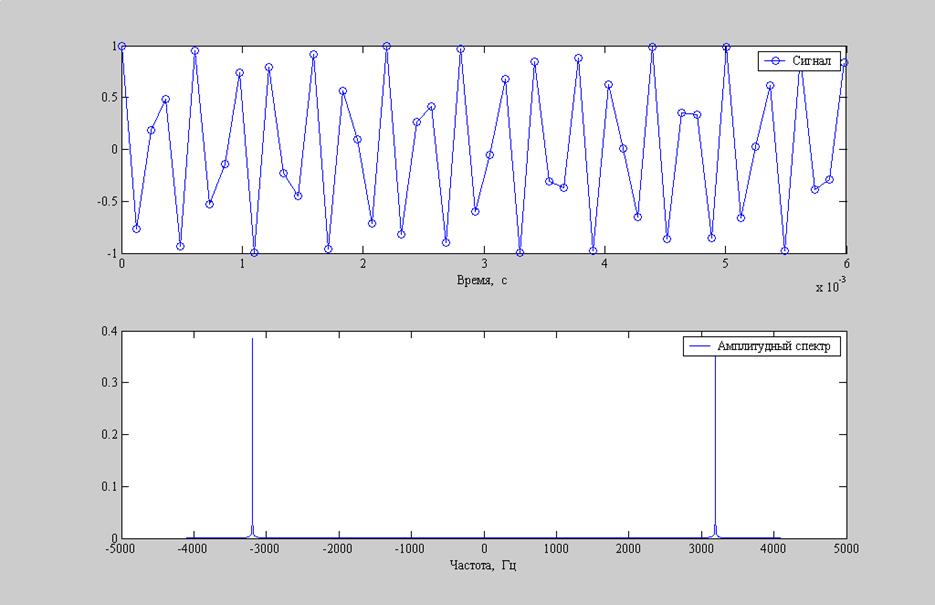
Рис.9. Графики: а) гармонический сигнал с частотой 5000Гц; б) амплитудный спектр гармонического сигнала.
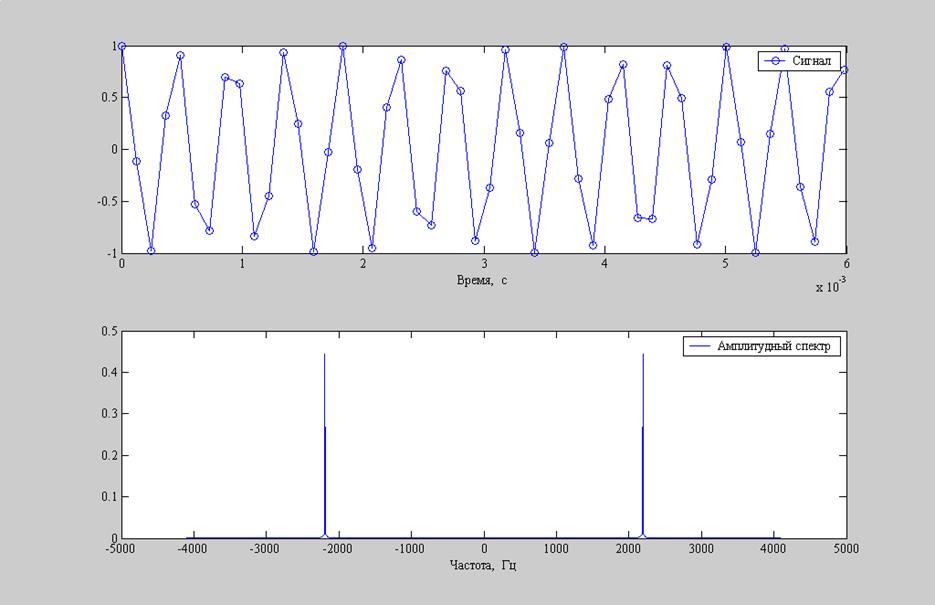
Рис.10. Графики: а) гармонический сигнал с частотой 6000Гц; б) амплитудный спектр гармонического сигнала.
Исходя из теоремы отсчетов ![]() .
Это условие выполняется для гармонических сигналов с частотами 1000, 3000 и
4000Гц. И как видно из графиков амплитудного спектра сигналов max амплитуда достигается на частотах
.
Это условие выполняется для гармонических сигналов с частотами 1000, 3000 и
4000Гц. И как видно из графиков амплитудного спектра сигналов max амплитуда достигается на частотах ![]() и
и
![]() . Для гармонических сигналов 5000 и
6000Гц
. Для гармонических сигналов 5000 и
6000Гц ![]() , т.е.
происходит наложение спектров. Тем самым max амплитуда на графиках спектрах этих сигналов достигается на
частотах
, т.е.
происходит наложение спектров. Тем самым max амплитуда на графиках спектрах этих сигналов достигается на
частотах ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.