Z-преобразование и дискретно-временное преобразование Фурье: Методические рекомендации по выполнению лабораторной работы

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»,     6 - й  семестр

ЛАБОРАТОРНАЯ  РАБОТА  № 9

Z - преобразование 

и  дискретно – временное  преобразование  Фурье

Цель работы:Изучение  Z – преобразования и дискретно – временного преобразования  Фурье (ДВПФ),  их вычисления  в среде Matlab.

Задание и порядок выполнения работы.

1.  Ознакомьтесь с теоретическими сведениями по Z – преобразованию и дискретно – временному преобразованию Фурье, изложенными в учебной литературе, например, [1] стр. 32 – 48 или  [2], стр. 143 – 147 и в лекционном курсе.

2.  Запишите и прокомментируйте  выражения прямого и обратного Z - преобразования.  Найдите аналитически  Z – преобразование и области его сходимости для сигналов
а)  x[n] = δ[n],

б)  x[n] = u[n],
в)  x[n] = sin ω₀n,

г)  .

3.  С помощью функции   ztrans()  Matlab найдите и запишите в обычной математической форме  Z – преобразования сигналов (последовательностей):   

     а)   x[n] = aⁿ cos ωn,
     б)   x[n] = n² e²ⁿ,

     в)   x[n] = cos² n.
4.  Используя функцию  iztrans()  Matlab определите сигнал во временной области (оригинал) по его Z – преобразованию
     а)  ,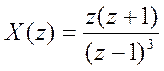

б)  .
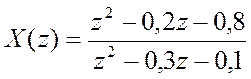Сделайте заключение  по использованию и возможностям

  функций  ztrans()  и iztrans(). 

5.  С помощью функции residuez() разложите заданную функцию рационального  Z – преобразования (индивидуальное задание,  Приложение 1) на простейшие (элементарные)  дроби. Для более подробных сведений см. файл «Разложение на простейшие дроби» в папке «Учебно-справочные материалы» по курсу.

Используя это разложение,  найдите аналитически  обратное Z - преобразование.  C помощью функции  iztrans() проверьте результат.

6.  Решите с помощью Z– преобразования линейное разностное уравнение с постоянными коэффициентами (вариант – по индивидуальному заданию,  Приложение 3).
       Решение заключается в применении Z– преобразования к разностному уравнению с использованием свойств линейности  и временного сдвига. В результате получается  линейное алгебраическое уравнение относительно Z - изображения искомой функции. Обратное Z– преобразование дает искомое решение во временной области. Постройте график найденного решения. Проверьте его правильность подстановкой в исходное уравнение.

     Пример соответствующего решения представлен в Приложении  4.
См. также   «Решение разностных уравнений» в папке  «Учебно - справочные материалы » курса.

7.  Запишите и прокомментируйте выражения прямого и обратного дискретно-временного преобразования Фурье (ДВПФ).   Как связаны ДВПФ и Z – преобразование?
     Аналитически вычислите Z – преобразование  и ДВПФ сигнала
                                  
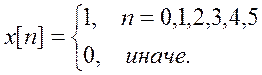
Преобразуйте  результат к окончательному виду с использованием выражения  суммы конечной геометрической прогрессии и формулы Эйлера.
8.  Изучите программу файл – функции вычисления ДВПФ, представленную в Приложении  5.

      Найдите с помощью этой программы  ДВПФ  сигналов
а)     x₁[n] = e ^-0,5n,
б)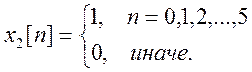    

в)       

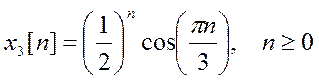
для значения  размера преобразования  M = 64.
       Постройте и объясните графики сигналов и амплитудного и фазового спектров этих сигналов.

9. Ознакомьтесь с программой, приведенной в Приложении 6. Эта программа иллюстрирует  (не доказывает!)  основные  из свойств ДВПФ.
 Сформулируйте каждое свойство,  исполните программу и объясните результаты применительно к каждому свойству.

10.  Составьте отчет по лабораторной работе. В отчете должны быть представлены

§  титульный лист,

§  название и цель работы,

§  формулировки пунктов работы, необходимые формулы и выражения,   .m – файлы,   графики, комментарии, выводы.

Литература

1.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.2.

2.  Сергиенко А.Б.  Цифровая обработка сигналов. СПб.: Питер, 2003.

Web-ресурсы

1.  http://www.jhu.edu/~signals/dtftprops/indexDTFTprops.htm

Контрольные вопросы и упражнения

1.  Запишите и объясните выражения прямого и обратного Z – преобразований.

2.  Какова связь между Z– преобразованием и преобразованием Лапласа?

3.  Найдите Z – преобразования сигналов
а) 
б) 

4.  Используя свойство временного сдвига в Z – области, определите
Z – преобразование от  .

5.  С помощью свойства дифференцирования в z – области найдите Z - преобразование  от  .

6.   В среде Matlab определите Z – преобразование сигнала

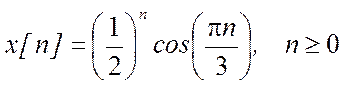
и обратное Z – преобразование  для  .

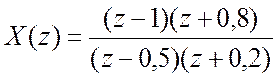7.  С помощью Z – преобразования найдите решение разностного уравнения
.

8.  Укажите основные области практического применения Z - преобразования.

9.  Запишите и объясните выражения прямого и обратного ДВПФ.

10. Докажите периодичность ДВПФ.  Чему равен период ДВПФ для интервала отсчетов ?

11. Какова связь Z – преобразования и ДВПФ?   Где находится область определения ДВПФ  в z– области?

12. Как можно  вычислить ДВПФ в Matlab?

13.  Вычислите ДВПФ для  .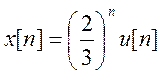

14.  Докажите свойство свертки ДВПФ. Объясните, как это свойство можно использовать для вычисления дискретной свертки.

15.   Можно ли вычислять ДВПФ с помощью функции fft()  Matlab?

Приложение 1.   Варианты индивидуальных заданий  к  п. 5.

1.       .

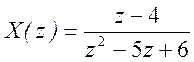2.       .

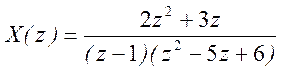3.      

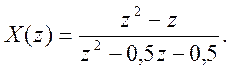
4.          .

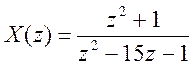5.       .

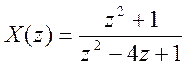6.       .

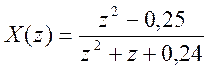7.       .

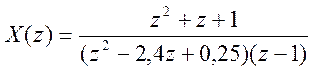8.       .

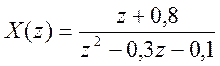9.       .

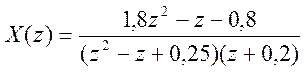10.     .

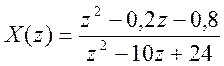11.   .

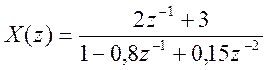12.    .

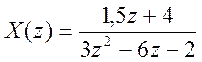Приложение 2.  Свойства линейности и временного сдвига   Z – преобразования.

 1.  Свойство линейности
     

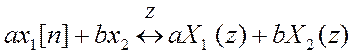
2.  Свойство временного сдвига
а)  ,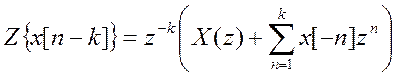

б)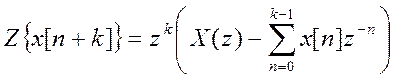 

Приложение 3.   Варианты индивидуальных заданий к п. 6.

1.       .

2.       .

3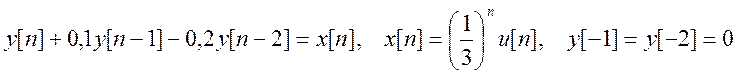

4.                

5.       .

6.       .

7.       .

8.       .

9.       .

10.     .

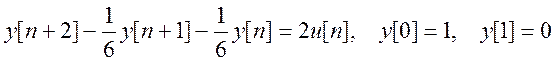11.        ,     .

12.        ,         

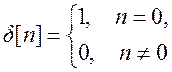
Приложение 4.  Пример решения линейного разностного уравнения.

Уравнение  .

Беря  Z- преобразование от уравнения,  с учетом свойства временного сдвига получаем          .  

Z – преобразование  входного сигнала  .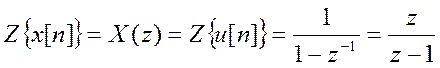

Отсюда    .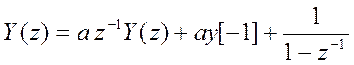

Решение уравнения в Z – области

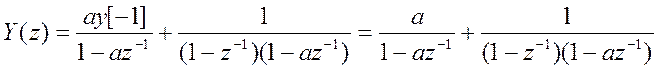
Обратное Z-преобразование от первого слагаемого правой части

.

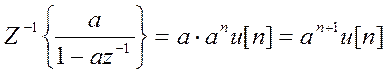Для вычисления обратного Z – преобразования  от 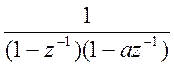 разложим эту дробь  на простейшие  дроби

.

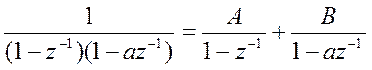Найдем коэффициенты А и В – числители дробей  

,         .

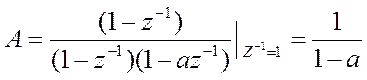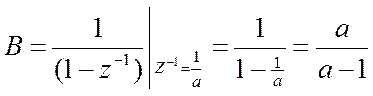Обратные Z- преобразования от отдельных дробей

,             

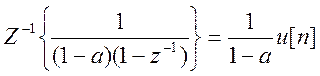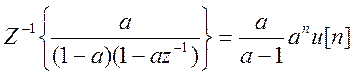
Поэтому  решение уравнения

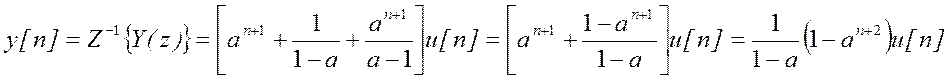Проверка решения:

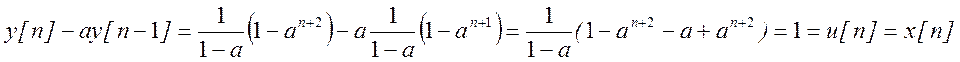Другой способ проверки:

Из заданного уравнения 

непосредственной  подстановкой для    получаем

,

   и т.д.

Те же значения получаем по выражению 

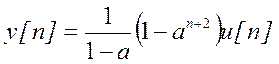 при 

Приложение 5.   Файл – функция вычисления ДВПФ

function [X,w] = DTFT(x,M)

% Функция вычисляет значения DTFT от вектора x.

% Обращение

%             [X,w] = DTFT(x,0)

% здесь X - вектор значений DTFT,

% w - вектор угловых частот.

% Если нужно вычислить DTFT с M значениями частоты,

% используется обращение

%             [X,w] = DTFT(x,M)

% Этот вариант используется, когда размер вектора x 

% меньше  размера вектора частот w,

% при этом x дополняется нулевыми значениями

N = max(M,length(x));

% Приведение FFT к размеру 2^m

N = 2^(ceil(log(N)/log(2)))

% Вычисление  fft

X = fft(x,N);

% Вектор  частот

w = 2*pi*( (0:(N-1))/N );

w = w - 2*pi*(w>=pi)

% Сдвиг FFT к интервалу от -pi до +pi

X = fftshift(X);

w = fftshift(w);

Приложение 6.  Процедура  (скрипт – файл)  иллюстрации свойств ДВПФ

N = 128; %  Длина сигналов

k = 0:N-1;

gamma = -0.1;

g = exp(gamma*k);

% g - экспоненциальная функция

h = sin(2*pi*k/(N/4));

figure(1)

subplot(211),stem(k,g)

legend('exp(gamma*k)')

subplot(212),stem(k,h)

legend('sin(2*pi*k/(N/4))')

% h - синусоидальная последовательность с периодом = N/4

% вычисление ДВПФ

[G,w] = DTFT(g,512);

[H,w] = DTFT(h,512);

figure(2)

subplot(211), plot(w,abs(G))

subplot(212), plot(w,abs(H))

legend('w=2*pi/32=0,2')

% Свойство линейности

alpha = 0.5;

beta = 0.25;

y = alpha*g+beta*h;

[Y,w] = DTFT(y,512);

% Графики Y и  alpha*G+beta*H для проверки их равенства

figure(3), subplot(211),plot(w,abs(Y))

subplot(212), plot(w,abs(alpha*G+beta*H))

%input(' Для продолжения нажмите любую клавишу')

% Свойство временного сдвига

n0 = 12;

% y2 - последовательность y, сдвинутая на 12 отсчетов

y2 = [zeros([1,n0]) g];

[Y2,w] = DTFT(y2,512);

G0 = exp(-j*w*n0).*G;

% Графики амплитудных спектров

figure(3), subplot(211), plot(w,abs(G0))

subplot(212), plot(w,abs(Y2));

% Свойство изменения масштаба

a=0.1;  % Коэффициент изменения масштаба

g1= exp(gamma*k*a);

figure(4),plot(k,g,k,g1) % Графики во временной области

legend('g','g1')

[G,w] = DTFT(g,512);

G1 = DTFT(g1,512);

% Графики спектров

figure(5), subplot(211), plot(w,abs(G))

subplot(212), plot(w,abs(G1))

% Свойство свертки

y5 = conv(g,h);

[Y5,w] = DTFT(y5,512);

figure(6), subplot(211), plot(w,abs(Y5))

subplot(212), plot(w,abs(G.*H))

% Теорема Парсеваля

val1 = sum(g.*g);

val2 = sum(G.*conj(G))/512;

% Сравнение val1 с  val2

disp('Разность   val1-val2 = ')

disp(val1-val2)

Составил  доцент кафедры ССОД     Щетинин Ю.И.