1) взятие Z-преобразования от уравнения 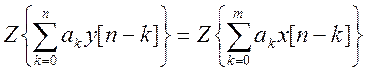 ;
;
2) нахождение решения в z-области ![]() ;
;
3) вычисление обратного Z-преобразования ![]() .
.
7. Вычисление ДВПФ сигнала 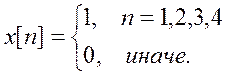 .
.
ДВПФ сигнала имеет вид: 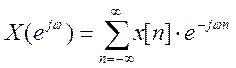
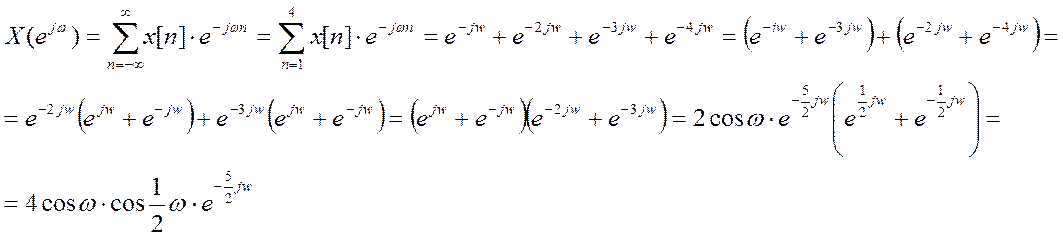
Комментарий: Как видно дискретному сигналу ![]() в соответствие ставится непрерывная
функция
в соответствие ставится непрерывная
функция ![]() . Сигнал представляется в виде суммы
комплексных гармоник с амплитудами равными значениям дискретного сигнала. Т.о.
можно сделать вывод, что ДВПФ - это ряд Фурье по переменной
. Сигнал представляется в виде суммы
комплексных гармоник с амплитудами равными значениям дискретного сигнала. Т.о.
можно сделать вывод, что ДВПФ - это ряд Фурье по переменной ![]() , а коэффициентами этого ряда
являются значения дискретного сигнала.
, а коэффициентами этого ряда
являются значения дискретного сигнала.
8. Вычисление ДВПФ сигналов с помощью средств Matlab:
а) ![]() ,
,
б) 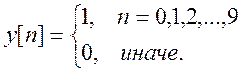
для значения ![]() (значение частоты). Графики
амплитудного и фазового спектров этих сигналов.
(значение частоты). Графики
амплитудного и фазового спектров этих сигналов.
%Функция вычисляет значения DTFT от вектора x,
%w - вектор угловых частот,
%M - значение частоты.
%Когда размер вектора x меньше размера вектора частот w,
%x дополняется нулевыми значениями.
function [X,w] = DTFT(x,M)
N = max(M,length(x));
%Приведение FFT к размеру 2^m
N = 2^(ceil(log(N)/log(2)));
%Вычисление fft
X = fft(x,N);
%Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi);
%Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
а) ДВПФсигнала![]() :
:
n = 0:1:6;
x = exp(-0.5*n);
[X,w] = DTFT(x,64);
subplot(2,1,1)
plot(w,abs(X)),grid
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title(['Амплитудный спектр сигнала {\itx} = {exp}^{-0.5*{\itn}} для n =', num2str(N),
' отсчетов']),
xlabel('w, рад/сек')
subplot(2,1,2)
plot(w,angle(X)),grid
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title(['Фазовый спектр сигнала {\itx} = {exp}^{-0.5*{\itn}} для n =', num2str(N),
' отсчетов']),
xlabel('w, рад/сек')
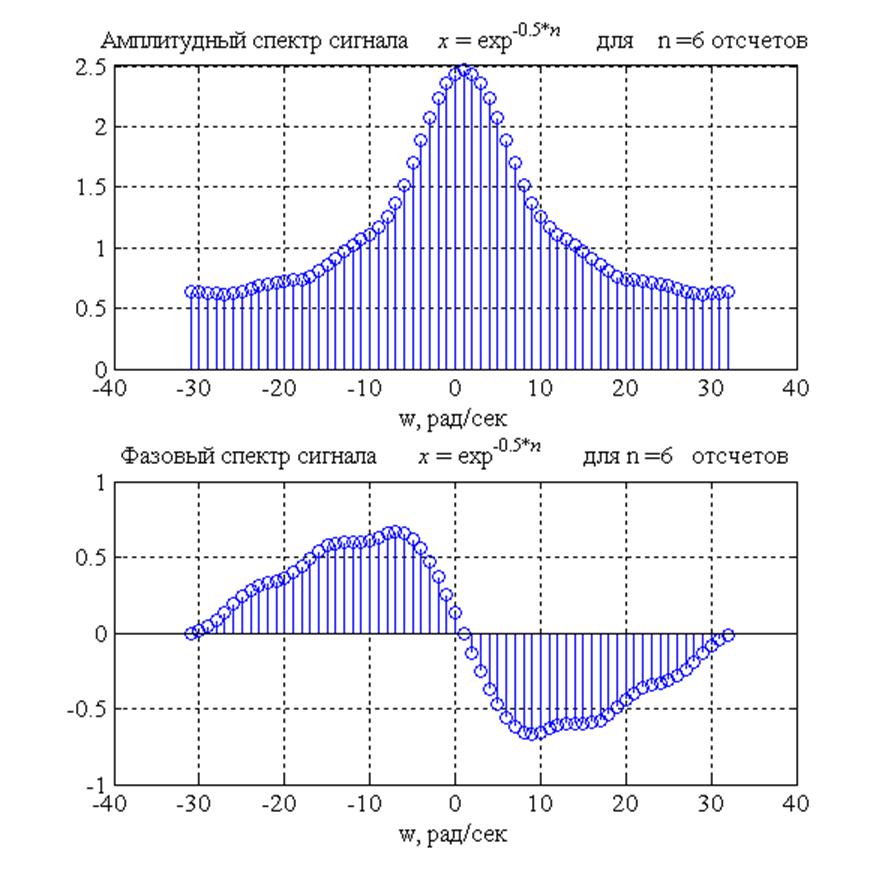
Рис.1. Амплитудный и
фазовый спектры сигнала ![]() , при
, при ![]()
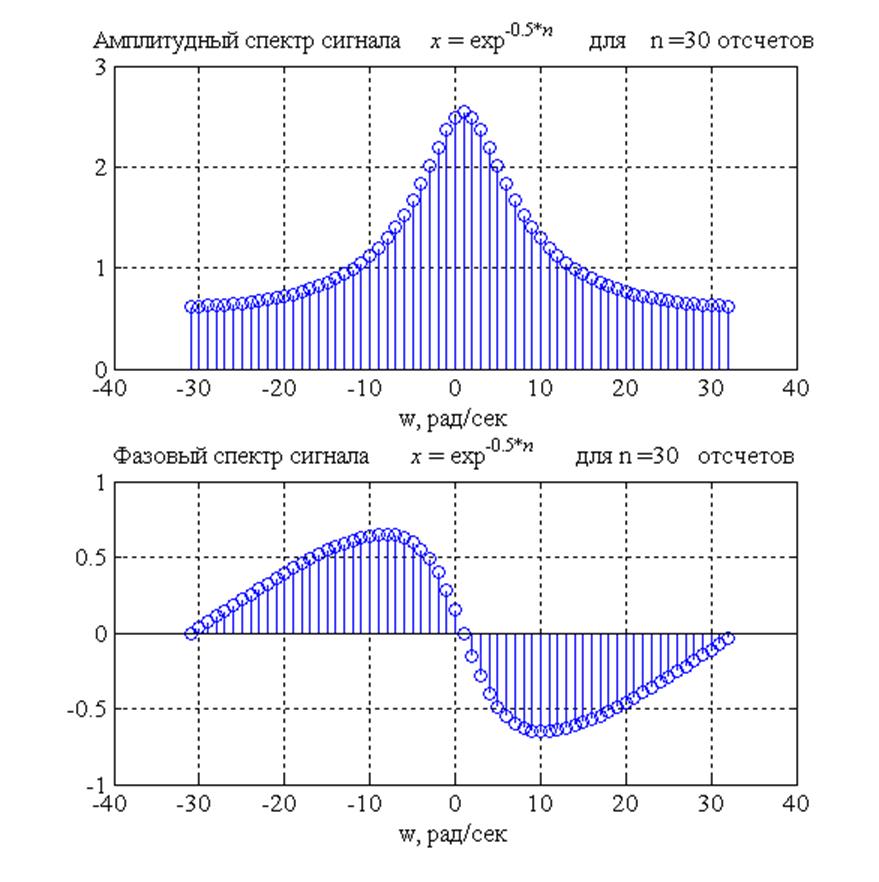
Рис.2. Амплитудный и
фазовый спектры сигнала ![]() , при
, при ![]()
Комментарий: В данном пункте можно увидеть, что
так же, как и для ряда Фурье, с увеличением дискретных значений сигнала
(значений коэффициентов ряда) модуль 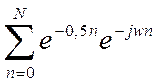 будет сходиться
к модулю предела
будет сходиться
к модулю предела 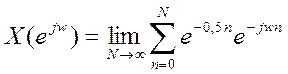 . При
. При ![]() видны колебания в амплитудном
спектре, но уже при увеличении
видны колебания в амплитудном
спектре, но уже при увеличении ![]() до
до ![]() амплитудный спектр сходится к модулю
предела
амплитудный спектр сходится к модулю
предела ![]() и представляет собой гладкую линию
без пульсаций. ДВПФ является периодической функцией с периодом
и представляет собой гладкую линию
без пульсаций. ДВПФ является периодической функцией с периодом ![]() , поэтому достаточным было отобразить
фазовый и амплитудный спектры в интервале
, поэтому достаточным было отобразить
фазовый и амплитудный спектры в интервале ![]() .
Как видно из графиков, амплитудный спектр ДВПФ – чётная функция (график
симметричен относительно оси ординат), а фазовый спектр – нечётная функция
(график симметричен относительно начала координат).
.
Как видно из графиков, амплитудный спектр ДВПФ – чётная функция (график
симметричен относительно оси ординат), а фазовый спектр – нечётная функция
(график симметричен относительно начала координат). ![]() -
дискретная функция,
-
дискретная функция, ![]() - непрерывная функция.
- непрерывная функция.
б)
ДВПФ сигнала 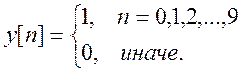 :
:
n=1:9;
x(n)=1;
[X,w]=DTFT(x,64);
t=-31:1:32;
subplot(2,1,1)
stem(t,abs(X)),grid
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title(['Амплитудный спектр сигнала x=1 для n =',num2str(N),' отсчетов']),
xlabel('w, рад/сек')
subplot(2,1,2)
stem(t,angle(X)),grid
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title(['Фазовый спектр сигнала x=1 для n =',num2str(N),' отсчетов']),
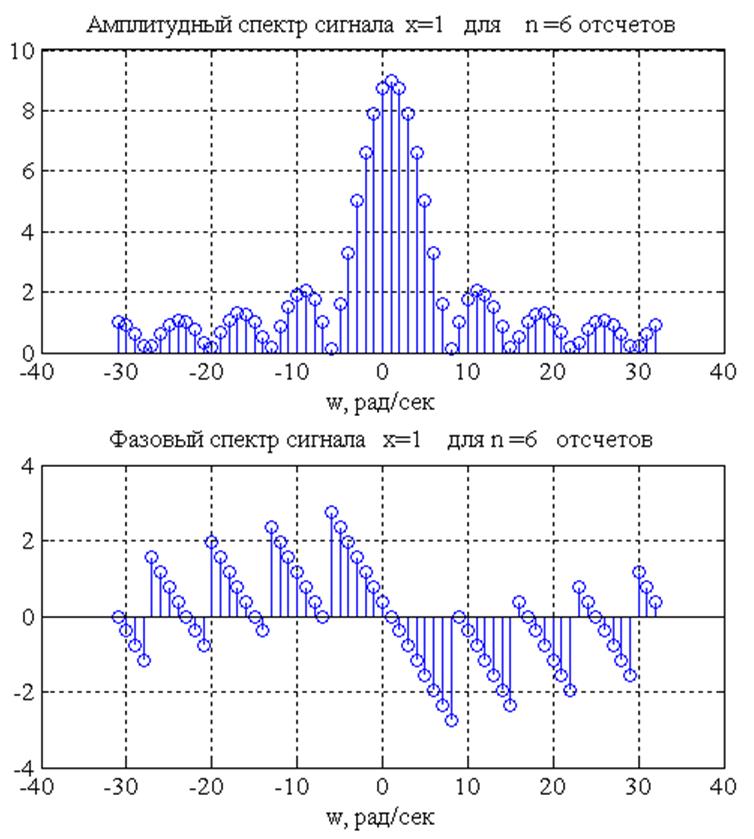 |
Рис.3. Амплитудный и
фазовый спектры сигнала 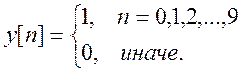
Комментарий: На основании полученного графика
амплитудного спектра дискретного прямоугольного импульса можно сделать вывод,
что ДВПФ этого сигнала представляет собой ![]() функцию
(для непрерывного прямоугольного импульса преобразование Фурье имеет
аналогичный вид, с единственным отличием: график спектральной плотности –
функция непериодическая).
функцию
(для непрерывного прямоугольного импульса преобразование Фурье имеет
аналогичный вид, с единственным отличием: график спектральной плотности –
функция непериодическая).
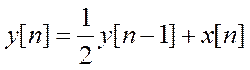 .
. Нахождение частотной характеристики инверсной системы.
![]() :
: ![]()
АЧХ систем. Фильтрация прямоугольного
импульса вначале системой ![]() , а затем её
выход - системой
, а затем её
выход - системой ![]() .
.
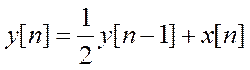
Беря ДВПФ от уравнения, с учётом свойства линейности:
![]() , и временного сдвига:
, и временного сдвига: ![]() , получается:
, получается: 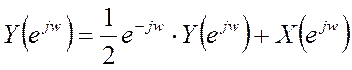 ,
,
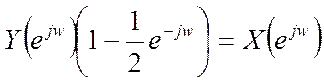
Таким образом, частотная характеристика данной дискретной системы имеет вид:
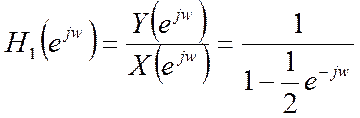 .
.
Частотная
характеристика инверсной системы ![]() такой, что
последовательное соединение её с первой имеет единичную частотную
характеристику, имеет вид:
такой, что
последовательное соединение её с первой имеет единичную частотную
характеристику, имеет вид:
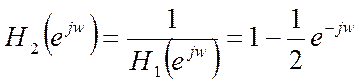 .
.
![]() - вычисляет частотную характеристику
дискретной системы с передаточной функцией
- вычисляет частотную характеристику
дискретной системы с передаточной функцией ![]() .
.
а)
АЧХ системы с частотной характеристикой 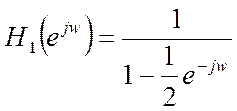 :
:
num = [1];
den = [1,-0.5];
freqz(num,den)
subplot(211)
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title('Амплитудный спектр системы')
subplot(212)
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title('Фазовый спектр системы')
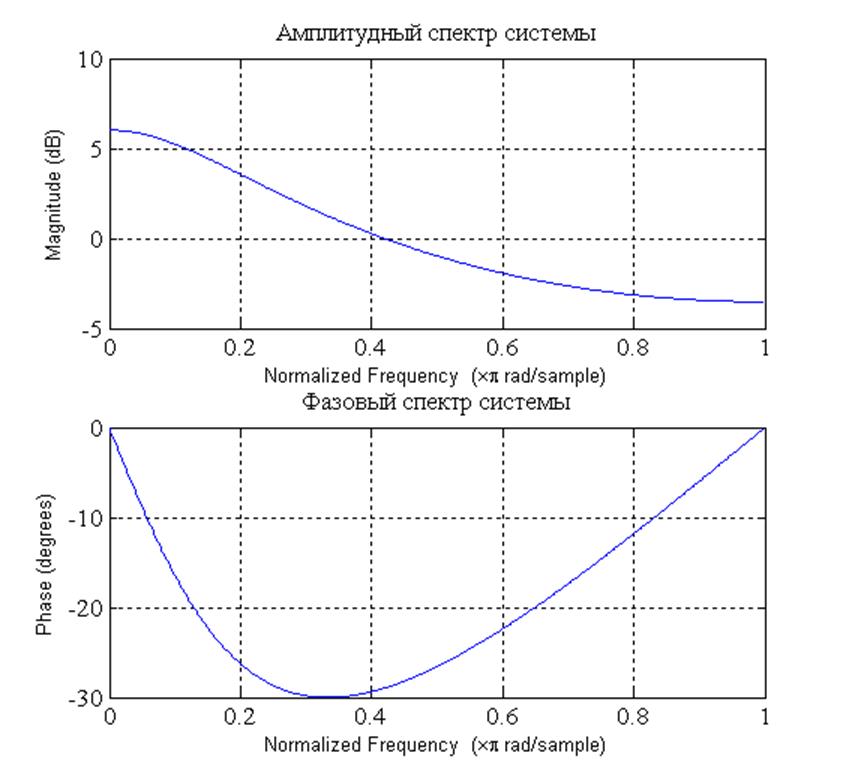
Рис.4. Амплитудный и
фазовый спектры системы с частотной характеристикой 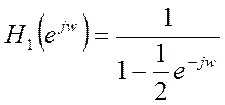
б) АЧХ системы с
частотной характеристикой 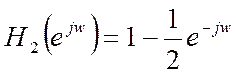 :
:
num = [1,-0.5];
den = [1];
freqz(num,den)
subplot(211)
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title('Амплитудный спектр системы')
subplot(212)
set(gca,'FontName','Times New Roman Cyr','FontSize',12)
title('Фазовый спектр системы')
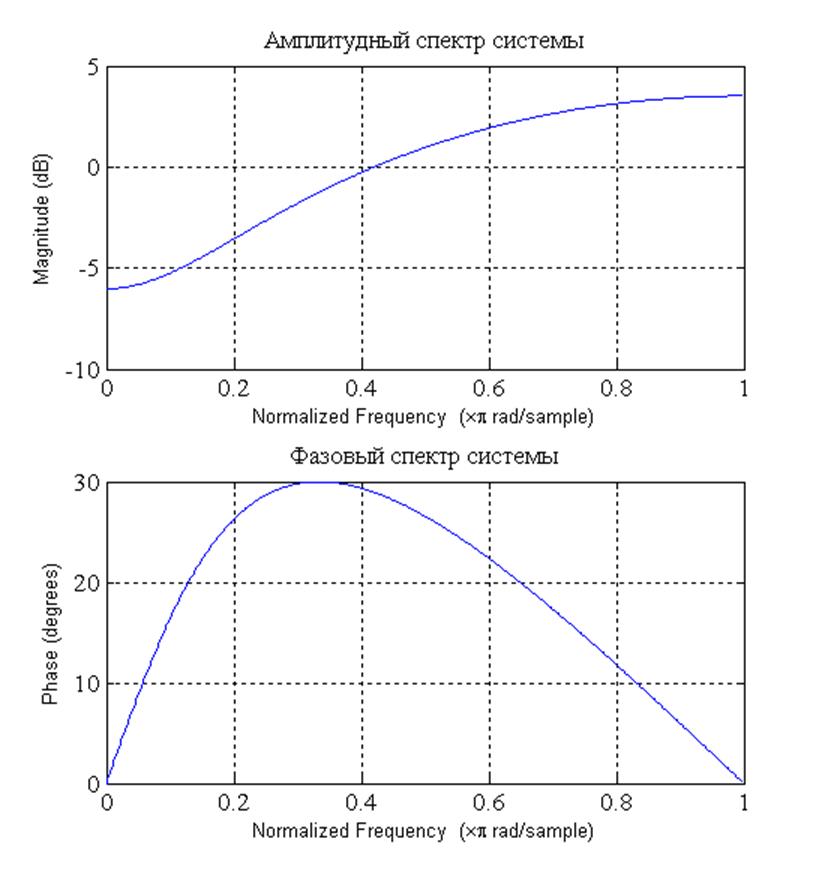
Рис.5. Амплитудный и
фазовый спектры системы с частотной характеристикой 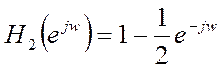
![]() - вычисляет выходной сигнал
- вычисляет выходной сигнал ![]() при прохождении произвольного
входного сигнала
при прохождении произвольного
входного сигнала ![]() через дискретную систему с
передаточной функцией
через дискретную систему с
передаточной функцией ![]() .
.
num = [1];
den = [1,-0.5];
n = 0:20;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.