Информатика и выч. техника \ Теория и обработка сигналов

Z-преобразование и дискретно-временное преобразование Фурье. Вариант 9, страница 3

x = rectpuls(n-10,21);

subplot(3,1,1)

stem(n,x),grid on, axis([-5,25,0,1.5])

set(gca,'FontName','Times New Roman Cyr','FontSize',11), title('Прямоугольный импульс')

set(gca,'FontName','Times New Roman Cyr','FontSize',8),  xlabel('Номер отсчета, N')

X = filter(num,den,x);

subplot(3,1,2)

stem(n,X),grid on, axis([-5,25,0,2.5])

set(gca,'FontName','Times New Roman Cyr','FontSize',11), title('Сигнал на выходе первой системы H1')

set(gca,'FontName','Times New Roman Cyr','FontSize',8),  xlabel('Номер отсчета, N')

Y = filter(den,num,X);

subplot(3,1,3)

stem(n,Y),grid on, axis([-5,25,0,1.5])

set(gca,'FontName','Times New Roman Cyr','FontSize',11), title('Сигнал на выходе второй системы H2')

set(gca,'FontName','Times New Roman Cyr','FontSize',8),   xlabel('Номер отсчета, N')

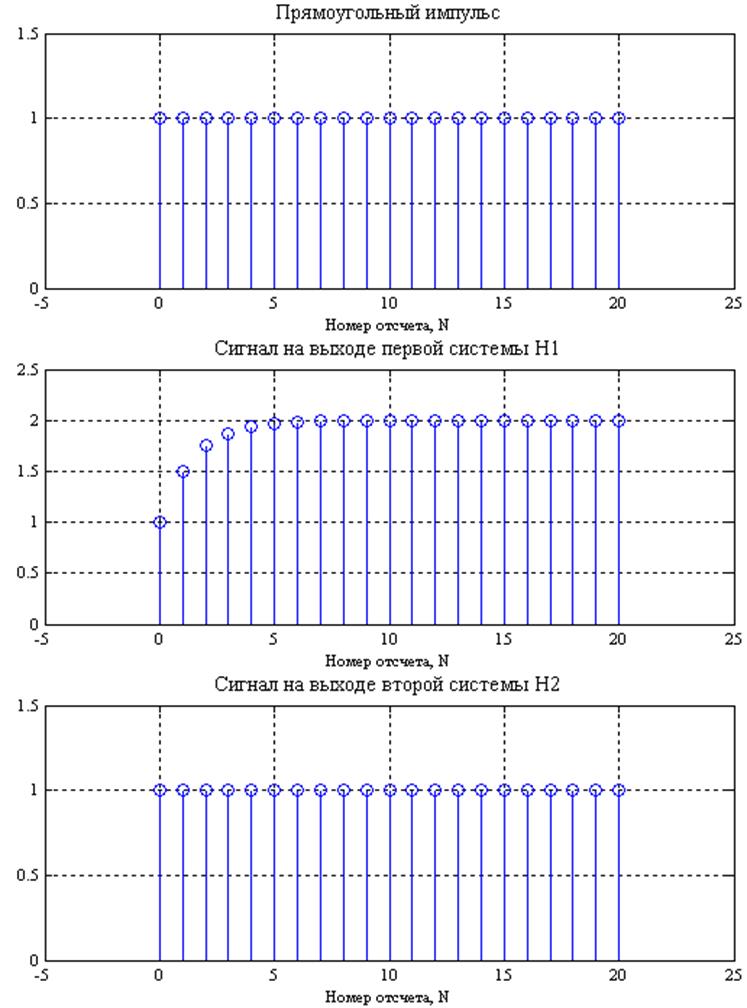
Рис.6. Графики прямоугольного импульса на входе системы ,  сигнала на выходе системы  (на входе системы ) и на выходе системы

Комментарий:       На графиках рис.4 и рис.5 изображены АЧХ и ФЧХ двух систем, каскадное соединение которых имеет частотную характеристику равную единицы. Из графиков видно, что АЧХ и ФЧХ этих двух систем симметричны друг относительно друга. При каскадном соединении двух этих систем, очевидно, что на выходе второй системы будет получен такой же сигнал, как и на входе первой системы. Частотная характеристика – это 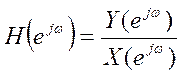, следовательно, если на вход системы подаётся сигнал , имеющий ДВПФ , то на выходе будет сигнал, имеющий ДВПФ , а  этому сигналу во временной области соответствует некий дискретный сигнал , который подаётся на вход второй системы, тогда на выходе каскада будет сигнал, имеющий ДВПФ , но  и, следовательно: . Т.е. на выходе каскада будет то же самое, что и на его входе, что и подтверждается экспериментально: на выходе первой системы - сглаженный в начале прямоугольный сигнал, на выходе второй системы – исходный сигнал.

  1. Обработка звуковых сигналов в среде Matlab.

Для  простоты проведения операций фильтрации была написана программа filterau на языке Matlab’a.

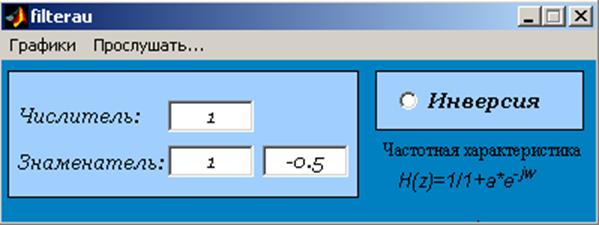
Рис.7 а. Интерфейс программы filterau.

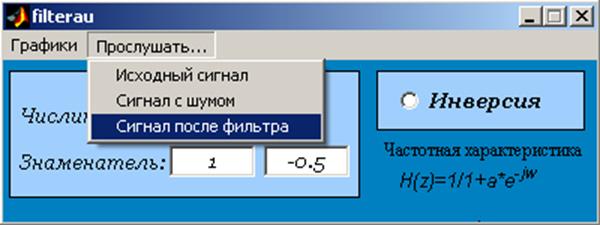
Рис.7 б. Интерфейс программы filterau.

                       

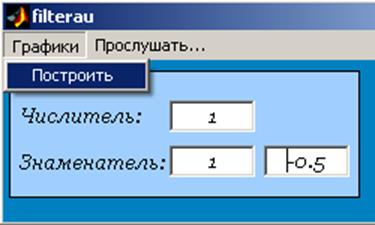
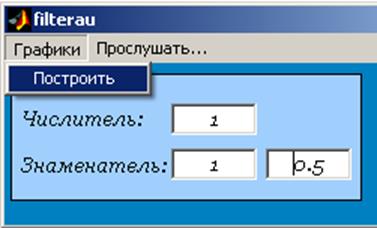
Рис.8. Проведем фильтрацию сигнала фильтром с  частотной характеристико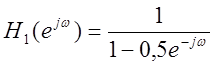й  и .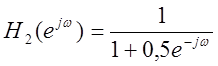

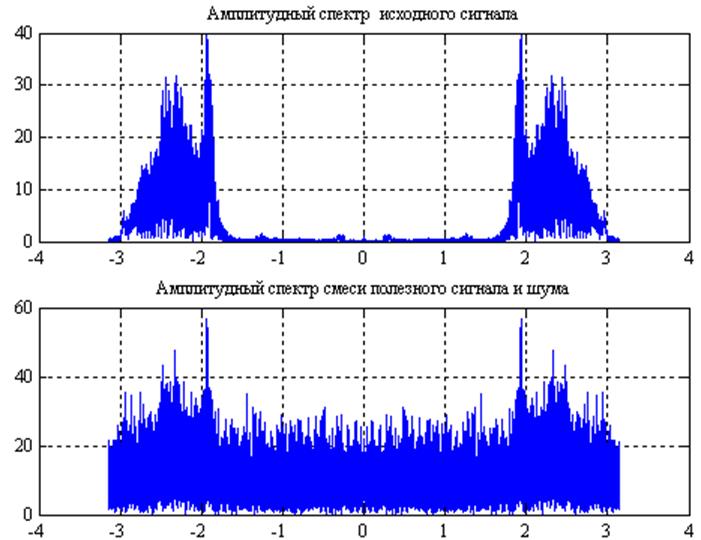
Рис.9. Графики амплитудных спектров исходного сигнала, сигнала с наложением шумов.

             

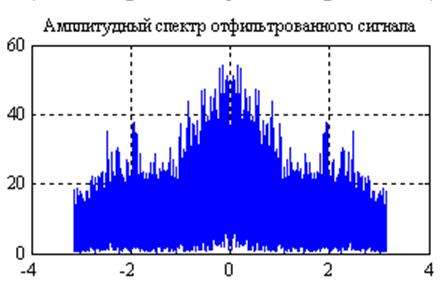
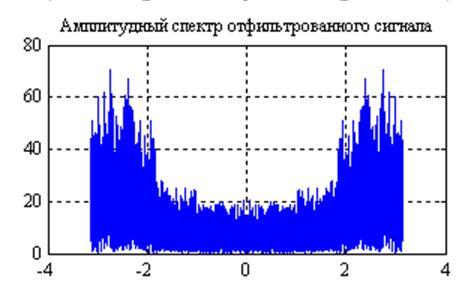
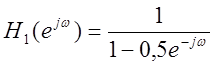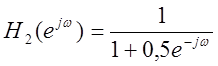Рис.10.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

                    

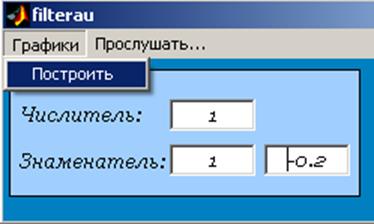
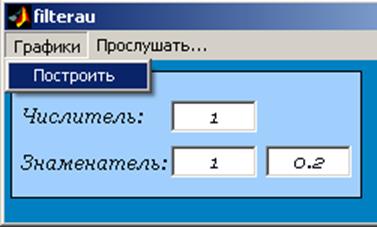
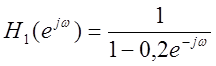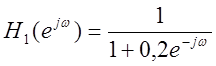Рис.11. Проведем фильтрацию сигнала фильтром с  частотной характеристикой и (слева направо).

                       

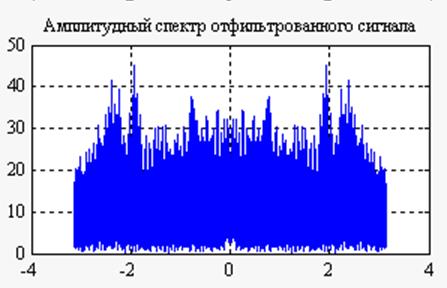
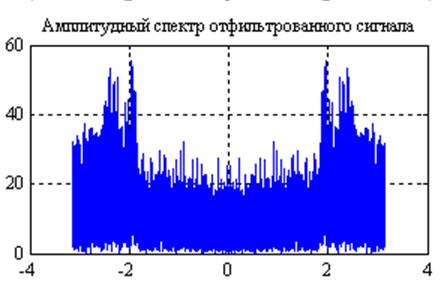
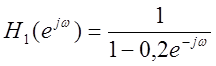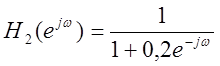Рис.12.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

                 

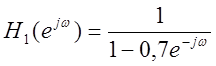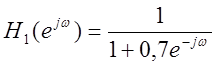Рис.13. Проведем фильтрацию сигнала фильтром с  частотной характеристикой и (слева направо).

           

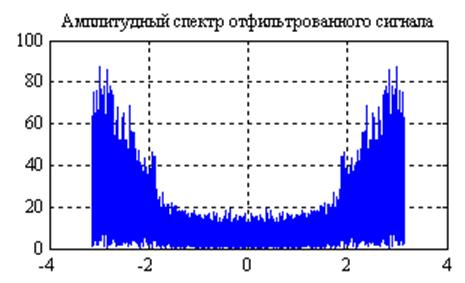
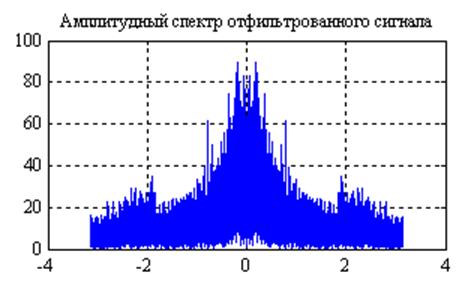
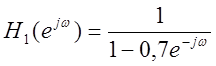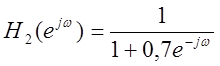Рис.14.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

                   

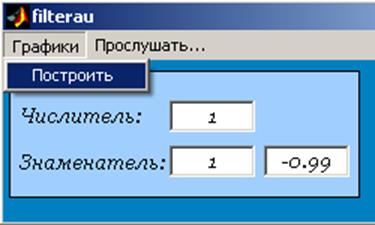
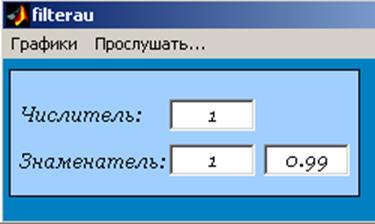
Рис.15. Проведем фильтрацию сигнала фильтром с  частотной характеристико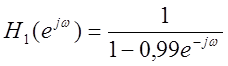й  и .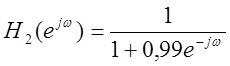

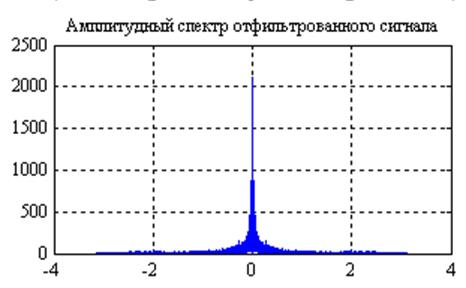
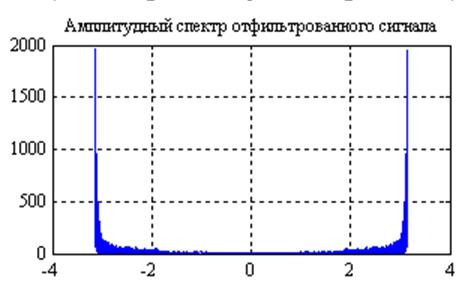
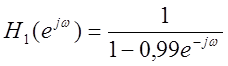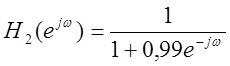Рис.16.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

Комментарий: описание отфильтрованного сигнала приведены в таблице 1:

Таблица 1. Описание отфильтрованного сигнала для соответствующей ЧХ фильтра.

ЧХ фильтра

Описание звукового сигнала, полученного с выхода фильтра

Громкость шума увеличилась, сигнал остался той же мощности.

Полезный сигнал слышен отчетливее, так как фильтр погасил низкочастотные составляющие шума. Все же высокочастотная составляющая шума в сигнале слышна.

Сигнал после фильтра почти не изменился, лишь стал немного глуше.

Как и в случае, когда , сигнал слышен лучше.

Сигнал сильно зашумлен низкочастотным шумом. Звук похож на звук водопада.

Произошло подавление низких частот и усиление высоких, что позволяет слушать полезный сигнал несколько лучше, т.к. сам сигнал высокочастотный.

 

Полезный сигнал практически не слышен, его забивает низкочастотный шелест, переходящий в грохот.

Полезный сигнал так же не слышен. Шум похож на звук аудиторного звонка, высокочастотный.

А теперь будем пропускать смесь сигнала и шума через инвертированный фильтр с ЧХ вида .

Рис.17. Пропустим сигнал через фильтр с инвертированной ЧХ.

                       

Рис.18. Проведем фильтрацию сигнала фильтром с  частотной характеристикой  и .

                   

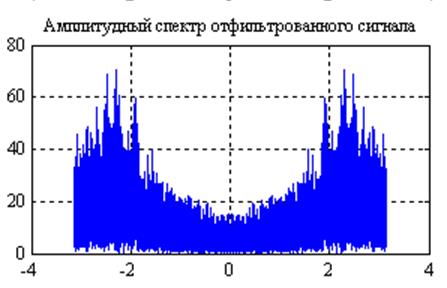
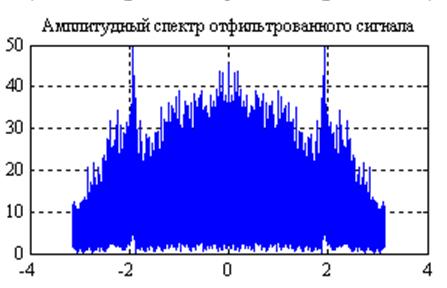
Рис.19.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

                       

Рис.20. Проведем фильтрацию сигнала фильтром с  частотной характеристикой  и .

                          

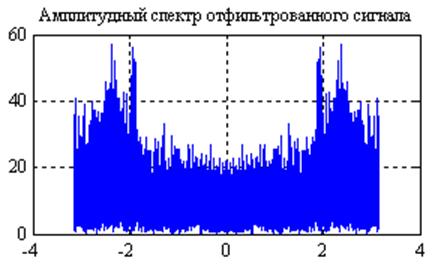
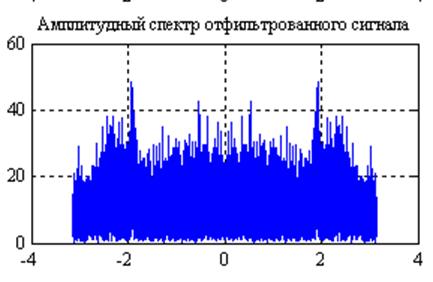
Рис.21.  Графики амплитудных спектров сигнала после прохождения его через фильтр с частотной характеристикой   и (слева направо).

Скачать файл