Рис.22. Проведем
фильтрацию сигнала фильтром с частотной характеристикой 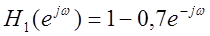 и
и 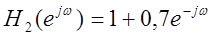 .
.
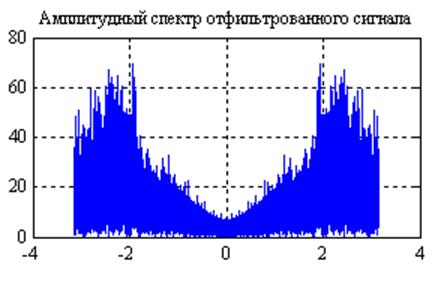
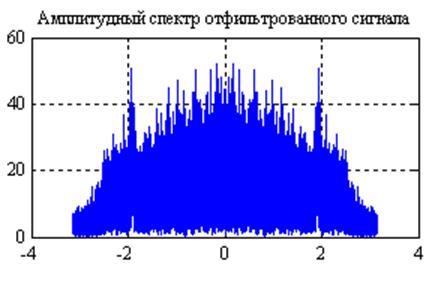
Рис.23. Графики
амплитудных спектров сигнала после прохождения его через фильтр с частотной
характеристикой 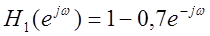 и
и 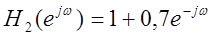 (слева
направо).
(слева
направо).
Рис.24. Проведем
фильтрацию сигнала фильтром с частотной характеристикой 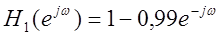 и
и 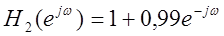 .
.
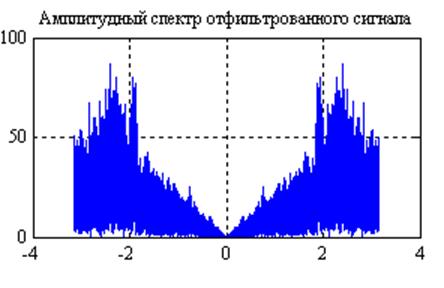
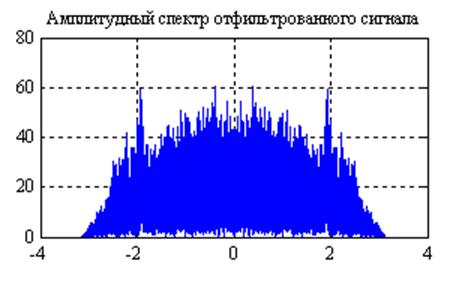
Рис.25. Графики
амплитудных спектров сигнала после прохождения его через фильтр с частотной
характеристикой 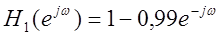 и
и 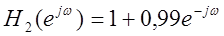 (слева
направо).
(слева
направо).
Комментарий: описание сигнала, отфильтрованного системой
с инвертированной ЧХ, приведены в таблице 2:
Таблица
2. Описание отфильтрованного сигнала для соответствующей ЧХ фильтра.
|
ЧХ фильтра
|
Описание звукового сигнала, полученного
с выхода фильтра
|
|
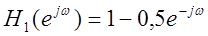
|
Шум приглушен,
полезный сигнал слышен хорошо.
|
|
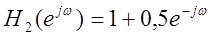
|
Полезный
сигнал слышен плохо, так как фильтр не погасил низкочастотные составляющие
шума, а наоборот, усилил их.
|
|
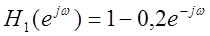
|
Сигнал после
фильтра почти не изменился, лишь стал немного звонче, т.к. низкие частоты
немного погасились.
|
|
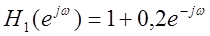
|
Сигналы на
входе и выходе фильтра практически идентичны по звучанию.
|
|
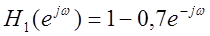
|
Полезный
сигнал на выходе стал вдвое громче, слышен отчетливее. Шум присутствует,
высокочастотный шелест.
|
|
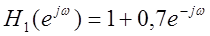
|
Низкие частоты
усилены, сигнал приглушен, почти не слышен.
|
|
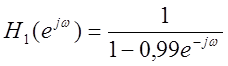
|
Полезный
сигнал слышен хорошо на фоне высокочастотного шума.
|
|
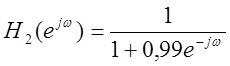
|
Полезный
сигнал заглушен мощной низкочастотной шумовой волной.
|
Вывод по работе: В
данной работе понятия Z-преобразования и ДВПФ приобрели
практический смысл:
- были
произведены непосредственные вычисления Z-преобразований различных сигналов (единичного импульса,
единичной последовательности и дискретного косинуса), в ходе которых стало
ясно, что Z-преобразование необходимо
рассматривать только вместе с его областью сходимости, т.к. в некоторых
случаях, когда сигнал определен для бесконечного числа значений, как,
например, единичная импульсная последовательность, то Z-преобразование для неё может и не
существовать:
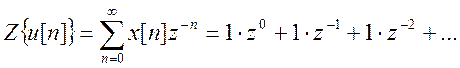 - ряд будет
расходиться при
- ряд будет
расходиться при 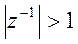 ;
;
- с
помощью средств Matlab, а точнее с помощью функций
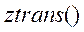 и
и 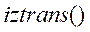 ,
были вычислены прямые и обратные Z-преобразования,
а также полученные результат подтверждены аналитическими расчётами с
использованием свойств Z-преобразования: линейности,
масштабирования, умножения на
,
были вычислены прямые и обратные Z-преобразования,
а также полученные результат подтверждены аналитическими расчётами с
использованием свойств Z-преобразования: линейности,
масштабирования, умножения на 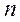 во временной
области и др.;
во временной
области и др.;
- было
вычислено обратное Z-преобразование методом разложения
на простые дроби:
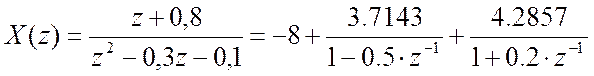 , что позволило на основании табличных преобразований и
свойства запаздывания быстро получить результат:
, что позволило на основании табличных преобразований и
свойства запаздывания быстро получить результат: 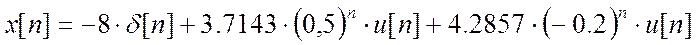 ;
;
- С
помощью Z-преобразования было решено линейное
разностное уравнение:
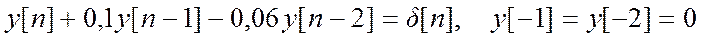 , следуя строго определённому
алгоритму, было получено искомое решение:
, следуя строго определённому
алгоритму, было получено искомое решение:
- взятие
Z-преобразования:
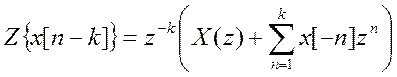 ;
;
- поиск решения
в z-области:
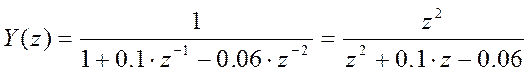 ;
;
вычисление
обратного Z-преобразования: 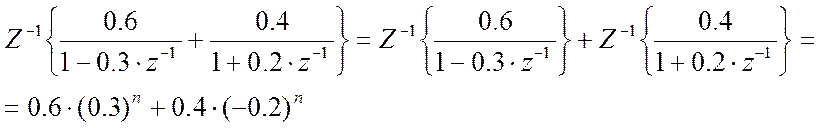
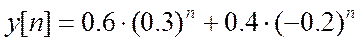 ;
;
- при
непосредственном вычислении ДВПФ дискретного сигнала
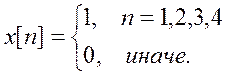 получилось, что ДВПФ – это
ряд Фурье по переменной
получилось, что ДВПФ – это
ряд Фурье по переменной 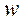 , а
коэффициентами этого ряда являются значения дискретного сигнала:
, а
коэффициентами этого ряда являются значения дискретного сигнала: 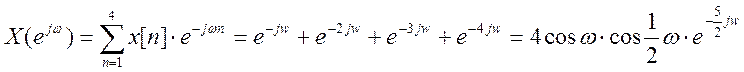 ;
;
- при
вычислении ДВПФ сигнала
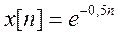 было
показано, что так же, как и для ряда Фурье, с увеличением дискретных
значений сигнала (значений коэффициентов ряда) модуль
было
показано, что так же, как и для ряда Фурье, с увеличением дискретных
значений сигнала (значений коэффициентов ряда) модуль 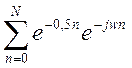 сходиться к модулю предела
сходиться к модулю предела 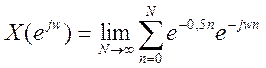 . На рис.1 при
. На рис.1 при 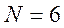 видны колебания в амплитудном
спектре, но уже на рис.2 при увеличении
видны колебания в амплитудном
спектре, но уже на рис.2 при увеличении 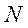 до
до
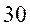 амплитудный спектр сходится к
модулю предела
амплитудный спектр сходится к
модулю предела 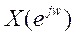 и представляет собой
гладкую линию без пульсаций;
и представляет собой
гладкую линию без пульсаций;
- были
построены АЧХ и ФЧХ двух систем, каскадное соединение которых имеет
частотную характеристику равную единицы. На рис.4 и рис.5. из графиков
видно, что АЧХ и ФЧХ этих двух систем симметричны друг относительно друга.
При каскадном соединении двух этих систем, на выходе второй системы будет
получен такой же сигнал, как и на входе первой системы. Т.е. на выходе
каскада будет то же самое, что и на его входе, что и подтверждается
экспериментально: на выходе первой системы - сглаженный в начале
прямоугольный сигнал, на выходе второй системы – исходный сигнал;
- с
помощью средств Matlab была произведена обработка звуковых
сигналов, а с помощью ДВПФ полученные звуковые сигналы удалось
проанализировать, было выяснено, что при прохождении сигнала с шумами
через фильтр с частотной характеристикой вида
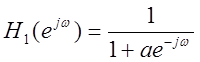 ,
где
,
где 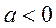 , происходит усиление низких
частот. При прохождении сигнала с шумами через фильтр с частотной
характеристикой вида
, происходит усиление низких
частот. При прохождении сигнала с шумами через фильтр с частотной
характеристикой вида 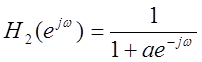 , где
, где 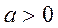 , происходит усиление высоких
частот. Так как в данном случае полезный сигнал был высокочастотным, то в
случае прохождения через фильтры с ЧХ
, происходит усиление высоких
частот. Так как в данном случае полезный сигнал был высокочастотным, то в
случае прохождения через фильтры с ЧХ 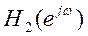 результаты
оказались лучше.
результаты
оказались лучше.
Что касается фильтров с
инвертированными ЧХ, то ситуация противоположная.


![]() и
и ![]() .
.

![]() и
и ![]() (слева
направо).
(слева
направо).

![]() и
и ![]() .
.

![]() и
и ![]() (слева
направо).
(слева
направо).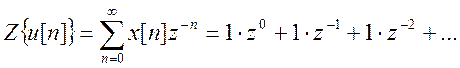 - ряд будет
расходиться при
- ряд будет
расходиться при 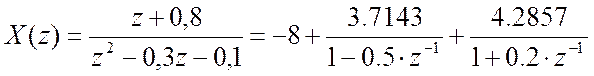 , что позволило на основании табличных преобразований и
свойства запаздывания быстро получить результат:
, что позволило на основании табличных преобразований и
свойства запаздывания быстро получить результат: 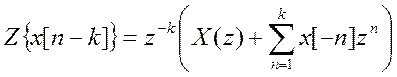 ;
;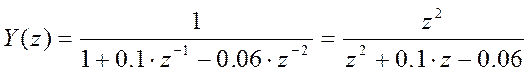 ;
;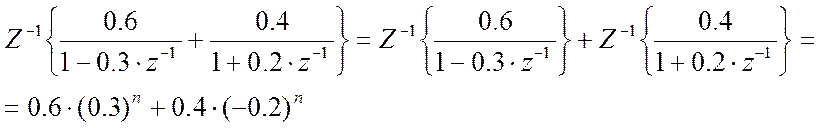
![]() ;
;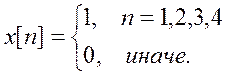 получилось, что ДВПФ – это
ряд Фурье по переменной
получилось, что ДВПФ – это
ряд Фурье по переменной 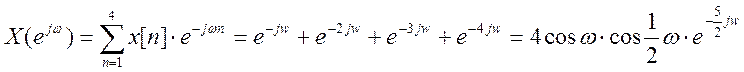 ;
;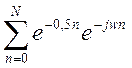 сходиться к модулю предела
сходиться к модулю предела 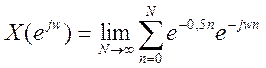 . На рис.1 при
. На рис.1 при 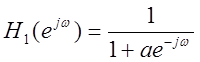 ,
где
,
где 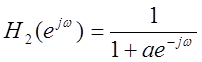 , где
, где