Осуществить преобразование ЧМ-колебания в АМ-колебание можно, используя избирательную систему (в простейшем случае — колебательный контур), к которому прикладывается ЧМ-колебание. На рис. 17.8 приведена схема одноконтурного детектора ЧМ-колебаний, в котором используется этот принцип.
В этом детекторе между базой и эмиттером транзистора VTзадается ЧМ-колебание uЧM(t) = Um соs[ω0t + θ(t)], где Um — амплитуда, θ(t) — мгновенная фаза колебания, а ω0 — частота несущего колебания. Мгновенная фаза колебания θ(t) определяет девиацию частоты Δω(t)=d θ(t)/dt на входе детектора. Для осуществления преобразования ЧМ-колебания в АМ-колебание параметры элементов контура LKи Ск выбирают таким образом, чтобы резонансная частота контура была отлична от частоты ω0 несущего колебания.
На рис. 17.9 приведены диаграммы резонансной характеристики контура, девиации частоты ЧМ-колебания и напряжения на входе АД, поясняющие работу одноконтурного детектора непрерывных ЧМ-колебаний. Анализируя резонансную кривую колебательного контура (см. на рис. 17.9, а), видим, что интенсивность напряжения, падающего на контуре, зависит от частоты. Это используется при преобразовании ЧМ-колебания в АМ-колебание.
Колебательный контур имеет свою резонансную частоту ω0к. Эту частоту выбирают такой, чтобы частота ω0 ЧМ-колебаний располагалась на склоне резонансной характеристики контура. Участок резонансной характеристики в окрестности частоты ω0 должен быть близким к линейному (см. рис. 17.9, а). В этом случае приложение ЧМ-колебания между базой и эмиттером транзистора VT (см. рис. 17.8) вызывает изменение напряжения, падающего на контуре. Так как выбирается линейный участок резонансной характеристики контура, изменения напряжения будут пропорциональны изменениям частоты ЧМ-колебания. В результате этого формируется сигнал с АМ-колебанием (см. рис. 17.9, в). Полученное АМ-колебание поступает на амплитудный детектор. На выходе этого детектора включено ЯС-звено ФНЧ, которое выделит низкочастотную составляющую модулирующего сигнала.
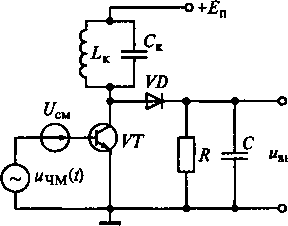
Рис. 17.8. Схема одноконтурного детектора ЧМ-колебаний
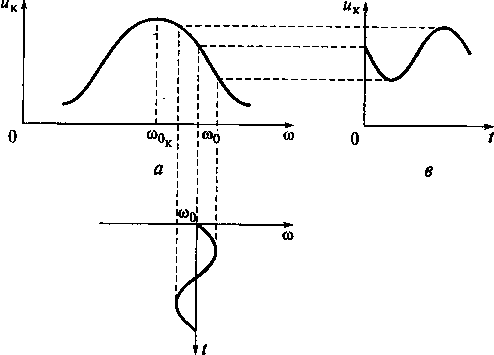
Рис. 17.9. Диаграммы резонансной характеристики контура (а), девиации частоты
ЧМ-колебания (б) и напряжение на входе АД (в)
Недостатком этой схемы является то, что линейный участок резонансной характеристики контура имеет ограниченную протяженность, что приводит к искажению преобразованного АМ-колебания и, соответственно, к искажению сигнала uвых(t) на выходе детектора.
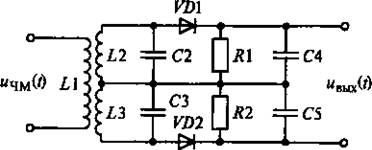
Эти недостатки устраняются в двухконтурном детекторе ЧМ-колебаний, схема которого представлена на рис. 17.10. В этом детекторе контуры, один из которых включает индуктивную катушку L2 и конденсатор С2, а другой — индуктивную катушку Z3 и конденсатор СЗ, имеют свои резонансные частоты ω01 и ω02, отличные от частоты несущего колебания ω0. В результате этого резонансные характеристики контуров оказываются сдвинутыми по оси частот относительно друг друга и относительно частоты ω0 несущего колебания. На рис. 17.11 показаны диаграммы резонансных кривых колебательных контуров, передаточной характеристики детектора, изменения частоты ЧМ-колебания и напряжения на выходе двухконтурного детектора.
![]()
Рис. 17.10. Схема двухконтурного детектора ЧМ-колебаний
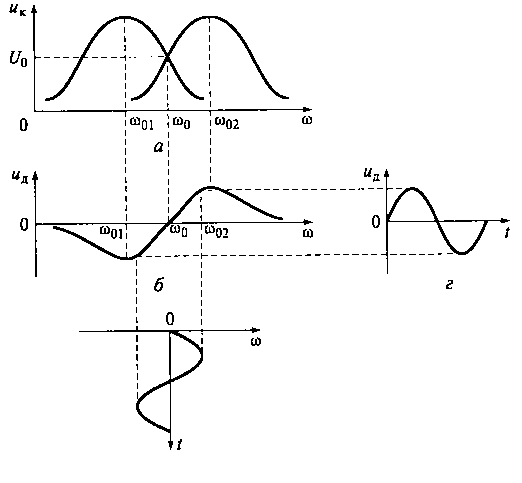
Рис. 17.11. Диафаммы резонансных кривых колебательных контуров (а), передаточной характеристики детектора (б), изменения частоты ЧМ-колебания (в) и напряжения на выходе двухконтурного детектора (г)
Для двухконтурного детектора ЧМ-колебаний передаточную характеристику детектора uд(t)=f(ω) (см. рис. 17.11, б) в пределах линейного участка можно представить в виде uд(t) = Kд(ω - ω0), где Kд = 4Uо/Δω0 — крутизна характеристики детектора,
Δω0 = ω02 - ω01 , a U0— напряжение точки пересечения резонансных кривых контуров. Пусть на детектор с такой передаточной характеристикой подается ЧМ-колебание, частота которого изменяется, например, в соответствии с законом ω = ω0 + Δωcos(Ωt), где Δω — девиация частоты. В этом случае ЧМ-колебание будет преобразовано в АМ-колебание, напряжение которого изменяется пропорционально частоте (см. рис. 17.11, г). В последующем этот сигнал детектируется амплитудным детектором, на выходе которого появляется сигнал, соответствующий модулирующему сигналу.
На рис. 17.12 приведена схема детектора непрерывных ЧМ-колебаний, выполненного на основе аналогового перемножителя.
Работу этого детектора можно рассмотреть, подав на его вход сигнал, изменяющийся по гармоническому закону, u(t) = Umcos(ωt). В этом случае к одному входу умножителя будет приложено напряжение uс(t), падающее на конденсаторе С, а к другому — напряжение, падающее на контуре, uk(t). Ток источника входного напряжения будет протекать через конденсатор С и контур. При этом, так как ток емкости опережает входное напряжение на угол π/2, то ее напряжение можно представить в виде uc(t) = Uccos(ωt - π/2).
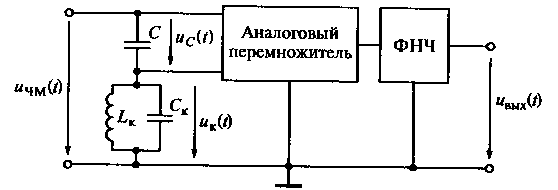
Рис. 17.12. Схема детектора непрерывных ЧМ-колебаний на основе
аналогового перемножителя
Напряжение, падающее на контуре, uk(t) = Ukcos(ωt+φ), где φ = -arctg(2QΔω/ω0) — фазовый сдвиг между током и напряжением контура; QK-добротность контура;
Δω= ω - ω0— абсолютная расстройка между текущей ω и резонансной частотой контура ω0. Тогда напряжение на выходе перемножителя можно представить в виде
uумн(t) = kuс(t)uк(t) = kUcUk cos(ωt - π/2)cos(ω t+ φ) =
= 0,5kUcUkcos(φ + π/2) + 0,5kUcUkcos(2ωt + φ - π/2).
Спектральная составляющая, изменяющаяся с удвоенной частотой 2ω, будет подавлена ФНЧ, в результате чего на выходе детектора будет присутствовать только низкочастотная составляющая uвых(t) = 0,5kUcUkcos(φ + π/2) = -0,5kUcUksin(φ).
Так как в параллельном колебательном контуре, как правило, выполняется условие 2QΔω/ ω0 « 1, то можно принять, что sinφ= 2QΔω/ω0, откуда имеем uвых(t)=-kUcUkQkΔω/ω0.Из этого выражения видим, что детекторы ЧМ-колебаний, построенные на аналоговых перемножителях, являются линейными. Однако аналоговые перемножители имеют относительно низкие рабочие частоты, что не всегда позволяет построить детекторы непрерывных ЧМ-колебаний на их основе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.