На рис. 16.6 приведена структурная схема амплитудного модулятора с одной боковой полосой, а на рис. 16.7 представлены диаграммы спектра амплитуд АМ-колебания, модуля коэффициента передачи напряжения
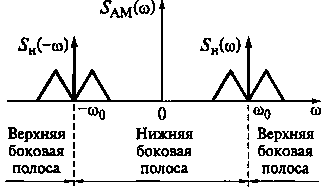
Рис. 16.5. Спектр АМ-колебаний
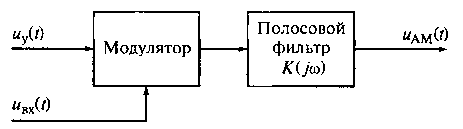
Рис. 16.6. Структурная схема амплитудного модулятора с одной боковой полосой
ПФ и спектра амплитуд АМ-колебания с одной боковой полосой, поясняющие работу амплитудного модулятора, в котором выделяется нижняя боковая полоса. Такой модулятор обеспечивает получение АМ-колебания с подавлением либо без подавления спектральной составляющей несущего колебания (см. рис. 16.7, а).
Полосовой фильтр (ПФ) с коэффициентом передачи K(ω) (см. рис. 16.7, б) выделяет нижнюю или верхнюю боковые полосы спектра АМ-колебания (см. рис. 16.7, в). На рис. 16.7, в видно, что ширина спектра SОБП(ω) АМ-колебания с одной боковой полосой равна максимальной частоте спектра Qmax управляющего сигнала. Это позволяет, например, в сравнении с обычным АМ-колебанием, в 2 раза увеличить число каналов связи в заданном диапазоне частот (16.1).
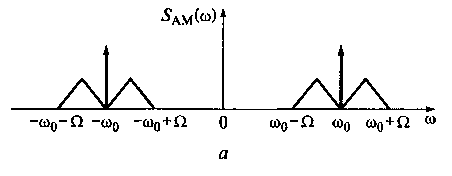
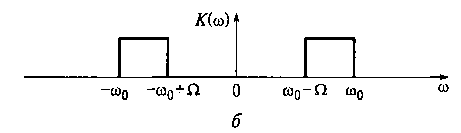
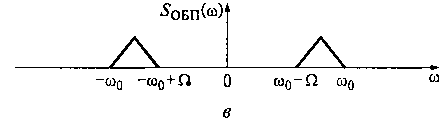
Рис 16.7. Спектр амплитуд АМ-колебания (а), модуль коэффициента
передачи напряжения ПФ (б) и спектр амплитуд АМ-колебания с ОБП
одной боковой полосой (в)
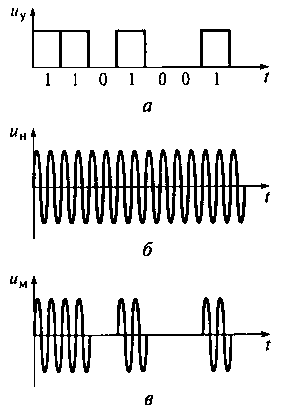
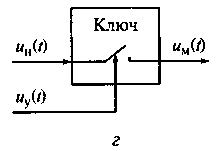
Рис. 16.8. Последовательность двоичных символов (а), несущее колебание (б), последовательность радиоимпульсов амплитудно-манипулированного колебания (в) и структурная схема амплитудно-манипулированного модулятора (г)
Недостатком модуляторов, формирующих модулированные колебания с одной боковой полосой, является необходимость использования сложных ПФ, которые должны обеспечивать высокую прямоугольность частотной характеристики.
На рис. 16.8 показаны последовательность двоичных символов, несущее колебание, последовательность радиоимпульсов амплитудно-манипулированного колебания и структурная схема амплитудно-манипулированного модулятора. Для передачи данных, представленных потоком двоичных символов (0,1) (см. рис. 16.8, а), в цифровом канале связи используют амплитудно-манипулированную модуляцию. Роль амплитудно-манипулированного модулятора (см. рис. 16.8, г) выполняет электронный ключ, на один вход которого поступает несущее колебание uн(t) = Umнcos(ω 0t), представляющее собой гармоническую функцию (см. рис. 16.8, б).
При поступлении на управляющий вход модулятора двоичного сигнала, характеризующего логический нуль (низкий уровень управляющего сигнала), ключ размыкается и на выход модулятора несущее колебание не проходит, а при поступлении на управляющий вход модулятора двоичного сигнала, характеризующего логическую единицу (высокий уровень управляющего сигнала), ключ замыкается и на выход модулятора проходит сигнал несущего колебания (см. рис. 16.8, в). Выходной сигнал uм(t) амплитудно-манипулированного модулятора будет представлять собой последовательность радиоимпульсов (см. рис. 16.8, в). Длительность огибающей радиоимпульса равна длительности одного или нескольких, следующих друг за другом импульсов, соответствующих логической единице кодового слова управляющего сигнала. Амплитуда огибающей радиоимпульса соответствует амплитуде несущего колебания.
16.2. Формирование ЧМ-колебаний
Формирование ЧМ-колебаний базируется в основном на использовании радиокомпонентов (конденсаторы, индуктивные катушки), параметры (емкость, индуктивность) которых изменяются в соответствии с изменением интенсивности управляющего сигнала. Подобными радиокомпонентами могут быть, например, полупроводниковые диоды в обратном включении, варикапы, p-n-переход база— коллектор биполярных транзисторов. Эти радиокомпоненты включают в колебательный контур. Зависимость параметров радиокомпонентов от управляющего (модулирующего) сигнала uy(t) приводит к тому, что и резонансная частота колебательного контура будет зависеть от этого же сигнала.
Допустим, имеется колебательный контур, состоящий из индуктивной катушки и конденсатора, емкость которого изменяется по закону
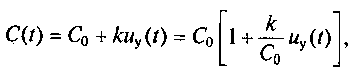
где k — постоянный коэффициент с размерностью Ф/В.
Резонансная частота этого колебательного контура
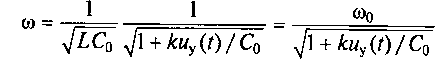
где ω 0 = 1/√(LC0) — резонансная частота контура в исходной рабочей точке нелинейного конденсатора С = С0 при uy(t) = 0.
Если выполняется условие kuy(t)/C0 « 1, то справедливо приближение
ω = ω 0+βuу(t), (16.3)
где β = -0,5k/С0 — коэффициент частотной модуляции.
На рис. 16.9 приведена схема модулятора ЧМ-колебаний. В этой схеме генератор гармонических колебаний выполнен на транзисторе VT1. Резисторы R4 и R5, задавая напряжение смещения U6 =ЕпR5/(R4+R5) на базу транзистора, определяют положение рабочей точки, относительно которой формируется колебательный процесс. Резисторы R1 и R2 определяют величину начальной емкости С0 варикапа VD1 при uу(t) = 0, задавая напряжение смещения Uвар = EnR2/(R1 + R2).Колебательный контур состоит из индуктивной катушки L2, конденсаторов С2 и С4 и емкости варикапа VD1. Он включен в коллекторную цепь транзистора. Конденсатор СЗ выступает в роли элемента, обеспечивающего положительную обратную связь в генераторе гармонических колебаний. Он передает часть сигнала с коллектора транзистора к эмиттеру. При правильном выборе величины емкости
+еп
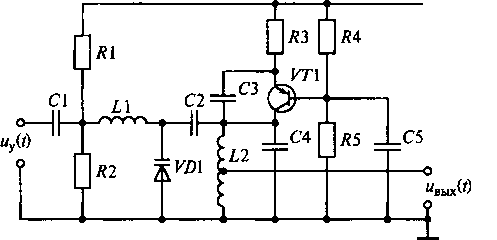
Рис. 16.9. Схема модулятора ЧМ-колебаний
конденсатора СЗ в генераторе обеспечивается незатухающий колебательный процесс. Варикап выполняет роль конденсатора переменной емкости. При изменении управляющего напряжения uy(t)относительно рабочей точки, определяемой напряжением Uвар, изменяется и емкость варикапа VD1 и, соответственно, происходит изменение частоты генератора (16.4). В результате этого формируется ЧМ-колебание.
Конденсатор С1 разделяет источник управляющего напряжения и варикап по постоянному току. Индуктивная катушка L1 исключает шунтирование варикапа низким выходным сопротивлением источника управляющего напряжения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.