Из последнего слагаемого полученного выражения имеем
iФМ (t) = 0,5 a2UmUon sin[φ(t)]+ 0,5 a2UmUon sin[2ω0t + φ(t)].
Спектральные составляющие, описываемые последним слагаемым этого выражения, могут быть легко подавлены ФНЧ (RC-звено). Соответственно, на выходе детектора появится низкочастотная составляющая сигнала, зависящая от значения фазы сигнала uвых(t) = 0,5a2UmUonRsin[φ(t)].
При малом коэффициенте фазовой модуляции можно принять, что sin[φ(t)]≈φ(t). С учетом этого напряжение на выходе детектора принимает вид uвых(t) = 0,5a2UmU0ПRφ(t).
Таким образом, выходное напряжение детектора ФМ-колебаний пропорционально фазе входного напряжения при малом коэффициенте фазовой модуляции.
Детектор ФМ-колебаний можно построить, используя аналоговый перемножитель. В этом случае диапазон изменения фазы сигнала расширяется, однако при использовании аналоговых перемножителей детектирование возможно только в диапазоне относительно низких частот.
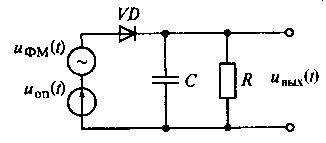
Рис. 17.17. Схема перемножителя сигналов на основе полупроводникового диода
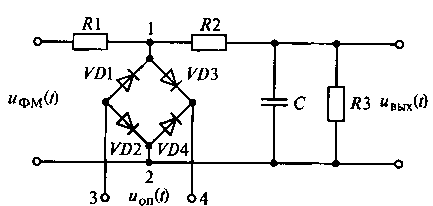
Рис. 17.18. Схема перемножителя сигналов с использованием электронного ключа
на основе диодного моста
В области высоких частот детектирование ФМ-колебаний в широким диапазоном изменения фазы сигнала возможно при использовании в качестве перемножителя сигналов различного рода электронных ключей. В качестве электронного ключа можно использовать транзисторы или диодный мост. Схема перемножителя сигналов с использованием электронного ключа на основе диодного моста показана на рис. 17.18.
В этом детекторе опорное напряжение uоп(t) = cos(ω0t), а ФМ-колебание можно описать выражением uфм(t) = Umcos[ω0t + φ(t)]. Когда между узлами 3 и 4 действует положительная полуволна опорного напряжения, диоды VD2 и VDЗ проводят токи. Сопротивление резистора R1 существенно больше сопротивления диода в открытом состоянии. В этом случае протеканием токов через резисторы R1 и R2 можно пренебречь, а потенциалы узлов 1 и 2 можно считать одинаковыми. Это соответствует замкнутому состоянию ключа, когда ФМ-колебание на выход детектора не проходит.
Если между узлами 3 и 4 действует отрицательная полуволна опорного напряжения, то токи через диоды VD2 и VD3 не протекают, ключ находится в разомкнутом состоянии, соответственно, на выходе детектора действует ФМ-колебание.
Так как ФМ-колебание и опорное напряжение отличаются фазой φ(t) сигнала, зависящей от времени, то среди множества спектральных составляющих, присутствующих на зажимах 1 и 2 ключа, будут присутствовать и спектральные составляющие, зависящие только от фазы сигнала. Высокочастотные составляющие спектра будут подавлены ФНЧ (резистор R3 и конденсатор С), а на выходе детектора будет выделяться низкочастотная составляющая сигнала uвых(t) = - (Um /π)sin[φ(t)].
Линейность передаточной характеристики детекторов с использованием электронного ключа несколько выше, чем детекторов, построенных на одном диоде, однако не всегда достаточна. Использование в качестве опорного напряжения и ФМ-колебания сигналов типа меандр позволяет повысить линейность характеристики детектора и, соответственно, расширить диапазон изменения фазы сигнала.
ГЛАВА 18
ПАРАМЕТРИЧЕСКИЕ ЦЕПИ
18.1. Понятие и характеристики параметрической цепи
Под параметрическими цепями понимают цепи, состоящие из множества радиоэлементов (элементов), при этом параметры одного или нескольких из них изменяются во времени при приложении к цепи электрических колебаний. Элемент, хотя бы один параметр которого изменяется во времени, называется параметрическим.
В цепях в качестве параметрических элементов могут выступать параметрические сопротивления R(t), емкости С(t) или индуктивности L(t).«Параметричность» этих элементов заключается в том, что основные (сопротивление, емкость или индуктивность) или производные (крутизна, величина заряда) их параметры изменяются во времени.
Для рассмотрения вопроса по формированию параметрических элементов на рис. 18.1 приведена диаграмма проходной ВАХ iк = f/(uбэ) биполярного транзистора. Вольт-амперная характеристика этого резистивного элемента носит явно выраженный нелинейный характер, а его сопротивления (статическое и дифференциальное) зависят от напряжения, приложенного к нему. Статическое сопротивление определяется при медленно меняющихся сигналах, поэтому оно от времени не зависит, а дифференциальное сопротивление Rдиф = du/diопределяется при быстро изменяющихся сигналах и, соответственно, зависит от приращений напряжения на этом нелинейном резисторе и тока, протекающего через него.
На практике при рассмотрении параметрических цепей чаще пользуются не понятием «дифференциальное сопротивление», а понятием «дифференциальная крутизна». Этот параметр является обратной величиной сопротивлению. В нашем случае дифференциальная крутизна определяется выражением S = di/du.
Дифференциальная крутизна характеризует изменение тока, протекающего через нелинейный резистор при приложении к нему переменного напряжения.
Допустим, для нелинейного резистора, ВАХ которого приведена на рис. 18.1, определено положение исходной рабочей точки (Uo, Iо). Относительно напряжения смещения U0приложено управляющее напряжение, которое изменяется по гармоническому закону uy(t) = Uycos (ω0t). В пределах изменения управляющего напряжения uy(t)ВАХ нелинейного резистора можно аппроксимировать (описать) полиномом второй степени
i =a0(U0) +a1(иу -U0)+ а2(иу- U0)2, где a0(U0) = I0 — ток нелинейного резистора в
рабочей точке.
Осуществив дифференцирование, найдем выражение для описания поведения дифференциальной крутизны нелинейного резистора в окрестности рабочей точки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.