Частотная модуляция может осуществляться как относительно непрерывных управляющих сигналов, так и относительно дискретных сигналов. При дискретной модуляции (манипуляции) частота несущего колебания изменяется дискретно в соответствии с кодом дискретного управляющего сигнала. Основание кода может быть различным, но наиболее часто используются двоичные коды, когда, например, высокий уровень сигнала отражает логическую единицу, а низкий — логический нуль.
Структурная схема модулятора дискретного ЧМ-колебания приведена на рис. 16.10, а на рис. 16.11 показаны диаграммы управляющего двоичного сигнала, сигнала инверсного к нему, не-
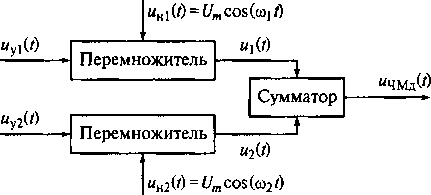
Рис. 16.10. Структурная схема модулятора дискретного ЧМ-колебания
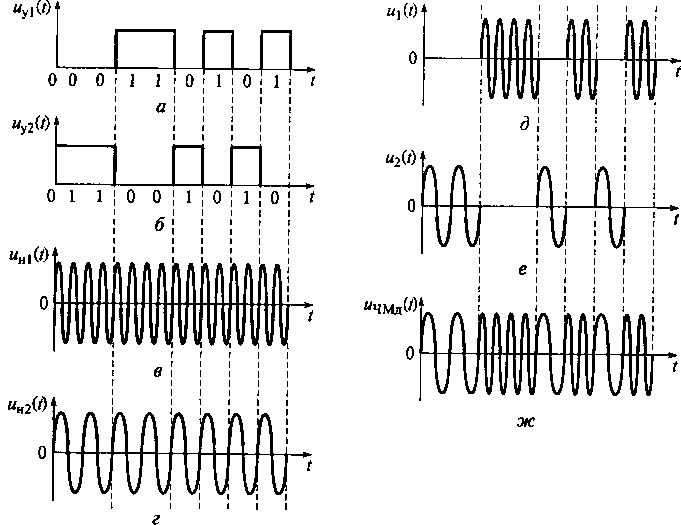
Рис. 16.11. Диаграммы управляющего двоичного сигнал а (а) и сигнала инверсного к нему (б), первого (в) и второго (г) несущих колебаний, сигналов на выходах первого (д) и второго (е) перемножителей дискретного ЧМ-колебания (ж)
сущих колебаний сигналов на выходах перемножителей и дискретного ЧМ-колебания. Модулятор включает два перемножителя дискретных сигналов uу1(t) (см. рис. 16.11, а) и uy2(t) (см. рис. 16.11, б) на сигналы несущих колебаний uн1 = Umcos(ω 1t) (см. рис. 16.11, в) и uн2(t) = Umcos(ω 2t) (см. рис. 16.11, г), изменяющиеся соответственно с частотами ω 1 и
ω 2. Дискретный сигнал uy2(t) инверсен к сигналу uy1(t). Действительно, если значение сигнала uyl(t) равно логической единице, то значение сигнала uy2(t) равно логическому нулю, и наоборот.
На выходе перемножителей, в роли которых могут выступать электронные ключи (см. рис. 16.8, г), появляются сигналы u1(t) = uyl(t)Umcos(ω 1t) (см. рис. 16.11, д) и u2(t) = =uy2(t)Umcos(ω 2t) (см. рис. 16.11, е), представляющие собой радиоимпульсы.
Сигналы с выходов перемножителей поступают на входы сумматора, на выходе которого формируется дискретный ЧМ-сигнал (см. рис. 16.11, ж):uЧМд(t) = u1(t) + u2(t)= uyl(t)Umcos(ω1t) + uy2(t)Umcos(ω2t), представляющий собой последовательность радиоимпульсов, изменяющихся с частотой ω1 или ω 2.
16.3. Модуляторы ФМ-колебаний
Для формирования непрерывных ФМ-колебаний можно использовать модулятор, схема которого представлена на рис. 16.12. Имеется несущее колебание uнс(t) = =Umcos(ω 0t), изменяющееся по косинусоидальному закону, и управляющий сигнал uy(t). Несущее колебание одновременно поступает на фазовращатель, который обеспечивает сдвиг фазы несущего колебания на 90°, и балансный модулятор. На выходе фазовращателя сигнал несущего колебания изменяется по закону синуса uнс(t) =Umsin(ω 0t). На выходе балансного модулятора формируется АМ-колебание uAM(t)= mAMuy(t)cos(ω 0t) с подавленной несущей. Сигналы с выходов фазовращателя и балансного модулятора поступают на сумматор. На выходе сумматора формируется ФМ-колебание, которое может быть описано выражением
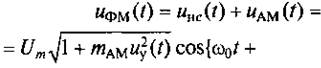
arctg[mAMuy(t)]}.
Такой способ формирования ФМ-колебаний имеет существенный недостаток: его можно использовать только при малом коэффициенте фазовой модуляции mфм= kUy« 1.
С учетом этого непрерывные ФМ колебания можно формировать на относительно низкой частоте. Для перехода в требуемый диапазон частот необходимо производить многократное умножение частоты. Это, как правило, существенно усложняет исходную схему формирования ФМ-колебаний.
Существуют и другие способы формирования непрерывных ФМ-колебаний. Однако ранее отмечалось, что ширина спектра таких колебаний не остается постоянной и зависит от частоты управляющего сигнала, поэтому непрерывные ФМ-колебания не находят широкого применения.
Широкое применение находят модуляторы дискретных ФМ-колебаний. Дискретный сигнал можно представить как в виде многоуровневого сигнала, так и в виде последовательности двоичных символов. Под многоуровневым дискретным сигналом пони-
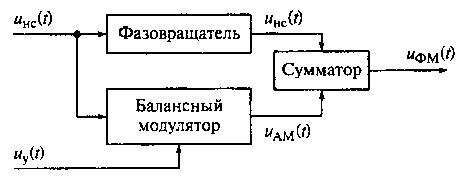
Рис. 16.12. Схема модулятора непрерывных ФМ-колебаний
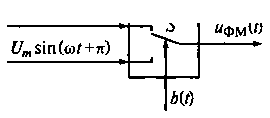
Рис. 16.13. Структурная схема двоичного фазового модулятора
мают сигнал, для которого каждый уровень может быть описан конкретным числом. Под двоичными символами понимают последовательность логических единиц или нулей, когда в одном разряде (в пределах одного единичного интервала) кодового слова может присутствовать логическая единица или нуль в зависимости от состояния сигнала. Последовательность двоичного сигнала имеет вид 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, ... .
Как многоуровневые сигналы, так и последовательность двоичных символов можно представить в виде 2mкодовых комбинаций, где т — число уровней сигнала или число двоичных символов в двоичной последовательности. В любом из этих случаев каждая из 2m комбинаций может быть задана радиоимпульсом, в котором гармонический сигнал имеет свою начальную фазу.
Многоуровневые сигналы не находят широкого применения в цифровых устройствах из-за сложности их формирования и обработки. Однако последовательности двоичных символов в пределах одного единичного интервала являются частным случаем многоуровневых сигналов, когда число уровней равно двум. Кроме того, последовательности двоичных символов могут быть использованы для описания более сложных многоуровневых сигналов, когда каждому уровню сигнала присваивается своя точно известная последовательность двоичных символов. В этом случае можно рассматривать m-кратную фазовую модуляцию. Каждой кратности ФМ-сигнала соответствует свой набор фаз гармонического колебания в дискретном сообщении. Например, при т = 1, что соответствует одному единичному интервалу последовательности двоичных символов, число начальных фаз отрезков гармонических функций равно двум, при т = 2 число начальных фаз 22 = 4, при т = 4 число начальных фаз 24= 16 и т.д.
Для примера на рис. 16.13 приведена структурная схема двоичного фазового модулятора с числом начальных фаз равным двум, а на рис. 16.14 приведены диаграммы управляющего двоичного сигнала, несущих колебаний и дискретного ФМ-колебания, поясняющие работу этого модулятора. На входы двоичного фазового модулятора поступают два несущих колебания uн1(t) = Um sin(ωt) (см. рис. 16.14, б) и uн2(t) = Um sin(ωt+π) (см. рис. 16.14, в). Частоты этих несущих колебаний совпадают, а начальные фазы различны. Например, начальная фаза первого несущего колебания равна нулю градусов, а второго π.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.