S[uy(t)] = а1 + 2a2uy(t), где а1= s0— крутизна нелинейного резистора в исходной рабочей точке. Из этого выражения видно, что если ВАХ нелинейного резистора в окрестности исходной рабочей точки может быть аппроксимирован полиномом второй степени, то дифференциальная крутизна в окрестности этой точки будет изменяться по линейному закону (см. рис. 18.1). При этом, так как управляющее напряжение uy(t)= Uycos(ωyt) зависит от времени, то и дифференциальную крутизну можно рассматривать зависимой от времени. Таким образом, относительно дифференциальной крутизны S(t), зависящей от времени, нелинейный резистор может рассматриваться как параметрический элемент.
Дифференциальная крутизна S(t) может быть как положительной, так и отрицательной. Если с ростом управляющего напряжения uуотносительно исходной рабочей точки растет и ток (точка 1 на рис. 18.1), то дифференциальная крутизна S(t) будет положительной. Если с ростом управляющего напряжения uу относительно исходной рабочей точки происходит снижение тока (точка 4 на рис. 18.1), то в этом случае дифференциальная крутизна S(t) будет отрицательной.
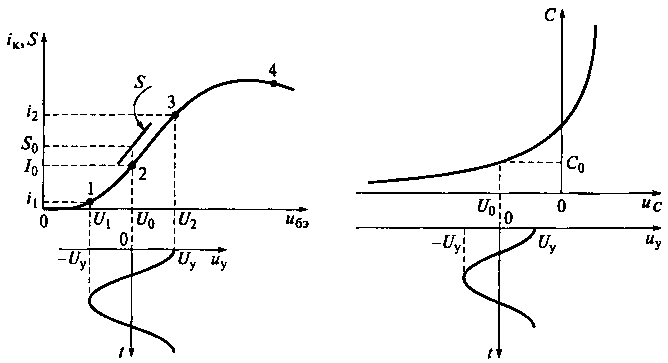
Рис. 18.1. Диаграмма проходной ВАХ Рис. 18.2. Диаграмма зависимости барьерной
ik =f( uбэ) биполярного транзистора емкости p-n-перехода БТ от напряжения,
приложенного к нему
Рассмотрим зависимость заряда, накапливаемого в нелинейной емкости, от напряжения. На рис. 18.2 показана диаграмма зависимости барьерной емкости p-n-перехода БТ от напряжения, приложенного к нему.
В окрестности исходной рабочей точки изменение заряда qнелинейной емкости можно аппроксимировать полиномом второй степени q=q0 + b1 (u-U0) + b2(u - U0)2,
где q0 — заряд емкости в исходной рабочей точке нелинейной емкости.
Пусть к нелинейной емкости приложено напряжение, изменяющееся по гармоническому закону uу= Uycos(ωyt). Тогда изменение дифференциальной емкости описывается формулой
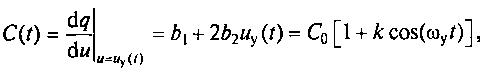
где b1 = C0— величина емкости в исходной рабочей точке u=U0; k=2b2Uy/C0— глубина изменения емкости.
Таким образом, при приложении к нелинейной емкости переменного напряжения ее дифференциальная емкость будет зависеть от изменения этого напряжения и, соответственно, может рассматриваться как емкость, зависящая от времени, так как управляющее напряжение зависит от времени. С учетом этого нелинейная емкость может быть использована в качестве параметрического элемента, дифференциальная емкость C(t) которого зависит от времени.
Обобщая результаты, полученные при анализе дифференциальной крутизны S(t) нелинейного резистора и дифференциальной емкости C(t) p-n-перехода, отметим следующее. Параметрический элемент — это совокупность одного из нелинейных элементов (сопротивление, емкость или индуктивность) и источника управляющего напряжения, напряжение которого изменяется, например, по гармоническому закону относительно исходной рабочей точки нелинейного элемента. На рис. 18.3 показана структурная схема представления параметрического элемента.
Используя параметрические элементы, можно строить различные радиотехнические устройства, в частности, малошумящие параметрические усилители, модуляторы и преобразователи частоты, генераторы и детекторы.
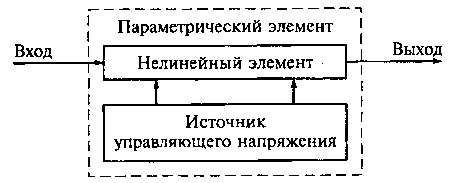
Рис. 18.3. Структурная схема представления параметрического элемента
18.2. Прохождение сигналов через линейные параметрические цепи
При рассмотрении линейных радиотехнических цепей с постоянными параметрами отмечалось, что отклик цепи при известном входном воздействии можно определить различными способами. Наиболее часто при анализе цепей в частотной области используют передаточную характеристику цепи K(jω). Если задана спектральная плотность сигнала на входе цепи Sвх(jω), то спектральная плотность сигнала на выходе цепи может быть рассчитана по формуле Sвых(jω) = Sвх(jω)K(jω). При анализе цепи во временной области пользуются интегралом Дюамеля и импульсной характеристикой h(τ) цепи. Тогда
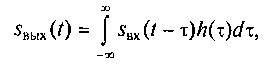
где Sвх(t) и Sвых(t) — сигналы на входе и выходе цепи соответственно.
Однако в параметрических цепях передаточная характеристика зависит как от частоты ω, так и от времени t, в соответствии с которым изменяются параметры нелинейного элемента и цепи в целом. В этом случае передаточная характеристика цепи принимает вид K(jω,t). Импульсная характеристика параметрической цепи также зависит от нескольких параметров: с одной стороны, от интервала времени t-τ, определяющего, момент приложения единичного импульса и момент времени наблюдения отклика сигнала, а с другой стороны, от расположения момента времени t-τ на временной оси. В этом случае импульсная характеристика параметрической цепи принимает вид h(t,τ).
Зависимость передаточной K(jω,t) и импульсной h(t, τ) характеристик параметрической цепи от двух параметров усложняет вычислительный процесс при анализе радиотехнических устройств, поэтому решение таких задач возможно при учете определенных допущений, например, в электрической цепи какой-либо параметр изменяется по периодическому закону.
При изменении передаточной характеристики цепи по сложному, но периодическому закону с частотой Ω на выходе цепи образуется спектр сигнала, содержащий составляющие с частотами ω±Ω; ω± 2Ω и т.д., где ω - частота входного сигнала.
В линейной параметрической цепи никакого взаимодействия между спектральными составляющими не происходит, т.е. выходной сигнал не содержит спектральных составляющих с комбинационными частотами nω1 ± mω2, где ω и ω2 — частоты спектральных составляющих входного сигнала.
Проанализируем работу устройств на базе параметрических элементов.
18.3. Параметрическое усиление сигналов
Для построения параметрических усилителей используют нелинейные энергоемкие элементы (емкости и индуктивности). Усиление сигналов основано на том, что амплитуда сигнального напряжение Ucсущественно меньше амплитуды управляющего Uу. В этом случае сигнальное напряжение ис не оказывает влияния на изменение, например, дифференциальной емкости нелинейного конденсатора. При этом изменение величины дифференциальной емкости (уменьшение) под действием управляющего напряжения иу в параметрическом элементе не приводит к изменению заряда, накопленного в емкости. В то же время это способствует увеличению сигнального напряжения на емкости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.