Математическая среда связи характеристик надежности с критерием потенциальной эффективности электронных средств (Квалификационная работа бакалавра), страница 9

     В практике разработки ЭС важное значение имеет точность технологических процессов создания ЭС. Замечаем, что выражения (2.6, 2.7, 2.8) не отвечают данному требованию. Для более объективного решения рассматриваемой задачи необходимо, чтобы выражения (2.6, 2.7, 2.8) отражали возможности технологических процессов создания ЭС. С этой целью вводится коэффициент технологической изменчивости. Он записывается так

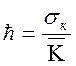                                                               .                                                   (2.9)

    Из выражения (2.9) очевидно, что меньшей величине соответствуют более современные технологические процессы. Для глубокоёмких и высокоточных технологических процессов создания  новейших ЭС данный коэффициент (2.9) находится в пределах .

     Для введённого коэффициента  следует показать функциональную зависимость

                                                , при  .                                (2.10)

Из предыдущих расчётов имеем, что среднеквадратическое отклонение критерия качества соответственно для рабочего и всех участков функции качества находится в приделах

.

При этом средние значения критерия качества соответственно для этих участков равны

,                        .

Результаты расчетов сведены в таблицу 2.2.

                                                                                                            Таблица 2.2

Зависимость коэффициента технологической изменчивости от среднеквадратического отклонения критерия ПЭ

№	Средние величины критерия ПЭ
	Рабочий участок		Весь участок
1	0,0665	0,0563	0,0815	0,0563
2	0,0725	0,0613	0,0887	0,0613
3	0,0784	0,0663	0,0959	0, 0663
4	0,0843	0,0713	0,1032	0,0713
5	0,0902	0,0763	0,1104	0,0763
6	0,0961	0,0813	0,1176	0,0813
7	0,1020	0,0863	0,1249	0,0863
8	0,1079	0,0913	0,1321	0,0913
9	0,1138	0,0963	0,1394	0,0963
10	0,1197	0,1013	0,1466	0,1013

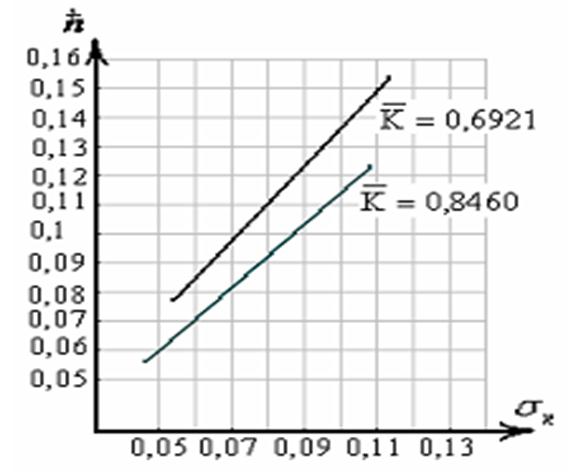
              Рис.2.7. Зависимость критерия технологической изменчивости от                среднеквадратического отклонения критерия ПЭ

Графическая зависимость функции (2.9) показана на рис.2.7 , который имеет линейный вид. Из рис.2.7 очевидно, что меньшей величине соответствует больший коэффициент технологической изменчивости. Это объясняется тем, что обеспечить высокую точность технологических процессов создания ЭС в более широком диапазоне функции качества существенно сложнее. Чем для рабочего её участка.

     Затем формируется вероятностные модели связи характеристик надёжности с      критерием ПЭ ЭС.

Р а с п р е д е л е н и е   в е р о я т н о с т и   д о с т и г н у т о г о   у р о в н я   к р и т е р и я   П Э   Э С

Для построения математической модели вероятности достигнутого уровня ПЭ ЭС при их разработке воспользуемся аргументом функции Лапласа. Для этой функции делаем не сложные преобразования, затем, учитывая коэффициент технологической изменчивости, получаем

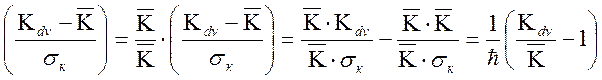               .                                                                 (2.11)

Тогда на основе выражений (2.6) не трудно записать вероятность достигнутого уровня критерия ПЭ ЭС с учётом  технологической изменчивости

                                 

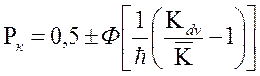
                                 (2.12)

где обратная величина коэффициента технологической изменчивости.

     С позиции технологических процессов разработки ЭС величина  соответствует коэффициенту не обратимых изменений.

     П л о т н о с т и   р а с п р е д е л е н и я   д о с т и г н у т о г о   у р о в н я  

к р и т е р и я   П Э   ЭС

     Для построения математической модели плотности распределения достигнутого уровня критерия ПЭ, воспользуемся выражением (2.7). В практике использование вероятностных характеристик удобнее использовать выражение (2,7) в нормальном виде

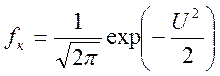                                              .                                    (2.13)           

Тогда, используя выражения (2.9, 2.10) не трудно получить плотность распределения достигнутого уровня критерия ПЭ ЭС.

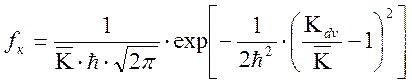                                 .                     (2.14)

В нормированном виде выражение  (2.14)  записывается так

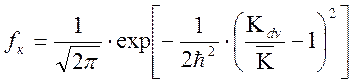                                   .                        (2.15)

 Р а с п р е д е л е н и е   о п а с н о с т и   о т к а з о в   д о с т и г н у т о г о        

у р о в н я   к р и т е р и я   П Э   Э С

Для построения математической модели опасности отказов достигнутого уровня критерия ПЭ ЭС воспользуемся выражением

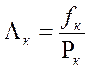
                                            (2.16)

Характерно, что выражение (16) справедливо для любого закона распределения случайных величин. Из анализа теоретических исследований известно, что опасность распределения соответствует дифференциальному закону.   

Тогда выражение (2.16) перепишется в виде

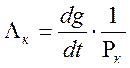                                                                                         (2.17)

Из практических соображений считается, что в процессе разработки ЭС необходимо достигать высокой их надёжности, исходя из технологического уровня данного производства. Поэтому справедливо полагать, что в оптимальном случае величина  должна  достигать единице. Тогда выражение (2.17) записывается 

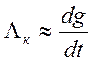                                                                                                 (2.18)

В процессе разработки ЭС происходит формирование значений  их параметров. Однако на достижение требуемых  их величин влияет множество факторов. В частности к ним можно отнести следующие:

 неточность производственных процессов;

 меры по защите  от внешних и внутренних дестабилизирующих факторов;

 возможности конструкций по обеспечению требуемой работоспособности ЭС  и др.