Математическая среда связи характеристик надежности с критерием потенциальной эффективности электронных средств (Квалификационная работа бакалавра), страница 6

Свойства ЭС не несут в себе количественной основы. Отражением свойств являются параметры, которые несут количественную характеристику изделия. Главная сложность заключается в выборе и обосновании множества параметров, наиболее полно характеризующих всё качество устройства. Если рассмотреть наиболее распространенные параметры – надёжность, вес, габариты, стоимость, то для различного назначения и условий эксплуатации в каждом конкретном случае один из этих критериев является наиболее важным. В частности для бортового ЭС наиболее весомых будет надёжность, затем вес и менее значимым стоимость. Для космической ЭС  вес оказывается более значимым критерием, чем объём. Более того, даже на различных стадиях разработки и производства ЭС одного назначения и условий эксплуатаций важность критериев часто изменяется. Например, на начальных этапах создания ЭС с крайне малым весом устройства, важным параметром является его вес. На этапе разработки опытного образца на первое место выступает надежность. И, наконец, при разработки серийного образца определяющим является стоимость. В настоящее время существуют различные подходы для обоснования выбора множества параметров при оценки качества разрабатываемого ЭС.

По аналогии со свойствами, качество ЭС также имеет иерархическую структуру. Управляющей характеристикой является комплексный критерий качества разрабатываемого устройства. По задорному множеству значений параметров технического задания определяется величина этого критерия. На каждом из этапов создания ЭС проводятся испытания: первое–  на этапе проектирования, второе – на этапе изготовления, третье – на этапе эксплуатации. Результатом испытаний является оценка каждого из множества параметров: проектирования Х_п, изготовления Х_и, эксплуатации Х_э. По этим множествам параметров рассчитывается комплексные критерии  качества: К_п, К_и, К_э. Сравнение каждого из них с заданным значением обеспечивается цепями обратной связи. При этом вырабатываются управляющие воздействия на каждом этапе испытаний ЭС:

;  ,

где К_i – значение комплексного критерия качества после i-го вида испытаний.

По результатам корректировки принимается решение о возможности передачи объекта на следующую позицию технического процесса. Если , то обратная связь замыкается для каждого этапа создания ЭС. Для аппаратуры с недостаточным уровнем качества принимаются меры, предусматривающие доработку надёжных узлов в соответствии с замечаниями

проводимых испытаний, корректировку технической документации. Если не удается добиться      на данном уровне конструкторско- технологических возможностей производства, то по согласованию с заказчиком можно изменить техническое задание.

Значит, оценка качества ЭС на каждом этапе их создание необходима для обеспечения процесса его управления с целью достижения требуемого его уровня. Однако для этого необходима математическая модель. В данной работе рассматривается возможность оценки качества ЭС на основе аддитивной и мультипликативной моделей комплексного критерия.

Для оценки достигнутого уровня качества ЭС необходимо использовать все параметры, которыми оно характеризуется: функциональные, электрические, конструкторско- технологические, надежности, экономические и т.д. Большему множеству параметров ЭС будет соответствовать более объективная оценка уровня его качества. Предварительно множество параметров, которыми характеризуется ЭС, разбиваются на условные группы. К первой группе относятся параметры, которые имеют нижний допустимый предел. Например, надёжность радиоприёмного устройства. Такие параметры характеризуются тем, что с увеличением их значений качество ЭС улучшается. Ко второй группе параметров относятся такие, которые имеют верхний допустимый предел, такие параметры характеризуются тем, что с уменьшением их значений качество ЭС улучшается. Например, чувствительность радиоприемного устройства.

Известно, что параметры ЭС имеют различные единицы измерения. Для дальнейших расчётов они являются не сопоставимыми. Поэтому параметры ЭС приводят к безразмерному виду, что обеспечивает их сопоставимость. Для параметров первой группы используются соотношения:

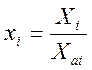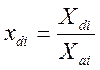                                 ; ; ,                                          (2.1)

где Х_i, X_di, X_ai  – соответственно номинальное допустимое и базовое значение i- го параметра. Для параметров второй группы используются соотношения:

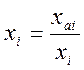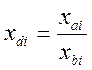                                           ; ; ,                                          (2.2)

Параметры с двухсторонними допусками приводятся к одному из соотношений (2.1), (2.2) в зависимости от того, в какую область допустимых пределов попадает величина параметра.

Практически базовые значения параметров ЭС отражают уровень, с которым сравнивается достигнутое качество ЭС при его разработке в этом множестве параметров. Базовый образец должен быть аналогичен оцениваемому ЭС: по назначению, условиям эксплуатации, видам параметров. В качестве базовых образцов часто используют величины параметров технического создания.

Аддитивная и мультипликативная модели оценки уровня количественной составляющей качества ЭС имеют вид:

                                   

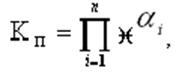
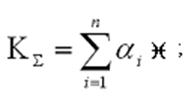
где , – соответственно критерии качества на основе аддитивной и мультипликативной моделей; i_i– оценка i-го параметра модели; – весовой коэффициент оценки  i-го параметра; n – количество параметров.

Математические модели аддитивная и мультипликативная не имеют существенных преимуществ по отношению друг к другу. Поэтому практически используется одна из них. Однако аддитивную модель целесообразно использовать тогда, когда достигнутые значения параметров достаточно близки к их базовым величинам. В остальных случаях целесообразно использовать мультипликативную модель, которая даёт наилучшее сглаживание.

Выражения (2.1), (2.2) отражают линейную зависимость между параметрами и из безмерными значениями. Такая зависимость справедлива для малых отклонений номинальных значений параметров от их базовых величин. Однако, указанные отклонения могут достигать существенных величин. Известно, что чем лучше значение параметра, тем дальше оно отстоит от допустимой величины. При этом дальнейшее улучшение параметра связано как с техническими, так и с экономическими трудностями, что приводит к уменьшению  скорости роста параметра.