Это ведёт к отклонению величин параметров от их номинальных значений, что в свою очередь приводит к появлению погрешности критерия ПЭ. Исходя из сказанного выражение (2.18) представляется в виде
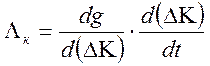 .
(2.19)
.
(2.19)
Далее в выражение (2.19) вводится вариация погрешностей
процесса разработки. Тогда имеем ![]()
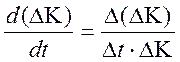 (2.20)
(2.20)
где ![]() значение времени, которое
можно выбрать из ряда (100, 200, 500, 1000)ч.;
значение времени, которое
можно выбрать из ряда (100, 200, 500, 1000)ч.;![]() –
вариация погрешностей.
–
вариация погрешностей.
Заметим, что при определении интенсивности отказов элементов экспериментальным путём, время испытаний чаще всего берут равным 1000 ч. Далее исходим из трёх среднеквадратических отклонений в интервале вариаций.
![]() (2.21)
(2.21)
Следует полагать, что коэффициент технологической изменчивости и величины погрешностей, связанная с вариацией практически будет совпадать. Это связано с одинаковыми конструктивно- технологическими возможностями производственного процесса при создании ЭС.
Тогда на основе отмеченных положений и используя выражения (2.14, 2.19, 2.20, 2.21) получаем опасность отказов достигнутого уровня критерия ПЭ ЭС.
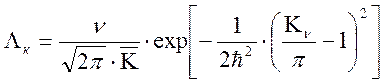 (2.22)
(2.22)
Если ![]() является
нормированной величиной, то имеем
является
нормированной величиной, то имеем
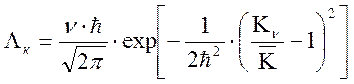 (2.23)
(2.23)
Где ![]() – величина зависящая от
временного ряда. Она рассчитывается по формуле
– величина зависящая от
временного ряда. Она рассчитывается по формуле
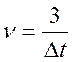 (2.24)
(2.24)
Таким образом, в результате проведённых расчётов получены вероятностные характеристики в математической связи их с критерием ПЭ с учётом коэффициента технологической изменчивости.
Р а с п р е д е л е н и е с р е д н е г о в р е м е н и б е з о т к а з н о й
р а б о т ы о т д о с т и г н у т о г о у р о в н я к р и т е р и я П Э
Для вывода математической модели также распределения воспользуемся выражением (2.7)
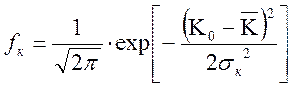
(2.25)
Над выражением (2.25) делаются следующие преобразования
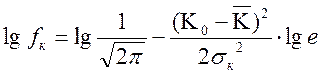
(2.26)
Подставляя значения логарифмов, получаем
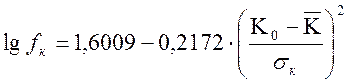 (2.27)
(2.27)
Дальнейшие преобразования приводят к следующему выражению
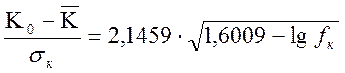 (2.28)
(2.28)
Характерно, что при разработке ЭС наиболее важным является достижение
высокого уровня надёжности тогда выражение (2.28) перепишется в виде
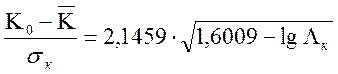 (2.29)
(2.29)
Далее вводится функция нормированного времени
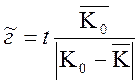
![]() (2.30)
(2.30)
где ![]() – значение реального
времени.
– значение реального
времени.
Для дальнейших преобразований в выражение (2.30)
необходимо ввести среднее время безотказной работы вместо величины текущего
времени ![]() .
.
Тогда функция (2.30) перепишется в виде
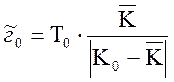 (2.31)
(2.31)
где ![]() – среднее время безотказной
работы в нормированном виде.
– среднее время безотказной
работы в нормированном виде.
Выражение (2.31) приводим к следующему виду
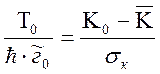 (2.32)
(2.32)
Результатом сравнения двух выражений (2.29, 2.32) является математическая модель связи среднего времени безотказной работы ЭС с опасностью отказов,
![]() (2.33)
(2.33)
Следует заметить, что в свою очередь опасность отказов функционально связана с критерием ПЭ. Значит перед опасностью отказов среднее время безотказной работы связано с достигнутым уровнем критерия ПЭ на этапе разработки ЭС. Выражение (2.33) отражает накапливаемый технический потенциал при разработке ЭС в виде среднего времени безотказной работы. При этом характерно, что с данным показателем надёжность в дальнейшем ЭС выйдет на этап постоянной эксплуатации. Это важное положение позволяет функцию (2.33) записать в следующем виде
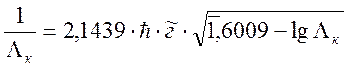 (2.34)
(2.34)
Анализ выражения (2.34) показал, что в нём можно выделить следующий фрагмент его структуры
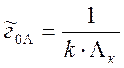 (2.35)
(2.35)
где k– количественная
составляющая выражения (2.34); где ![]() – нормированное
среднее время выраженное через опасность отказов и количественной составляющей.
Практические расчёты показывают, что величина k для рабочего участка функции качества находится в пределах
– нормированное
среднее время выраженное через опасность отказов и количественной составляющей.
Практические расчёты показывают, что величина k для рабочего участка функции качества находится в пределах ![]() = (0,5869 – 0,733).
= (0,5869 – 0,733).
В целом математические модели (2.28, 2.35) позволяют связать среднее время безотказной работы со способностью отказов ЭС в процессе его разработки.
3 Практическая реализация методики
3.1 Функция количественной связи достигнутого уровня критерия ПЭ ЭС с вероятностью его достижения
Для построения графической зависимости данного распределения используется математическая модель:
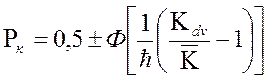
При этом основными исходными данными для расчётов соответственно для рабочего и всего участков функции является следующее:
![]() среднее
значения функции качества
среднее
значения функции качества
![]() ;
; ![]() ,
,
![]() среднеквадратические
отклонения критерия
среднеквадратические
отклонения критерия
![]() ;
; ![]() ,
,
![]() коэффициенты
технологической изменчивости
коэффициенты
технологической изменчивости
![]() ;
;
![]() .
.
Результаты расчётов сведены в таблицы
3.1 и 3.2 соответственно для рабочего и для всего участка функции, графические
зависимости ![]() представлены на рис. 3.1 и 3.2. При
этом не трудно построить графическую зависимость вероятности достигнутого
уровня критерия ПЭ от аргумента функции Лапласа. При этом характерно, что такая
зависимость по своей форме полностью повторяет функцию
представлены на рис. 3.1 и 3.2. При
этом не трудно построить графическую зависимость вероятности достигнутого
уровня критерия ПЭ от аргумента функции Лапласа. При этом характерно, что такая
зависимость по своей форме полностью повторяет функцию
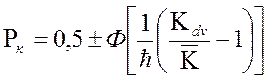 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.