Математическая среда связи характеристик надежности с критерием потенциальной эффективности электронных средств (Квалификационная работа бакалавра), страница 7

Значит, изменение оценки параметра происходит на монотонно возрастающей функции.

С учётом сказанного, оценку параметра и её допустимую величину определяют по выражениям

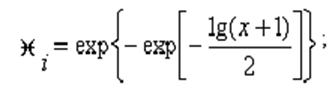
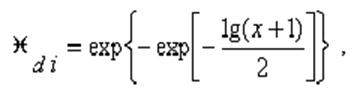
где  i_di – оценка допустимого значения i-го параметра.

Оценка параметра изменяется в интервале

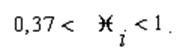
Если х_i =0, то i_i =0,37. Если х_i 0, то i_i 0. При достижении номинального значения параметра базовой величины оценка параметра  i_i равна 0,692.

Весовые коэффициенты оценок параметров отражают степень их влияния на критерий качества ЭС. При этом изменение параметров в допустимых пределах приводит к изменению степени их влияния на критерий качества ЭС. Поэтому весовые коэффициенты оценок параметров определяют на основе информации, содержащейся между номинальными и допустимыми значениями параметров. Соответственно для аддитивной и мультипликативной моделей выражения весовых коэффициентов имеют вид:

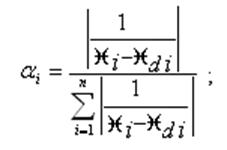
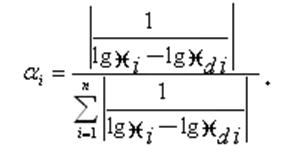
Использовав выражения (2.3), (2.4), (2.5) нетрудно оценить достигнутый уровень качества ЭС на соответствующем этапе его создания. При этом возможно следующее. Если К_{∑ , П} > 0,692, то достигнутое качество ЭС выше уровня базового образца. Если К_{∑ , П} < 0,692, то достигнутое качество ниже уровня базового образца. Если базовые значения параметров отражают требования технического задания, то достигнутый уровень качества ЭС будет соответствовать требованиям технического задания, либо не соответствовать им.

Затем рассчитывается погрешность оценки качества ЭС. Вначале определяется оценка дисперсии критерия качества по формуле

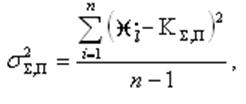
Тогда абсолютная и относительная погрешность критерия качества ЭС равны:

          

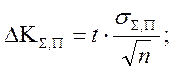
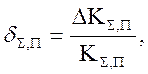
Где  — среднеквадратическое отклонение критерия качества; t— критерий Стьюдента. 

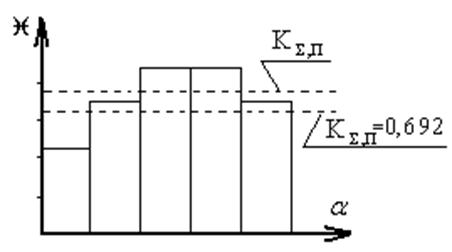
                                       Рис 2.1. Диаграмма качества ЭС

Анализировать достигнутый уровень качества ЭС удобно по диаграмме его качества. На основе аддитивной модели она строится, как показано на рис. 2.1. На оси абсцисс откладываются весовые коэффициенты оценок параметров в пропорциональном масштабе, когда конец одной величины служит началом другой.

 На оси ординат откладываются оценки параметров. Прямоугольники,
которые по высоте ниже уровня 0,692 отражают качество ЭС ниже базового
образца. Широкие прямоугольники имеют большую величину весовых коэффициентов оценок параметров. Очевидно, что сумма площадей прямоугольников отражает величину критерия качества ЭС. На основе мультипликативной модели диаграмма качества строится аналогично. Предварительно её выражение (3) приводится к виду:

 

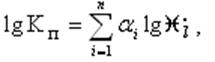
вводится замена, в результате получаем

         

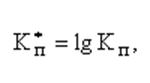
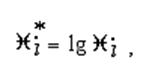
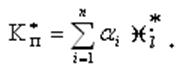
Поскольку оценки параметров являются показателями качества, то их логарифмы также будут показателями качества.

 

2.2 Математическое моделирование закона нормального 

распределения

  При решении задач оценки и управления ПЭ ЭС важно знать законы распределения   параметров   на   этапах   и   стадиях   их   разработки.   В

литературе обширно и глубоко рассматриваются различные законы распределения случайных величин.

Известно, что к случайным величинам относятся как значения параметров, так и величины их допусков. Однако отсутствуют конкретные рекомендации о соответствующем законе распределения того или иного параметра ЭС.

Заметим, что в пределах заданного допуска величины параметра распределяются случайным образом, то соответствие его распределения конкретному закону должно проводиться по правилам теории вероятностей. На рис.2.2 показано равномерное распределение плотности вероятности параметра .

Рис.2.2. Равномерное распределение плотности вероятности

Пусть имеется композиция двух параметров с равномерным их распределением. В результате суммирования двух случайных величин данного распределения с одинаковыми областями рассеивания получаем закон распределения равнобедренного треугольника (рис.2.3).

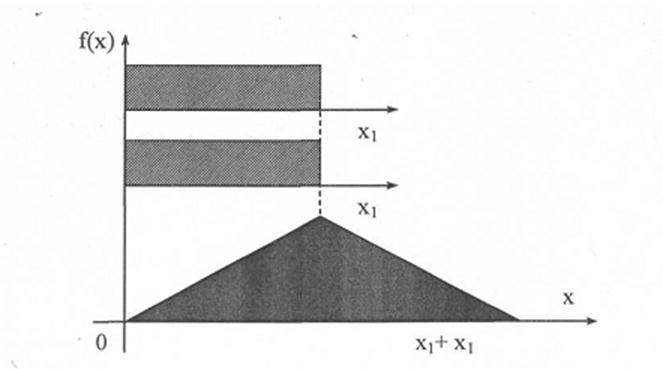
Рис.2.3. Распределение плотности вероятности по закону треугольника

Если же области рассеивания двух случайных величин различны при равномерном законе их распределения, то суммирование их приводит к трапециидальной форме закона. При этом, чем больше разность областей рассеивания, тем длиннее верхняя линия трапеции (рис.2.4).

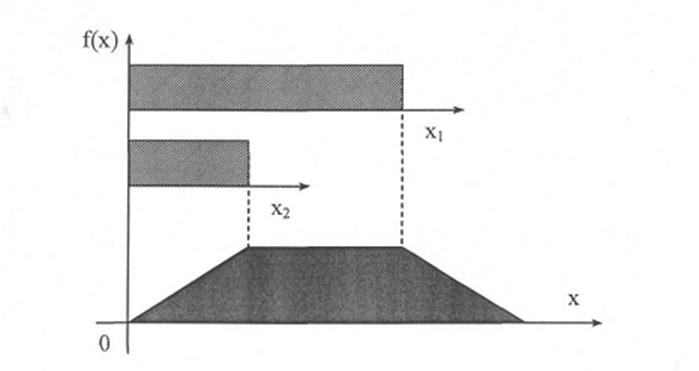
Рис.2.4. Распределение плотности вероятности по закону трапеции

     Характерно, что композиция двух случайных величин, подчиняющихся закону равнобедренного треугольника, соответствует нормальному закону (рис.2.5).

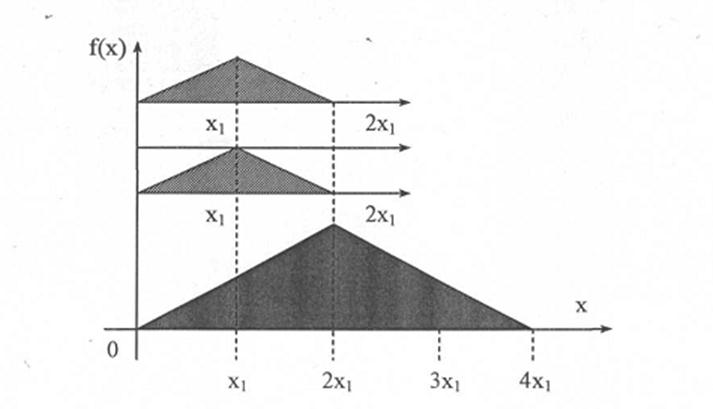
Рис.2.5. Распределение плотности вероятности по нормальному закону

          Очевидно, что сумма четырех случайных величин с равновероятностным распределением и одинаковыми областями рассеивания аккумулирует распределение, близкое к нормальному. Это важное обстоятельство для практики свидетельствует о том, что нормальным законом аппроксимируется распределение выходного параметра устройства, если он зависит от определенного числа параметров, хотя бы более четырех. Если выходной параметр устройства описывается двумя или тремя показателями, случайная величина каждого из которых имеет распределение отличное от нормального, то аппроксимацией пользоваться крайне некорректно. Этим обстоятельством и объясняется то, что практически большинство выходных параметров устройств подчиняются закону нормального распределения. Выходные параметры устройств имеют некоторые средние величины и определенные их разбросы, которые регламентируются определенными отклонениями – допусками. Характерно, что разброс параметров устройств в сложных эксплуатационных условиях может оказаться значительно больше, чем указываемые в ТЗ.

          Очередным обоснованием возможности использования нормального закона распределения значений параметра при разработке ЭС является следующий важный аспект. На величины соответствующего параметра в процессе достижения его соответствующего уровня качества влияет множество факторов, в том числе такие как:

·  неточности технологических режимов;

·  погрешности технологической оснастки;

·  ошибки на уровне человеческих факторов;

·  необходимость учета реальных условий эксплуатации ЭС, т. е.

влияние как внешних, так и внутренних дестабилизирующих факторов и т. д.

          В целом это соприкасается с центральной предельной теоремой вероятности, как множество факторов, влияющих на величину соответствующего параметра в процессе производства ЭС.