Поскольку критерий ПЭ как член аргумента функции Лапласа
находится в прямой пропорциональной зависимости ![]() .
Из рис. 3.1 очевидно, что в функции связи критерия ПЭ с вероятностью
его достижения можно выделить три участка. В начале рабочего участка, т.е. в
близи допустимого значения критерия ПЭ, вероятность его достижения крайне мала.
В середине рабочего участка наблюдается существенные возрастания критерия ПЭ.
На третьем участке функции связи, скорость роста критерия ПЭ замедляется, а
вероятность достижения критерия ПЭ достигает своей максимальной величины, где
также требуются существенные технические усилия для достижения критерия ПЭ ЭС
на этапах их разработки.
.
Из рис. 3.1 очевидно, что в функции связи критерия ПЭ с вероятностью
его достижения можно выделить три участка. В начале рабочего участка, т.е. в
близи допустимого значения критерия ПЭ, вероятность его достижения крайне мала.
В середине рабочего участка наблюдается существенные возрастания критерия ПЭ.
На третьем участке функции связи, скорость роста критерия ПЭ замедляется, а
вероятность достижения критерия ПЭ достигает своей максимальной величины, где
также требуются существенные технические усилия для достижения критерия ПЭ ЭС
на этапах их разработки.
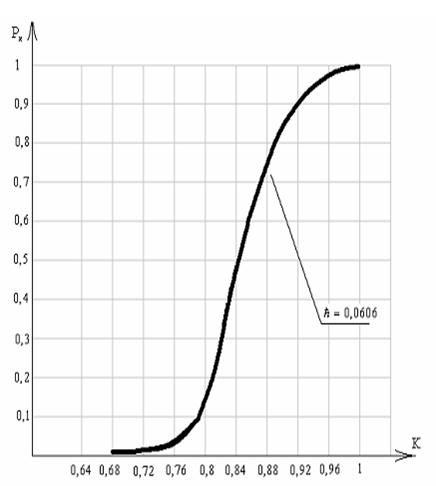
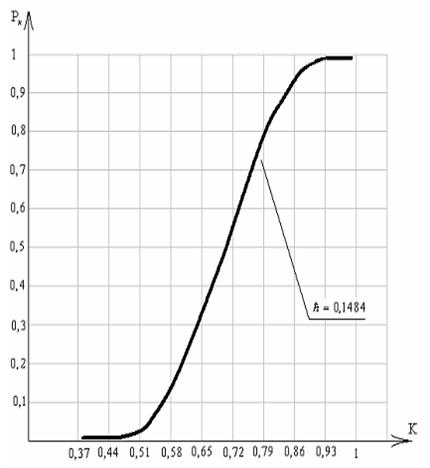
Рис. 3.1 Зависимость критерия ПЭ ЭС Рис.3.2 Зависимость критерия ПЭ ЭС
от вероятности его достижения для от вероятности его достижения для
рабочего участка функции качества всего участка функции качества
3.2 Функция количественной связи достигнутого уровня критерия ПЭ ЭС с плотностью распределения данного критерия
Для построения графической зависимости распределения плотности критерия ПЭ от достигнутого его уровня используется вероятностная модель в нормированном виде
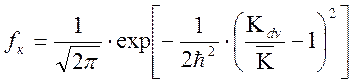 ,
,
Заметим, что такой показатель
надёжности в производственных условиях используется несколько реже, чем другие
характеристики. Однако в решении данной задачи целесообразно рассмотреть и
данный показатель надёжности в связи с критерием ПЭ ЭС. При этом вид
графической зависимости распределения плотности критерия ПЭ для обоих участков
функции качества практически одинаковы. Поэтому рассмотрим зависимость ![]() , для рабочего участка функции
качества. Основными исходными данными для расчёта являются:
, для рабочего участка функции
качества. Основными исходными данными для расчёта являются:
![]() среднее значение функции
качества
среднее значение функции
качества
![]() ,
,
![]() среднеквадратическое
отклонение критерия
среднеквадратическое
отклонение критерия
![]() ,
,
![]() коэффициент
технологической изменчивости
коэффициент
технологической изменчивости
![]() .
.
Результаты расчётов сведены в таблицу
3.3. Графическая зависимость ![]() представлена на
рис.3.3. Данную функцию можно представить и в зависимости от аргумента функции
Лапласа. При этом она будет иметь совершенно одинаковый вид с построенной
функцией. На рис.3.3. очевидно, что функция распределения
плотности критерия ПЭ обладает островершинностью и имеет не слишком резкий
спад. При этом точки распределения функции симметричны относительно
вертикальной оси среднего значения критерия ПЭ.
представлена на
рис.3.3. Данную функцию можно представить и в зависимости от аргумента функции
Лапласа. При этом она будет иметь совершенно одинаковый вид с построенной
функцией. На рис.3.3. очевидно, что функция распределения
плотности критерия ПЭ обладает островершинностью и имеет не слишком резкий
спад. При этом точки распределения функции симметричны относительно
вертикальной оси среднего значения критерия ПЭ.
Подчеркнём, что в данном случае важным является то, через какие значения критерия ПЭ связываются между собой такими показателями надёжности как вероятность достижения критерия ПЭ и плотность этого критерия.
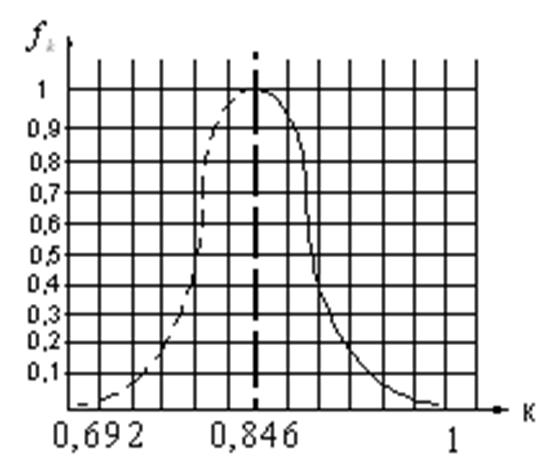
Рис.3.3 Плотность распределения критерия ПЭ ЭС
3.3 Функция количественной связи достигнутого уровня критерия ПЭ ЭС с опасностью отказов данного критерия
Для построения графической зависимости распределения опасности отказов критерия ПЭ от достигнутого его уровня используется вероятностная модель
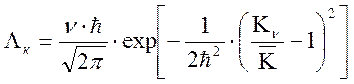
Ранее отмечалось, что если все
параметры ЭС находятся в допустимых пределах, от его состояния считается работоспособным.
Если хотя бы один из параметров ЭС вышел за допустимые пределы, то это
состояние считается неработоспособным. В данном случае нижним допустимым
пределом является величина критерия ПЭ, равная 0,6921. Однако исследование
модели ![]() можно проводить для всего участка
существование функции качества, но при этом использовать результаты только
рабочего его участка.
можно проводить для всего участка
существование функции качества, но при этом использовать результаты только
рабочего его участка.
Основными исходными данными для расчётов являются:
![]() среднее значение
критерия ПЭ:
среднее значение
критерия ПЭ:
![]() ,
,
![]() среднеквадратические
отклонения критерия ПЭ:
среднеквадратические
отклонения критерия ПЭ:
![]() ,
,
![]() коэффициент
технологической изменчивости:
коэффициент
технологической изменчивости:
![]() .
.
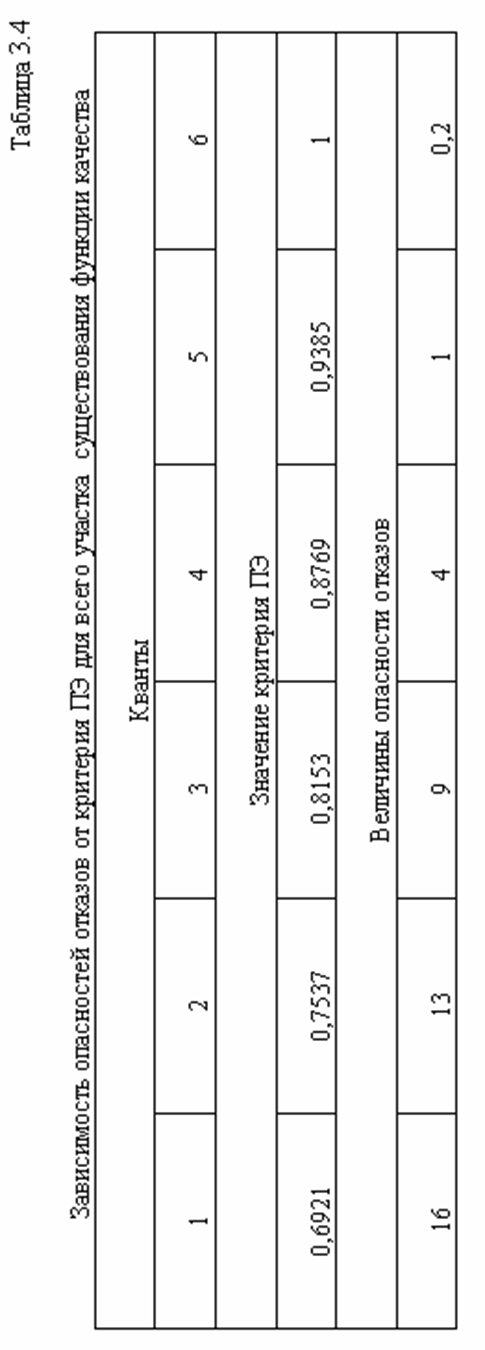
Результаты расчётов приведены в таблицу 3.4, графическая зависимость показана на рис.3.4. Из рис.3.4 замечаем следующие особенности:
![]() на границе допустимого
значения критерия ПЭ ЭС опасность отказов достаточно велика,
на границе допустимого
значения критерия ПЭ ЭС опасность отказов достаточно велика,
![]() по мере роста критерия ПЭ
опасность отказов монотонно уменьшается,
по мере роста критерия ПЭ
опасность отказов монотонно уменьшается,
![]() по достижению наилучшего
значения критерия ПЭ опасность отказов достигает наименьшей своей величины.
по достижению наилучшего
значения критерия ПЭ опасность отказов достигает наименьшей своей величины.
В целом это достаточно хорошо согласуется с пониманием данных показателей с практикой процесса разработки ЭС.
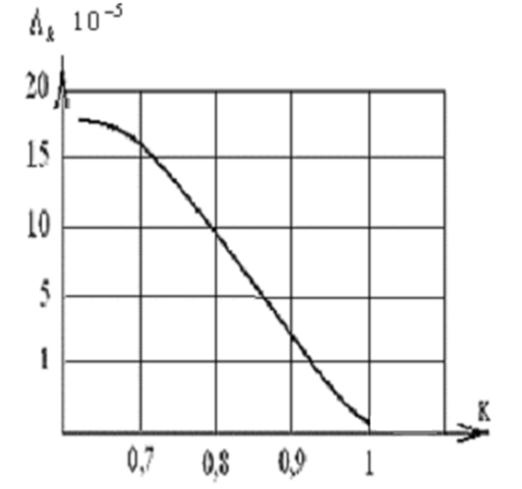
Рис. 3.4 Зависимость опасности отказов от достигнутого
уровня критерия ПЭ
3.4 Функция количественной связи достигнутого уровня критерия ПЭ ЭС со средним временем безотказной работы
Для построения графической зависимости среднего времени безотказной работы от достигнутого уровня критерия ПЭ ЭС используются вероятностные модели
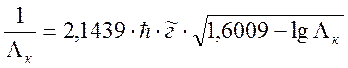
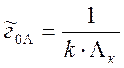
Строить данную зависимость целесообразно для всего участка существования функции качества, но при этом использовать результаты только для рабочего её участка. Основными исходными данными для расчётов являются:
![]() среднее значения критерия
ПЭ:
среднее значения критерия
ПЭ:
![]() ,
,
![]() среднеквадратичное
отклонение критерия ПЭ:
среднеквадратичное
отклонение критерия ПЭ:
![]() ,
,
![]() коэффициент
технологической изменчивости:
коэффициент
технологической изменчивости:
![]() ,
,
![]() опасности отказов
достигнутого уровня критерия ПЭ:
опасности отказов
достигнутого уровня критерия ПЭ:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Затем, используя вероятностные модели
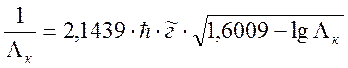
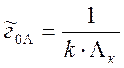
Получаем частные математические модели связи среднего времени безотказной работы со средним временем безотказной работы в нормированном виде. Они записываются так:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Рассчитав величины ![]() , получаем
значения среднего времени безотказной работы от достигнутого уровня критерия
ПЭ.
, получаем
значения среднего времени безотказной работы от достигнутого уровня критерия
ПЭ.
Количественные составляющие вероятностной модели по квантам
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Результаты расчётов сводятся в таблицу 3.5, графическая
зависимость функции 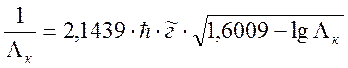 показана на рис.3.5.
показана на рис.3.5.
Из рис.3.5 замечаем следующие особенности:
![]() в начале роста критерия ПЭ
среднее время безотказной работы монотонно возрастает;
в начале роста критерия ПЭ
среднее время безотказной работы монотонно возрастает;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.