Очевидно, что изменение параметра в пределах его граничных значений будет подчиняться ближе всего к закону нормального распределения.
Функционально- математическая связь количественных характеристик надёжности с критерием ПЭ устанавливается с учётом соответствующего закона распределения. При этом на основании сказанного выше используется закон нормального распределения.
Из ранее приведённых исследований, связанных с оценкой качества ЭС на этапе их разработки, известно, что если выполняется условие
![]()
то система не соответствует требованиям ТЗ. Отсюда очевидно, что решать задачу математической интеграции количественных характеристик надёжности с критерием ПЭ необходимо на рабочем участке функции качества (рис.4.1). Однако не рабочий участок функции качества в решении данной задачи также имеет право на существование. Это объясняется следующими обстоятельствами:
![]() не
достаточно высоким техническим уровнем производства;
не
достаточно высоким техническим уровнем производства;
![]() наличием большой
технологической погрешности при разработке ЭС и т.д. Это приведёт к тому, что
критерий ПЭ может выйти за допустимый предел.
наличием большой
технологической погрешности при разработке ЭС и т.д. Это приведёт к тому, что
критерий ПЭ может выйти за допустимый предел.
Поэтому решать данную задачу целесообразно не только для рабочего участка, но и для всего участка существования функции качества. Это позволит получить наиболее полную информацию решаемой задачи.
Исходя из данных соображений, имеем
следующие соотношения соответственно как для рабочего, так и для всего
участков функции качества. Наилучшее значение критерия ПЭ равно ![]() ,
,
![]() нижние
допустимые величины критерия ПЭ, соответственно для рабочего участка и для
всего участка функции:
нижние
допустимые величины критерия ПЭ, соответственно для рабочего участка и для
всего участка функции:
![]() ;
; ![]() ,
,
![]() интервалы функций качества,
соответственно для рабочего участка и для всего участка функции:
интервалы функций качества,
соответственно для рабочего участка и для всего участка функции:
![]() ;
; ![]() ,
,
![]() половины интервалов функций
качества, соответственно для рабочего участка и для всего участка функции:
половины интервалов функций
качества, соответственно для рабочего участка и для всего участка функции:
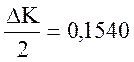 ;
; 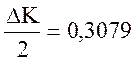 ,
,
![]() средние величины критерия
ПЭ, соответственно для рабочего участка и для всего участка функции:
средние величины критерия
ПЭ, соответственно для рабочего участка и для всего участка функции:
![]() ;
; ![]() ,
,
поскольку 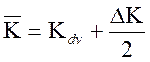 .
.
Далее исходим из следующих соображений:
![]() из
шести среднеквадратических отклонений на интервале функции качества;
из
шести среднеквадратических отклонений на интервале функции качества;
![]() из
десяти квантов на интервале функции качества.
из
десяти квантов на интервале функции качества.
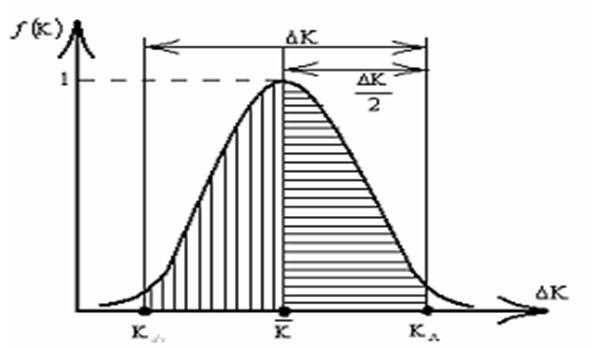
Рис.2.6. Зависимость плотности критерия ПЭ от величины его квантов
Сказанное выше показано на рис.2.6., отражающий зависимость плотности критерия ПЭ от величин его квантов.
Затем рассчитываются следующие величины соответственно для рабочего и всего участков функции качества:
![]() среднеквадратическое
отклонение, приходящееся на один квант:
среднеквадратическое
отклонение, приходящееся на один квант: ![]()
![]() ,
, ![]() ,
,
![]() критерий
ПЭ, приходящийся на один квант,
критерий
ПЭ, приходящийся на один квант,
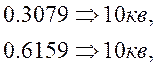
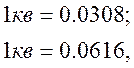
![]() среднеквадратичное отклонение
критерия ПЭ
среднеквадратичное отклонение
критерия ПЭ
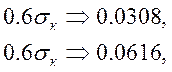
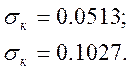
Из проведённых расчётов, очевидно, что среднеквадратическое отклонение критерия ПЭ для всего участка существования функции качества заметно больше, чем для рабочего участка.
Затем рассчитываются граничные значения квантов критерия ПЭ соответственно для рабочего и всего участков функции качества:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Зная величины ![]() и
и
![]() не трудно получить граничные
значения квантов критерия ПЭ в количественном виде. Результаты расчётов
сведены в таблицу.
не трудно получить граничные
значения квантов критерия ПЭ в количественном виде. Результаты расчётов
сведены в таблицу.
Таблица 2.1
Граничные значения квантов критерия ПЭ
|
Кванты |
Граничные значения квантов |
|
|
Рабочий участок |
Весь участок |
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
2.3 Построение вероятностных моделей связи характеристик надёжности с критерием ПЭ ЭС.
Известно, что параметрическая надёжность (критериальная) определяется как вероятность нахождения определяющего параметра устройства в заданных пределах. Это обеспечивает точность работы функционального устройства. В практике чаще всего определяющим параметром является значение выходного параметра устройства. Однако для решения данной задачи в качестве выходного параметра устройства целесообразно использовать критерий ПЭ ЭС, который обеспечивает функциональную связь параметров, относящихся к различным свойствам качества ЭС. Это обеспечивает наиболее полное математическое описание ЭС на этапе их разработки.
Тогда вероятность попадания критерия
ПЭ распределённого по закону нормального распределения, в пределах ![]() или
или ![]() определяется
так:
определяется
так:
![]() если
если
![]() то имеем
то имеем
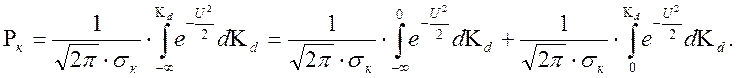
![]()
Величина 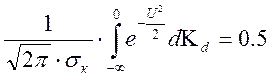 – как интеграл
Эйлера.
– как интеграл
Эйлера.
В результате получаем:
![]() ,
,
где U– аргумент функции Лапласа, Ф(U)– функция Лапласа.
![]()
![]() если
если
![]() , то имеем
, то имеем
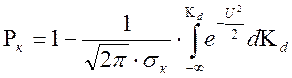 .
.
В результате получаем
![]()
![]()
При этом:
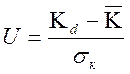 .
.
Далее обратимся к показателям надёжности. При этом выделим следующие количественные характеристики надёжности:
![]() вероятность
доступного уровня критерия ПЭ
вероятность
доступного уровня критерия ПЭ
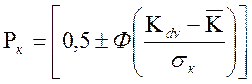 (2.6)
(2.6)
Поскольку проводимые исследования связаны с нижним допустимым пределом критерия ПЭ, то в выражении (2.6) необходимо использовать положительный знак. Характерно, что каждому конкретному предприятию электронной промышленности соответствует определённый коэффициент технологической изменчивости. Это обосновывается соответствующим технологическим уровнем производственного оборудования и оснастки.
![]() плотность
распределения достигнутого уровня критерия ПЭ
плотность
распределения достигнутого уровня критерия ПЭ
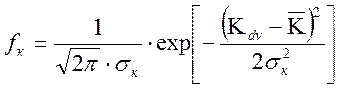 (2.7)
(2.7)
![]() опасность отказов
достигнутого уровня критерия ПЭ
опасность отказов
достигнутого уровня критерия ПЭ
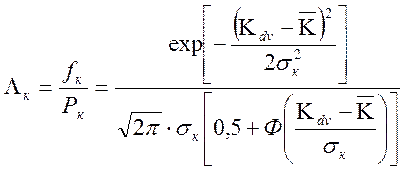 (2.8)
(2.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.