Разработка и исследование дискретной системы автоматического регулирования, страница 6

13 Определение устойчивости САР по аналогу критерия Михайлова

Для устойчивости ДСАР необходимо и достаточно, чтобы годограф вектора ХУ при изменении частоты от 0 до p/T, начинаясь на положительной вещественной полуоси, обходил последовательно и монотонно в положительном направлении 2n квадратов, где n – это степень ХУ.

Степень ХУ – 4, таким образом, годограф должен пройти  квадрантов.

Для построения кривой Михайлова в дискретной системе необходимо в ХУ произвести замену :

В полученном выражении выделим вещественную  и мнимую  части с использованием формулы Эйлера:

Воспользуемся формулой Эйлера, тогда из полученного характеристического уравнение выделим действительную и мнимую часть.

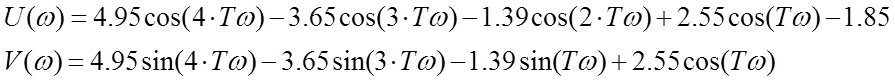
Тогда на диапазоне частот от  получим численное значение действительной и мнимой частей, приведенных в таблице 1.

Таблица 1

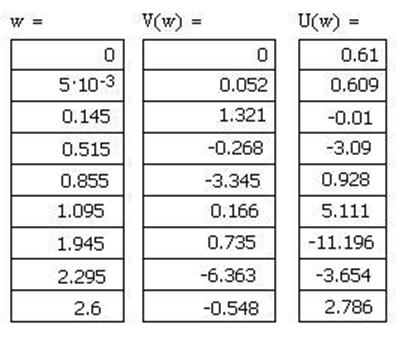
По данным таблицы 1 строим годограф Михайлова (рисунок 13.1):

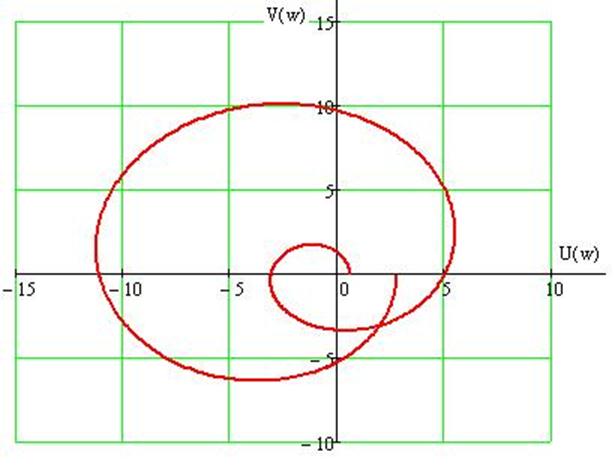
Рисунок 13.1 - График кривой Михайлова

Так как кривая Михайлова (рисунок 13.1), начинаясь на положительной полуоси, обходит восемь квадрантов в положительном направлении, то данная ДСАУ по аналогу критерия Михайлова устойчива.

14 Определение устойчивости САР по аналогу критерия Найквиста

Если разомкнутая дискретная система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф вектора , при изменении частоты ω от 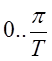, не охватывал точку с координатами (-1; j0).

Для построения АФХ разомкнутой ДСАР необходимо в Z-ПФ разомкнутой системы  произвести подстановку :

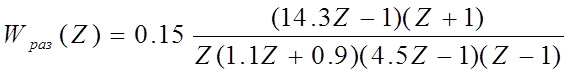
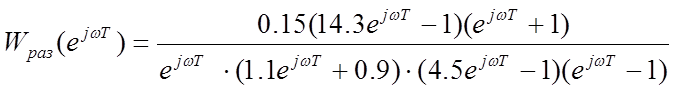
В полученном выражении выделим вещественную  и мнимую  части с использованием формулы Эйлера:

Тогда ПФ разомкнутой ДСАР примет вид:

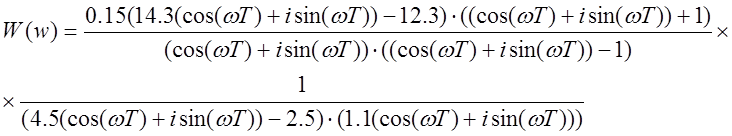
  Задаваясь значениями частоты  от 0 до , вычисляются соответствующие значения вещественной  и мнимой  частей частотной функции и на комплексной плоскости строится АФХ разомкнутой САР.

  Численное значение действительной и мнимой частей приведены в таблице 2.

Таблица 2

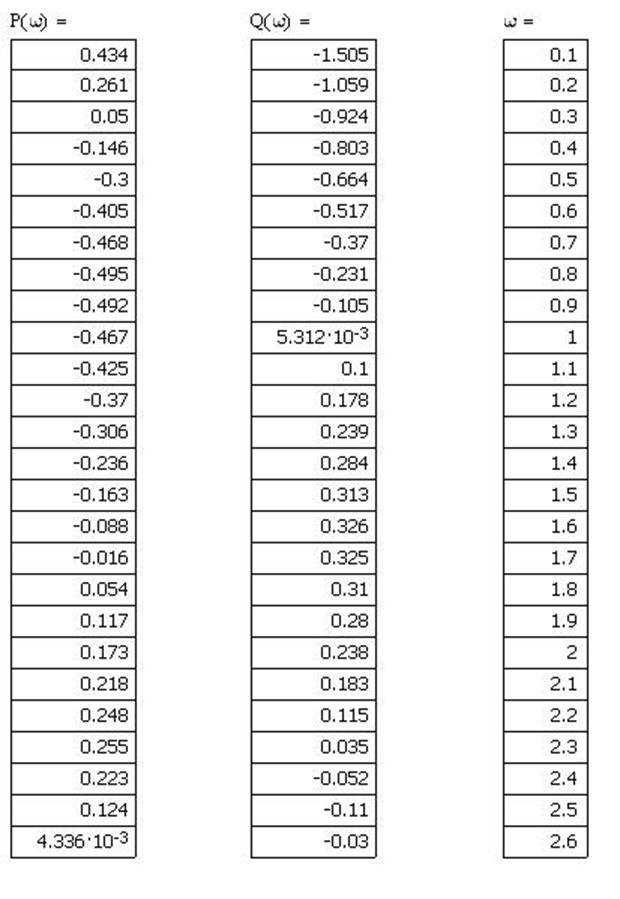
По данным таблицы 2 строим АФХ (рисунок 14.1):

 

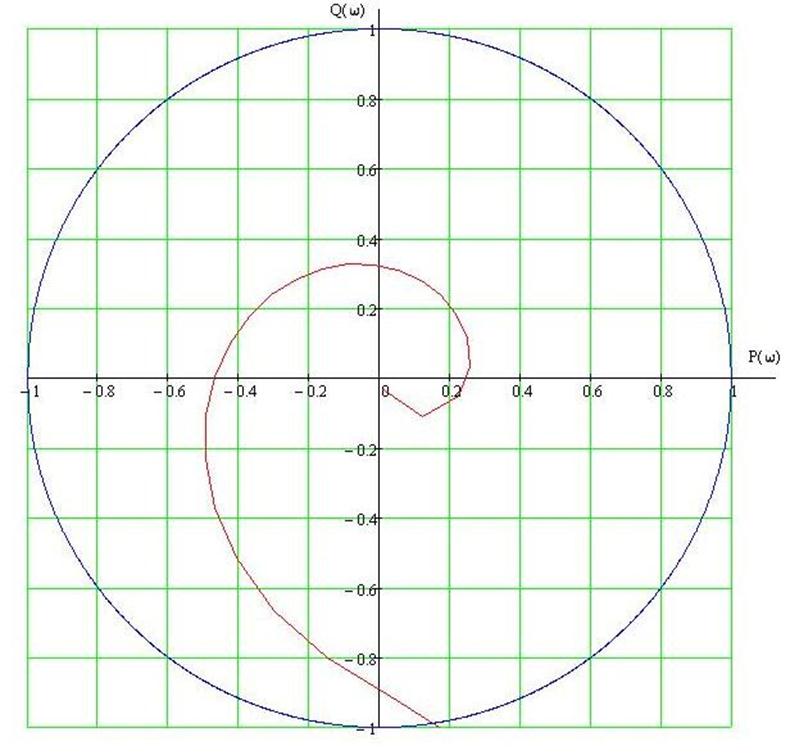
Рисунок 14.1 - График АФХ

Определим запасы устойчивости по АФХ (рис. 14.1):

Запас по амплитуде это величина обратная величине радиус вектора выходящего с начала координат в точку пересечения АФХ с окружностью единичного радиуса на отрицательной вещественной полуоси.

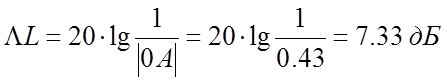
По фазе это угол между этим радиусом проведенным через точку пересечения АФХ с окружностью единичного радиуса и  отрицательной вещественной полуоси.

Так как годограф вектора (рисунок 14.1) при изменении частоты w от 0 до p/T не охватывает точку (-1;j0) –  данная ДСАУ по аналогу критерия Найквиста устойчива.

15 Построение графика переходного процесса САР

 

Переходной характеристикой ДСАР называется график изменения выходной (регулируемой) величины системы во времени Xвых(t), если входному (возмущающему или задающему) воздействию соответствует единичная ступенчатая решетчатая функция

Z-ПФ замкнутой ДСАР имеет вид:

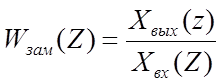
С учетом того, что

,

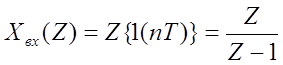Z – изображение переходной характеристики примет вид

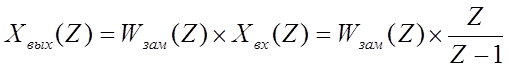
Полученное выражение имеет форму отношения полиномов

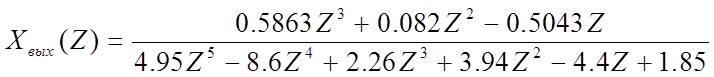
Поделим числитель на знаменатель и полученные значения будут являются ординатами переходного процесса.

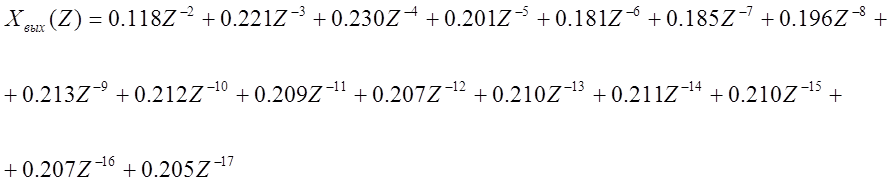
Построим переходной процесс (рисунок 15.1)

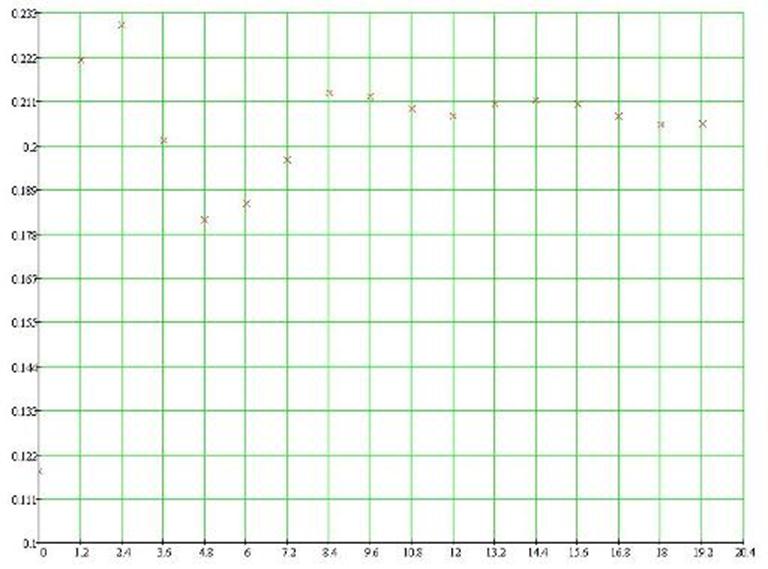
Рисунок 15.1 - Переходной процесс ДСАР

16 Определение прямых показателей качества

Качество САР определяет характер затухания переходного процесса устойчивой системы. Величины, характеризующие поведение САР в переходном процессе, вызванном типовым внешним воздействием, называются показателями качества системы. Существуют прямые и косвенные показатели качества. Оценки качества, получаемые непосредственно из анализа кривой переходного процесса называются прямыми показателями качества. Косвенные показатели позволяют определить характер переходного процесса без построения его графика (корневые – по расположению корней характеристического уравнения на комплексной плоскости).

     Прямые показатели качества

Время регулирования  определяется промежутком времени от начала переходного процесса до того момента, когда регулируемая величина  будет отличаться от своего установившегося значения  меньше, чем на некоторую заданную величину . Величина  принимается равной 0,05. Полосу шириной , определяющую практическое завершение переходного процесса, принято называть “трубкой переходного процесса”

Максимальное отклонение (динамическая ошибка системы)  регулируемой величины от установившегося значения . Для переходного процесса (колебательного статического),  вводится специальный показатель качества – перерегулирование . За количественную меру перерегулирования принимается отношение максимального отклонения регулируемой величины   к установившемуся значению , выраженное в процентах

.

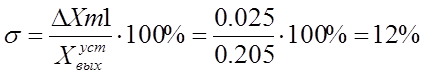Величина  в САР обычно не должна превышать 10–30%. Следовательно по этому показателю наша САР устойчива.

 Установившаяся (статическая) ошибка системы  – это отклонение фактического установившегося значения регулируемой величины  от заданного значения.

 При наличии установившейся ошибки САР и регулятор называются статическими, при её отсутствии – астатическими.

В нашем случае САР статическая и

 Колебательность САР характеризуется числом колебаний  регулируемой величины около линии установившегося значения за время переходного процесса.

.

Колебательность переходного процесса может также оцениваться степенью затухания , равной отношению разности амплитуд отклонения регулируемой величины в первый полупериод  и амплитуде второго полупериода к амплитуде отклонения регулируемой величины в первый полупериод

.

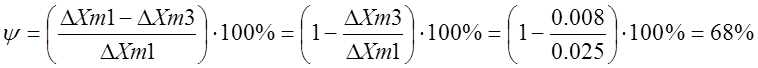17 Мультимикропроцессорные системы