Разработка и исследование дискретной системы автоматического регулирования, страница 5

Получаем ЛЧХ скорректированной разомкнутой системы  и , которая изображена  на рис.8.2 зеленым цветом. С помощью графика на рис.8.1 строим “запретную область” для ЛФЧХ разомкнутой САР при М=1,5. “Запретную область” на рис.8.2 заштрихована и ЛФЧХ скорректированной разомкнутой САР не заходит в нее.

Определяем запасы устойчивости.

Запас устойчивости - это мера удаления характеристик САР от границы устойчивости. Запас устойчивости по фазе определяется абсолютной величиной угла, который дополняет ЛФХ при частоте среза ЛАХ до -180°. В нашем случае Δφ=90°

Для определения запаса устойчивости по амплитуде необходимо найти точку пересечения ЛФХ с линией -180°. Из точки пересечения восстановить перпендикуляр к оси абсцисс. Запас по амплитуде будет расстоянием между L_Р и осью абсцисс. В нашем случае DL=9 дБ.

 

 

Рисунок 8.2 - Логарифмические частотные характеристики                                   разомкнутой ДСАР

ПФ скорректированной разомкнутой ДСАР примет вид:

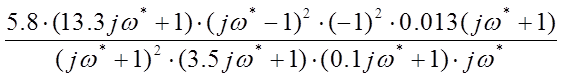
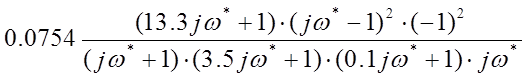
Чтобы определить Z-ПФ скорректированной разомкнутой ДСАР, необходимо ввести замену:

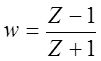
Тогда Z-ПФ скорректированной разомкнутой ДСАР примет вид:

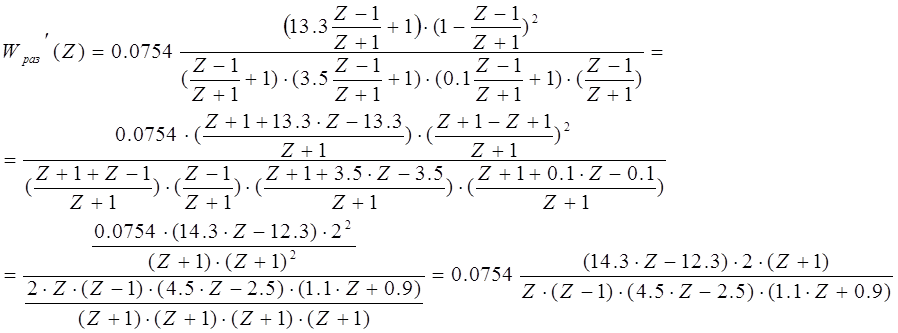
Для определения Z-ПФ скорректированной прямой цепи необходимо Z-ПФ скорректированной разомкнутой ДСАР разделить на ПФ ИЭ:

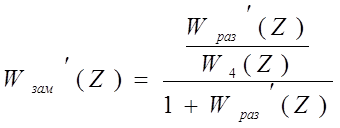
Теперь Z-ПФ замкнутой скорректированной ДСАР примет вид:

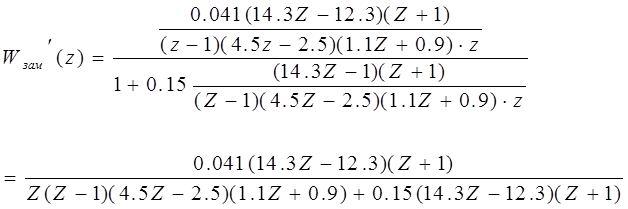
9 Определение устойчивости дискретной САР по Z-корневому критерию

Устойчивость САР – это способность системы возвращаться в исходное равновесное состояние или занимать новое состояние равновесия после прекращения действия внешнего возмущения.

Сущность корневого критерия состоит в том, что ДСАР будет устойчивой, если все корни Zi характеристического уравнения по модулю меньше единицы | Zi | < 1,  то есть если корни ХУ на комплексной плоскости (Z – плоскости) будут лежать внутри круга единичного радиуса. Система, не удовлетворяющая этому условию, является неустойчивой.

Приравнивая знаменатель Z-ПФ замкнутой ДСАР к нулю, получим ХУ:

.

Корни данного ХУ:

Расположения корней устойчивой дискретной САР в плоскости Z  показано на рисунке 9.1.

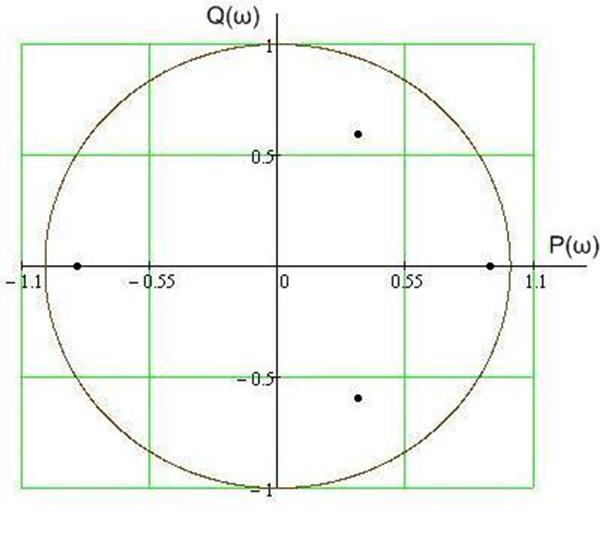
Рисунок 9.1 - Расположение корней характеристического уравнения

на комплексной плоскости Z

Следуя с условия корневого критерия, данная САР является устойчивой, так как все корни характеристического уравнения попали в единичную окружность и модуль | Zi | < 1.

10 Определение устойчивости по w-корневому критерию. Определение косвенных показателей  качества

Для устойчивости ДСАР необходимо и достаточно чтобы все корни w- преобразованного уравнения были отрицательными, а все комплексные корни имели отрицательную вещественную часть.

Согласно теории функций комплексного переменного с помощью билинейного преобразования

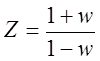
единичный круг в комплексной плоскости Z отображается в левую часть комплексной плоскости w. Поэтому в характеристическом уравнении:

Вместо Z  подставляем в ХУ САР выражение 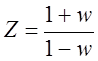. Получаем:

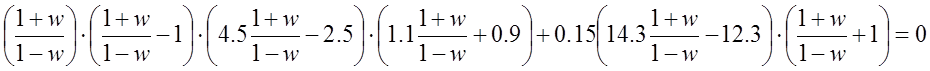
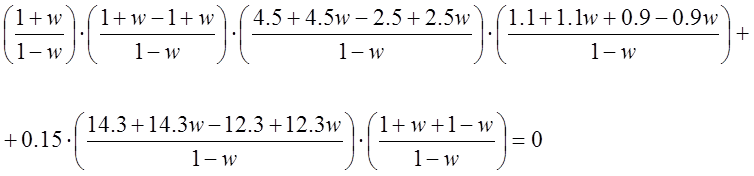
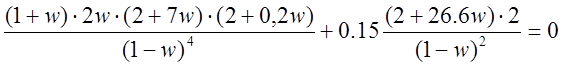
После приведения к общему знаменателю и его отбрасывания получаем новое w-характеристическое уравнение того же порядка:

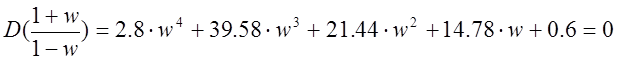
Используя программу “Mathcad” находим корни характеристического уравнения:

;

Изобразим корни преобразованного характеристического уравнения на комплексной w-плоскости и определим косвенные показатели качества (рисунок 10.1):

 

 Рисунок 10.1 - Корни характеристического уравнения

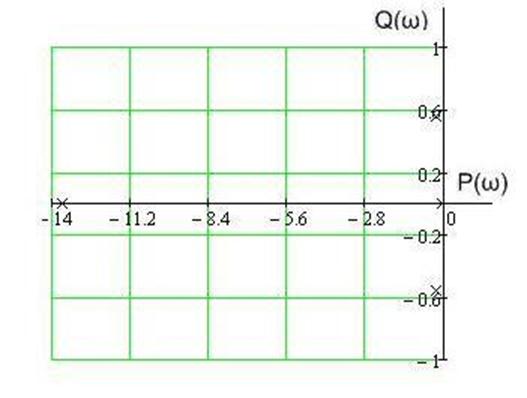
на комплексной w-плоскости

Чтобы определить косвенные показатели качества, необходимо построить расположение ближайшего к мнимой оси корня или комплексно сопряженных корней. Мерой запаса устойчивости системы или косвенными показателями есть:

1)  степень устойчивости, h=0.043;

2)  степень колебательности,  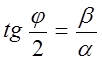, где

φ  - это угол, образуемый лучами, проведёнными из начала координат через ближайшие к мнимой оси комплексные сопряжённые корни.

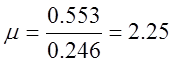
Так как все корни w-преобразованного уравнения отрицательны

(лежат в отрицательной части вещественной оси), что соответствует условиям устойчивости  САР, то можно утверждать, что данная система устойчива по данному критерию. Благодаря применению w-преобразования все критерии устойчивости, разработанные для анализа непрерывных систем, могут быть использованы для анализа устойчивости дискретных систем.

11 Определение устойчивости дискретной САР по аналогу критерия Гурвица

Для устойчивости замкнутой САР n-го порядка необходимо и достаточно, чтобы все коэффициенты w-ХУ уравнения были положительными и n определителей Гурвица, составленных из коэффициентов w-преобразованного ХУ

также были положительными.

Порядок составления определителя Гурвица:

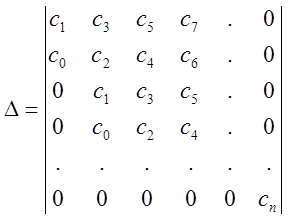
Запишем w-ХУ:

Соответственно коэффициенты ХУ равны:

                                    

Найдем все определители:

;

;

;

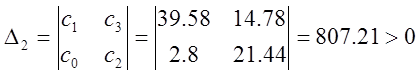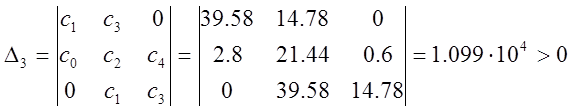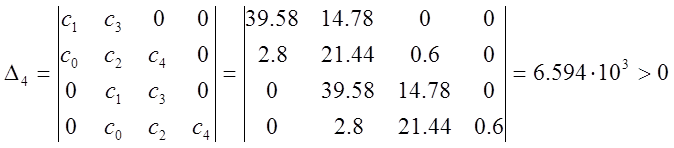
Как видно, все определители, составленные из коэффициентов  w - преобразованного ХУ, больше нуля. Таким образом, можно сделать вывод, что по аналогу критерия Гурвица данная САР  устойчива.

12 Определение устойчивости САР по критерию Шура - Кона

Для устойчивости ДСАУ n-го порядка необходимо и достаточно, чтобы n определителей, составленных из коэффициентов Z-ХУ

были положительными.

Правило составления определителей:

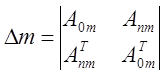, где m=1, 2, … , n

         

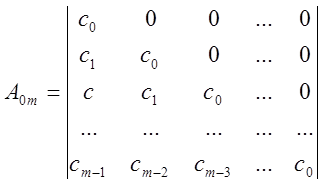
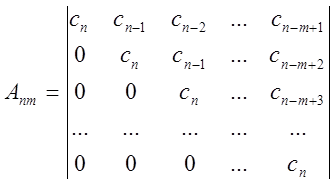
,  - транспонированные матрицы.

;   ;   ;   .

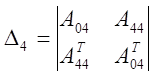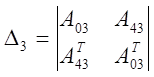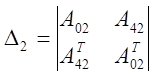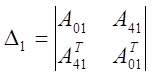ХУ имеет вид:

С помощью среды MathCAD произведем следующие действия:

;         ;         ;        ;        

;           ;                ;           

     

                                 

                  

                              

                              

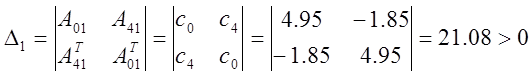
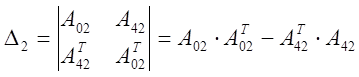
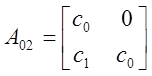
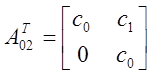
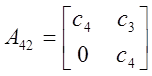
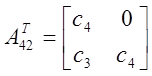
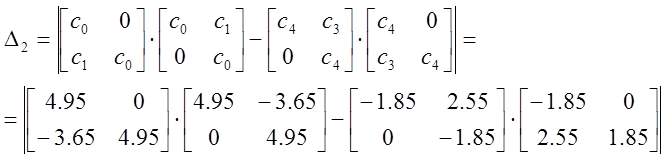
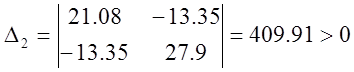
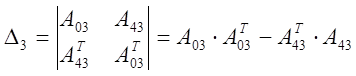
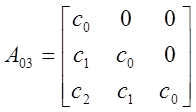
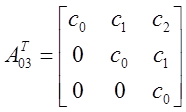
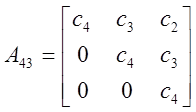
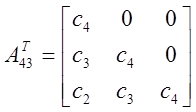
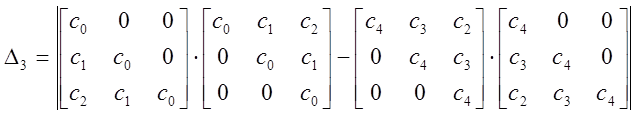
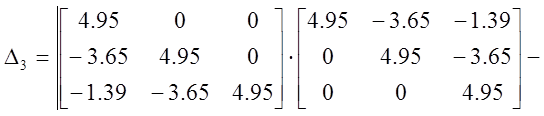
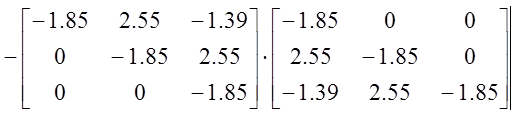
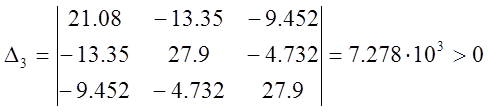
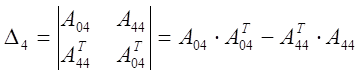
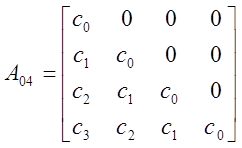
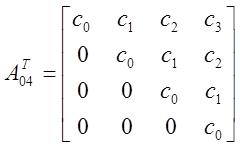
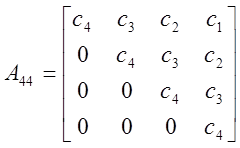
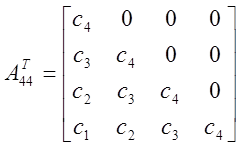
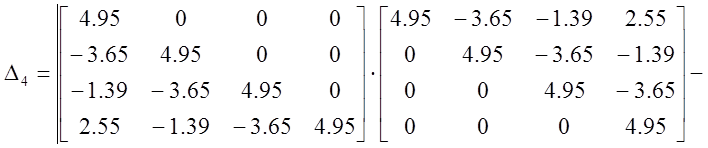
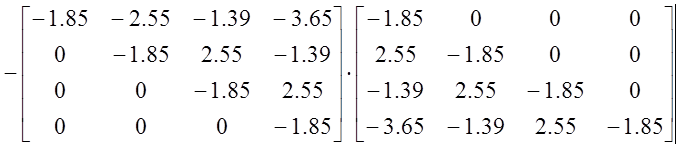
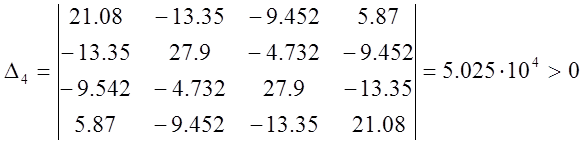
Как видно, все определители больше нуля. Таким образом, можно сделать вывод, что по критерию Шура-Кона данная САР  устойчива.