8) Аналого-цифровой преобразователь (АЦП)
Уравнение:
![]()
Передаточная функция:
![]()
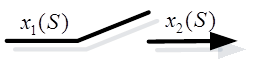
Рисунок 5.8 - Элементарная структура АЦП
9) Цифровое вычислительное устройство с передаточными функциями
Передаточная функция вычислительного устройства
складывается из передаточной функции П - закона регулирования Wзр(S) ,
реализуемого устройством, и передаточной функции звена запаздывания ![]() (Приложение Г).
(Приложение Г).
- закон регулирования:
![]()
![]()
- звено запаздывания:
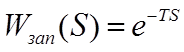
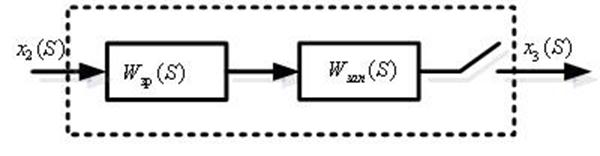
Рисунок 5.9 - Элементарная структура ВУ
10) Передаточная функция формирующего элемента (ЦАП)
Передаточная функция формирующего элемента (ЦАП)
Wфэ(S) с прямоугольной формой импульса и скважностью ![]() (Приложение
Д).
(Приложение
Д).
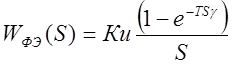
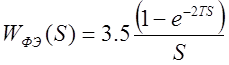
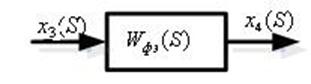
Рисунок 5.10 - Элементарная структура ЦАП
Структурная схема с передаточными функциями замкнутой САР составляется путем согласования изображений входных и выходных сигналов элементарных структур.
Структурная схема с передаточными функциями имеет вид (рисунок 5.11):
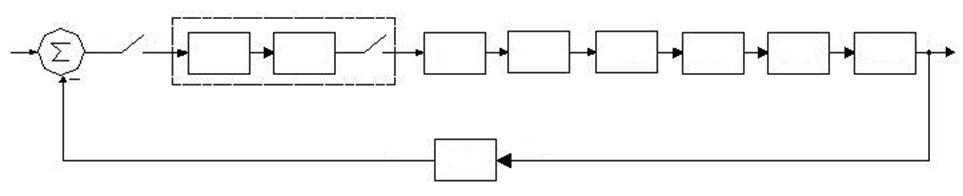 Рисунок 5.11 -
Структурная схема с ПФ замкнутой ДСАР
Рисунок 5.11 -
Структурная схема с ПФ замкнутой ДСАР
Структурная схема разомкнутой САР получается из схемы замкнутой системы путем размыкания главной обратной связи и исключения входных воздействий в систему. Размыкание необходимо производить таким образом, чтобы на входе разомкнутой системы находился импульсный элемент (идеальный ключ). Структурная схема разомкнутой САР представлена на рисунке 5.12

Рисунок 5.12 - Структурная схема с ПФ разомкнутой ДСАР
6 Определение Z-ПФ замкнутой и разомкнутой САР
Переход от передаточных функций элементов и их соединений к Z – передаточным функциям осуществляется с помощью таблицы Z – преобразований (Приложение Б).
Для нахождения ПФ разомкнутой САР воспользуемся рисунком 5.12
Выражения разомкнутой Z-ПФ:
![]()
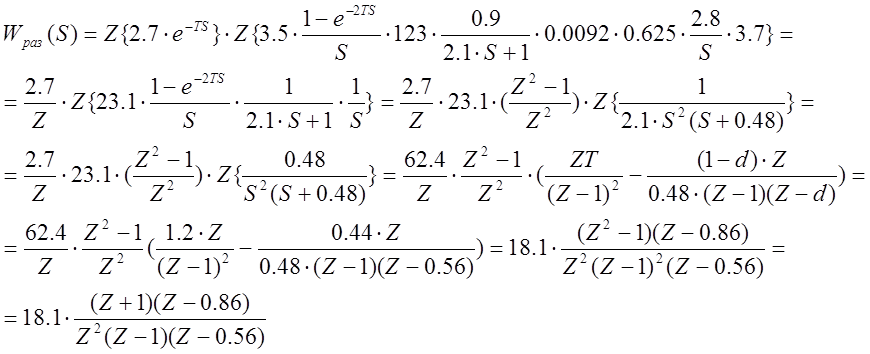
ПФ замкнутой системы находится по следующей формуле с учетом элементов главной отрицательной обратной связи (ООС):
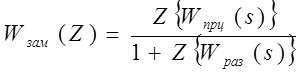
Находим ПФ прямой цепи (рисунок 5.1):
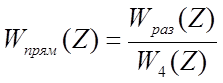
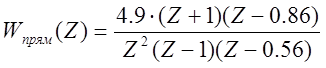
Тогда Z-ПФ замкнутой САР:
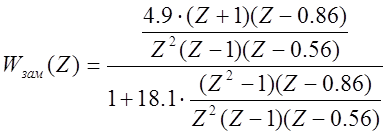
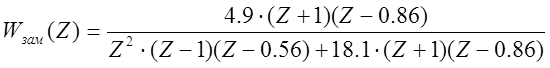
7 Расчет эквивалентной схемы аналогового регулирующего блока
Корректирующий элемент представляет собой звено со специально подобранной ПФ, которая необходима для формирования требуемого закона регулирования.
Согласно заданию КП, КЭ включен в регулирующий блок последовательно с усилителем и имеет ПФ вида:
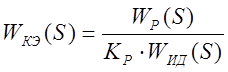
ПФ регулятора для П – закона регулирования имеет вид:
![]()
Тогда
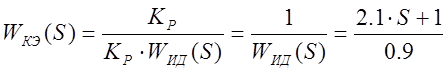
![]()
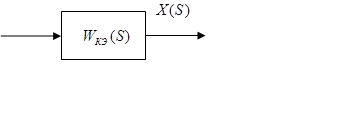
Рисунок 7.1 – Элементарная структура корректирующего элемента
Используя обратное преобразование Лапласа, найдем дифференциальное уравнение корректирующего элемента:
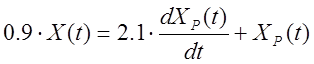
Структурная схема регулятора будет иметь вид:

Рисунок 7.2 – Структурная схема регулятора
Произведем проверку реализации рабочим блоком заданного закона регулирования.
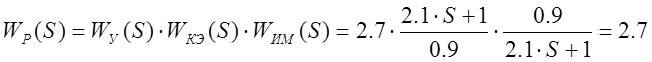
Таким образом, видно, что рабочий блок реализует заданный П-закон регулирования.
8 Определение устойчивости САР с помощью логарифмического критерия устойчивости. Произведение коррекции в случаи неустойчивости. Определение запасов устойчивости
Для устойчивости замкнутой ДСАР необходимо и достаточно чтобы число переходов фазовой характеристики разомкнутой ДСАР через прямую φ=-180ْ снизу вверх было равно числу переходов сверху вниз в интервале частот, где логарифмическая амплитудная характеристика разомкнутой системы положительна.
Показатели качества ПП для дискретных САР, как и в случае непрерывных систем, обычно определяются при отработке системой единичного ступенчатого воздействия. При синтезе дискретных систем используется также показатель колебательности М, который определяется максимальной величиной ординаты амплитудно-частотной характеристики (АЧХ) замкнутой САР. Для удовлетворительного качества переходного процесса системы показатель колебательности М обычно выбирается в пределах 1,3÷1,7. При разработки дискретной САР задаёмся значением М=1,5.
Для того, чтобы обеспечить заданный показатель колебательности М=1,5, необходимо по графику на рисунке 4.4 построить «запретнуюобласть» для логарифмической фазово-частотной характеристики разомкнутой системы. Если ЛФЧХ не заходит внутрь области в том интервале частот, в котором выполняются неравенства
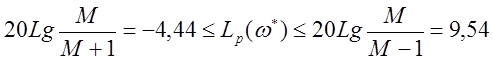 ,
,
то заданный показатель колебательности будет обеспечен.
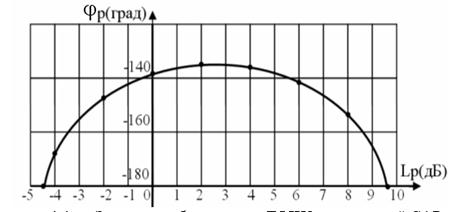
Рисунок 8.1 - «Запретная область» для ЛФЧХ разомкнутой САР при М=1,5
Для применения данного метода к ДСАР необходимо произвести w-преобразование:
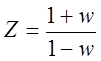
Замену подставляем в Z-ПФ разомкнутой ДСАР:
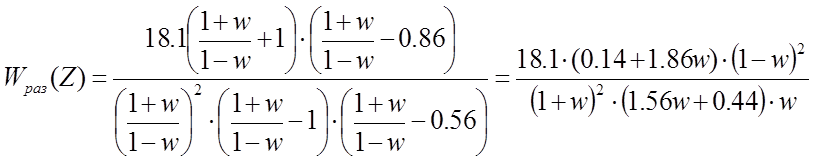
Для построения ЛЧХ произведем замену:
![]()
Получим выражение w-ПФ:
![]()
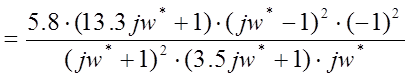
Представим частотную функцию разомкнутой системы в виде произведения типовых сомножителей (Приложение А):
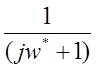 - два апериодических звена первого порядка. Для
- два апериодических звена первого порядка. Для 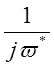 - интегрирующее звено. Для
- интегрирующее звено. Для 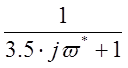 -
апериодическое звено первого порядка. Для
-
апериодическое звено первого порядка. Для Строим
асимптотические логарифмические частотные характеристики типовых звеньев.
Суммируя ординаты ЛЧХ всех множителей, получаем ЛЧХ разомкнутой системы (![]() ) и (
) и (![]() ),
которые изображены на рис. 8.2 красным цветом.
),
которые изображены на рис. 8.2 красным цветом.
Расположение
ЛЧХ показывает, что САР не удовлетворяет ни одному из предъявляемых к ней
требований, поэтому необходимо выполнить коррекцию системы. Для реализации всех
требований к САР ЛАЧХ необходимо переместить влево вдоль оси абсцисс, а ЛФЧХ –
вверх над осью ![]() . Этого можно достичь применением
дифференцирующего корректирующего устройства с ЧФ (Приложение В)
. Этого можно достичь применением
дифференцирующего корректирующего устройства с ЧФ (Приложение В)
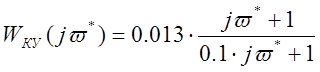
ЛЧХ
корректирующего устройства (![]() ) и (
) и (![]() ) показаны на рис.8.2 синим цветом.
Суммируя ординаты ЛЧХ разомкнутой САР и корректирующего устройства
) показаны на рис.8.2 синим цветом.
Суммируя ординаты ЛЧХ разомкнутой САР и корректирующего устройства
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.