Разработка динамической модели гидравлической системы. Моделирование и анализ статического состояния гидросистемы

СОДЕРЖАНИЕ

1 Исходные данные                                                                                                      2

2 Разработка динамической модели гидравлической системы                                3

2.1 Компонентные и топологические уравнения гидросистемы                             4

2.2 Описание гидросистемы и разработка схемы динамической модели               4

2.3 Построение орграфа гидросистемы                                                                      7

2.4 Составление матрицы инциденций                                                                      9

2.5 Использование узлового метода                                                                         10

2.6 Определение параметров элементов модели                                                     13

2.7 Использование структурно–матричного метода, формирование математической модели                                                                                                           13

3 Моделирование и анализ статического состояния гидросистемы                     16

3.1 Разработка статической модели гидросистемы                                                 16

3.2 Формирование матрицы Якоби в статической модели гидросистемы

3.3 Решение систем уравнений статической модели методом Ньютона              18

4 Моделирование и анализ переходных процессов                                                20

4.1 Формирование матрицы Якоби в динамической модели                                 21

4.2 Выбор параметров интегрирования                                                                    22

4.3 Решение системы дифференциального уравнения методом Эйлера              24

4.3 Решение системы дифференциального уравнения методом Эйлера              27

Приложение А                                                                                                            29

Приложение Б                                                                                                            43

Приложение В                                                                                                            44

1 ИСХОДНЫЕ ДАННЫЕ

Рисунок 1 – Принципиальная схема гидросистемы

Таблица 1 - Параметры гидросистемы

Наименование параметра	Обозн.	Номер магистрали
		1	2	3	4	5
Диаметр, м	dтр	0,014	0,015	0,01	0,02	0,015
Длина, м	l	1,5	1	2	0,55	0,5
Толщина стенки трубопровода, м		3*10-4	3*10-4	3*10-4	3*10-4	3*10-4
Коэф-нт местных сопротивлений		5	3	505	2	1.5
Давление потребителя, Па	p	0.1*106	0.15*106	0.19*106	---	---
Рабочая жидкость			Масло веретенное АУ: ; Ес=1,7*108 Па.
Материал трубопровода			Сталь: Етр=2,1*1011 Па
Коэффициент потерь на трение при турбулентном потоке
Номер схемы			10

2 РАЗРАБОТКА динамической модели гидравлической        системы

2.1 Компонентные и топологические уравнения гидросистемы

           В методе сосредоточенных масс, каждый элемент рассматривается простым, т. е. наделенный одним физическим свойством. Состояние простого элемента характеризуется одной фазовой переменной типа потока и одной типа потенциала, математическая модель, выражающая зависимость между этими переменными называется компонентным уравнением. Компонентное уравнение получается, на основе физических законов имеет, следующий вид:

 - для инерционного элемента:

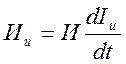
- для диссипативного элемента:

- для упругого элемента:

Для получения полной математической модели необходимо объединить все компоненты уравнения в общую систему уравнения. Объединение осуществляется на основе физических законов, выражающих условие равновесия и непрерывности, уравнение этих законов называют топологическим уравнением, и  они описывают характер взаимодействия между простыми элементами.

- Условие равновесия записываются для фазовых переменных типа потенциала:

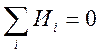
- Условие непрерывности для фазовой переменной типа потока:

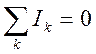
Если фазовая переменная векторной величины, учитывает только топологию, а компонентных уравнениях используются только абсолютные значения.

 В гидравлической системе фазовая переменная типа потока расхода – Q, м³/с, а типа потенциала давление -  р, Па или Н*м².

- Компонентное уравнение инерционного элемента:

получается на основе уравнения Эйлера.

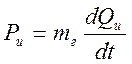
где,m_г – коэффициент массы кг/м⁴.

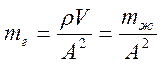
где,  р - плотность;

V – объем жидкости в выделенном участке трубопровода длинной l.

V=A*l

где, А – площадь поперечного сечения трубопровода;

m_ж – масса жидкости в участке трубопровода.

 Инерционные свойства обусловлены затратами давления на разгон жидкости.

- Компонентное уравнение диссипативного элемента:

получается с учетом уравнения Навье – Стокса.

где, коэффициент гидравлического сопротивления .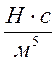

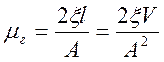
где,  коэффициент для линеаризованного вязкого трения жидкости (по справочнику).

- Компонентное уравнение упругого элемента:

где, с_г – коэффициент гидравлической жесткости Н/м⁵.

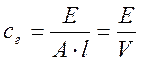
где, Е – модуль объемной упругости жидкости Н/м².

Топологические уравнения.

1 Условие равновесия потенциалов:

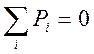
2 Условие непрерывности потоков:

.

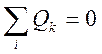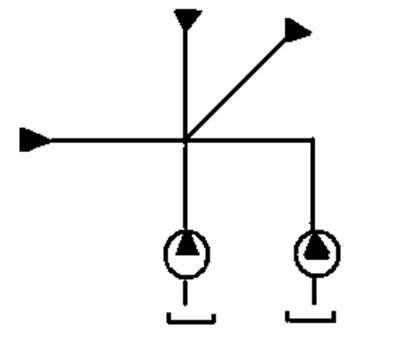
 2.2 Описание гидросистемы и разработка схемы динамической модели

На рисунке 1 приведена принципиальная схема, гидравлической системы, состоящей: из трех гидромагистралей потребителя – 1,4,5; двух насосов – 2,3 и соединительной магистрали – 2,3.

 При построении динамической модели учтем основные свойства гидравлической системы, будем считать магистрали сравнительно короткими и рассматривать их, как дискретные элементы (магистрали), рассматриваем как сосредоточенную, так как длина соединительной магистрали значительно меньше магистрали потребителей, то в первом приближении массой жидкости в ней можно пренебречь.

Внешнее воздействие на гидросистему создаются потребителями и насосами, при чем воздействие потребителей, представляет собой источники потенциалов,  воздействие насосов, источники потока. Источники потенциалов описываются функциями давлений P_i=F(t), характеризующий потери напора в гидроаппарате и потребителя, а источник потока, функция расхода (подача насоса), Q_н=const.

 Упругий элемент, учитывающий сжимаемость в газожидкостной смеси и деформированность стенок трубопровода, подключают в точку ветвления гидравлической магистрали. Он осуществляет дифференциальное соединение всех инерционных элементов и источников потока. На рисунке 2 представлена схема динамической модели гидросистемы.

Рисунок 2 – Схема динамической модели гидросистемы

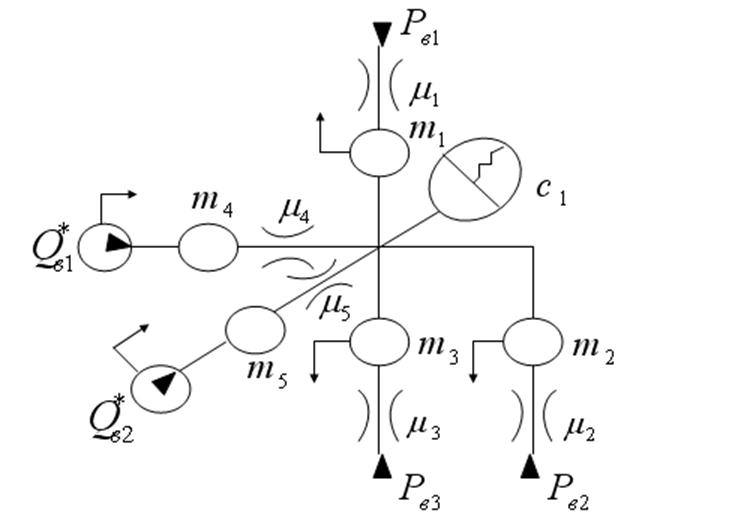
 2.3 Построение орграфа гидросистемы