Расчёт гидравлической системы, состоящей из потребителей выходного расхода с устройства, насосов потока управления и соединяющих магистралей

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Моделирование представляет собой процесс замещения объекта исследования некоторой его моделью и проведение исследования на модели с целью получения необходимой информации об объекте.

Модель – физический или абстрактный образ моделируемого объекта, удобный для проведения исследования и позволяющий адекватно отображать интересующий исследователя физические свойства и характеристики объекта

Различают моделирование предметное и абстрактное. При предметном моделировании строят физическую модель, которая соответствующим образом отображает основные физические свойства и характеристики моделируемого объекта. При этом может иметь иную физическую природу в сравнении с моделируемым объектом. Если модель  и объект  одной и той же физической природы, то моделирование называется физическим. Физическое моделирование сложных  технических систем сопряжено с большими временными и материальными затратами. При проектировании технических объектов используют множество видов математических моделей, которые представляют собой совокупность математических объектов и отношений между ними, адекватно отображающих физические свойства создаваемого технического объекта.

В общем случае уравнение математической модели связывает физические величины, которые характеризуют состояние объекта. Величины, характеризующие состояние технического объекта, процесс его функционирования называют фазовыми переменными (фазовыми координатами). Вектор фазовых переменных задает точку в пространстве, называемую фазовым пространство. Фазовое пространство в отличии от геометрического многомерное. Его размерность определяется количеством используемых фазовых координат. Обычно в уравнениях математических моделей фигурируют не все фазовые переменные, а только часть из них, достаточная для однозначной идентификации состояния объекта. Такие фазовые переменные  называют базисными координатами. Через базисные координаты могут быть вычислены значения всех остальных фазовых переменных.

При  проектировании технических объектов используют множество видов математических моделей в зависимости от уровня иерархии, степени декомпозиции системы, стадии и этапа проектирования на любом уровне иерархии объект представляют в виде некоторой системы, состоящей из элементов.

В зависимости от степени абстрагирования различают три основных иерархических уровня: верхний (метоуровень), средний (макроуровень), нижний (микроуровень).

Метоуровень  соответствует начальным стадиям проектирования. Для построения математической модели метоуровня используют методы математической логики, теории графов и т.п.

На макроуровне объект проектирования рассматривают как динамическую систему с сосредоточенными параметрами. ММ макроуровня представляет собой систему обыкновенных дифференциальных уравнений.

На микроуровне объект представляется как сплошная среда  с распределенными параметрами. Для описания процесса функционирования таких объектов используют дифференциальные уравнения в частных производных. На микроуровне проектируют неделимые по функциональному признаку элементы технической системы, называемые базовыми элементами.

Процесс моделирования включает несколько этапов:

1.  Постановка задачи и определение свойств реального объекта, подлежащего исследованию;

2.  Констатация затруднительности или невозможности исследования реального объекта;

3.  Выбор модели, хорошо описывающая основные свойства объекта с одной стороны и легко поддающиеся исследования с другой;

4.  Исследование модели в соответствие с поставленными целями;

5.  Проверка адекватности модели и объекта;

Если нет соответствия, то необходимо повторить первые четыре пункта.

1  МОДЕЛИРОВАНИЕ НА МИ КРОУРОВНЕ 

1.1   Исходные данные

 Исходные данные для выполнения первой части курсовой работы:

2. Начальные и граничные условия:

Q(x,0)=Q₀(x)                                                                                                           (2)

0≤x≤1        t≥0     a≠0

3. Стандартизирующая функция:

ω(x,t)∞f(x,t)+Q₀(x)δ(t)+a²δ(x)g₁(t)a² δ(L-x)g₂(t)

4. функция Грина: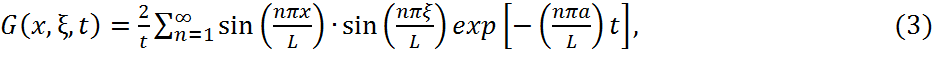

5. Континуальная передаточная функция:

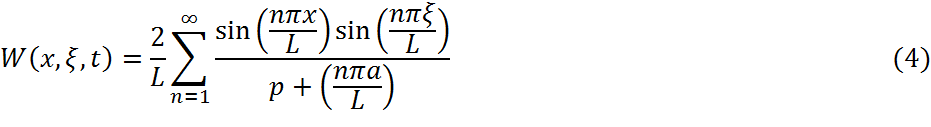
1.2  Идентификация краевой задачи

Уравнения математической физики являются основой для построения математической модели элементов системы уравнения с распределенными параметрами. Для их практического применения основной сложностью является выбор уравнения, которое могло бы заданной точностью и степенью достоверности описать интересующий  элемент системы.

Уравнение (1) представляет собой одномерное уравнение параболического типа, содержащее первую производную по времени t. Данное уравнение описывает нагрев стержня. Проведем идентификацию всех величин входящих в  уравнение (1).

Дифференциальное уравнение имеет вид:

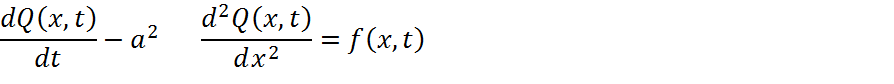
Где Q(x,t)- выходная распространенная величина, представляющая собой изменение температуры стержня, ⁰С;

F(x,t)-входное распространенное воздействие на стержень, м/с²;

Входное воздействие:

f(x,t)=0

Для уравнения (1) формулируется следующие условия:

-начальные условия;

-граничные условия.

Стандартизирующая функция, компенсирующая влияние начальных и граничных условий для данной одномерной задачи имеет вид ().

Функция Грина, являющаяся решением краевой задачи при начальных и граничных условиях и входного воздействия в виде δ- функция имеет вид ()

Континуальная передаточная функция, являющаяся преобразованием Лапласа от функции Грина имеет вид ()

Для того чтобы изменение температуры  Q(x,t) было  однозначно определено в любой точке стержня  и в любой момент времени, необходимо задать граничные условия на концах стержня и начальные условия.

Определим граничные условия на концах

Определим граничные условия на концах стержня .

Г [Q(x,t)]=g₁(t)=273

Г [Q(x,t)]=g₂(t)=10sin(0,006*t)+273

 

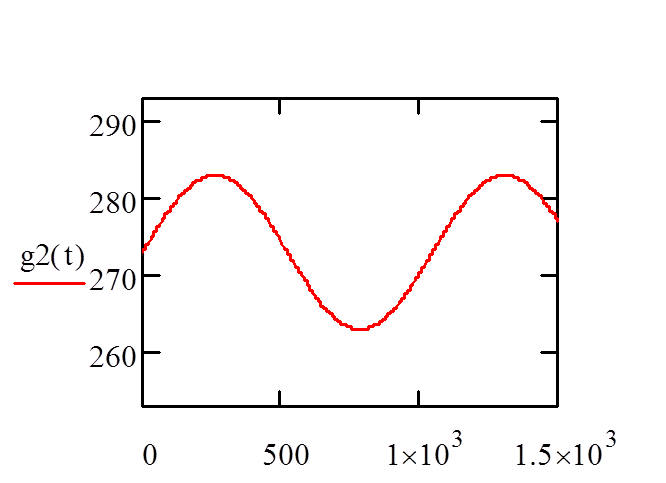
Рисунок 1 – Построение графика зависимости g(t) по заданным параметр

C учетом входного воздействия, принятых начальных и граничных условий стандартизирующая функция примет вид

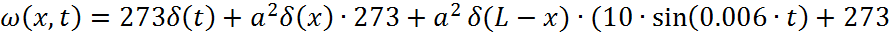
_{1.3. Расчет статической характеристики.}

_{Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная композиция от произведения функции Грина на стандартизирующую функцию:}

 

_{1.3. Расчет статической характеристики.}

_{Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная композиция от произведения функции Грина на стандартизирующую функцию:}

_{…………………………………………………………………………………….}

_{Выходная величина Q(x,t) находится как сумма трех составляющих:}

_Q(x,t)=Q1(x,t)+Q₂(x,t)+Q₃(x,t)

где Q₁(x,t), Q₂(x,t) и Q₃(x,t) находятся как:

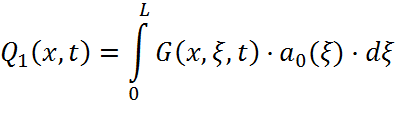
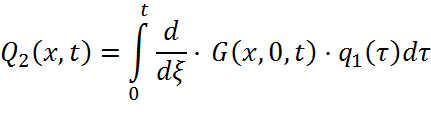
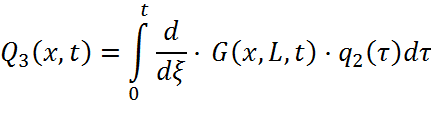
Решим каждый интеграл отдельно:

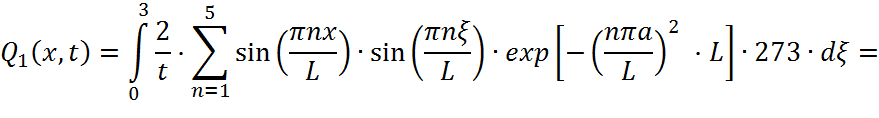
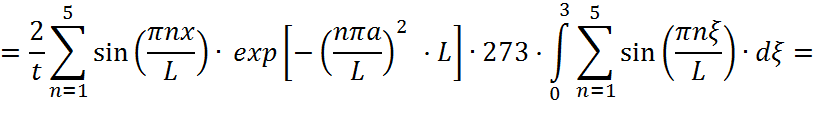
Произведем замену: 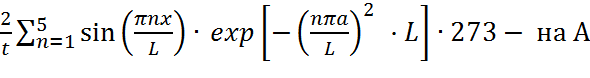 ,  получим:

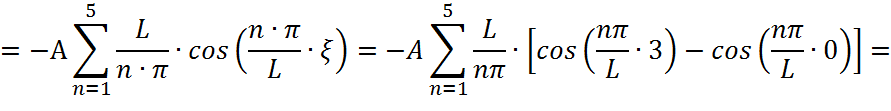
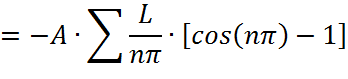
_{Вычислим производную от функции Грина:}

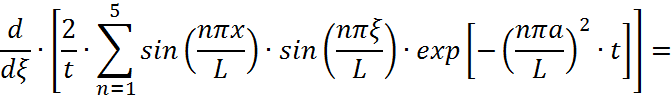
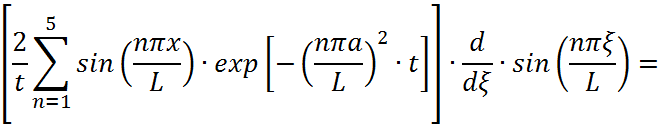
_{произведем замену:}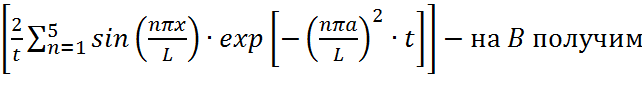

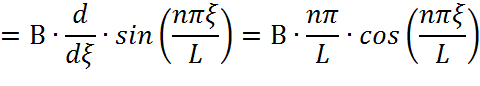
_{Найдем вторую производную:}

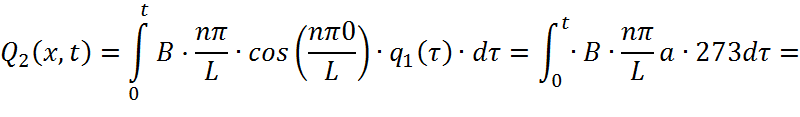
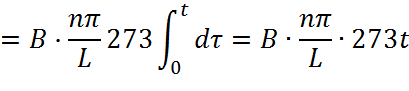
Найдем третью составляющую:

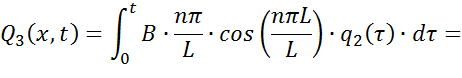
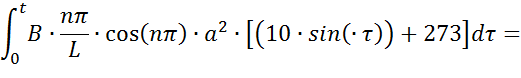
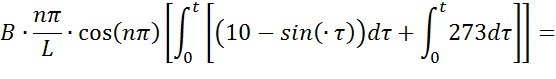
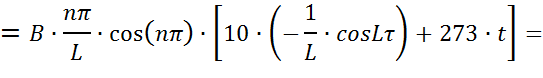
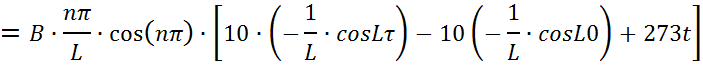
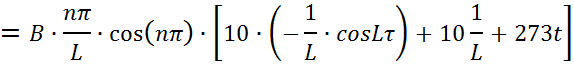
_{Построим график этой функции при фиксированном t:}

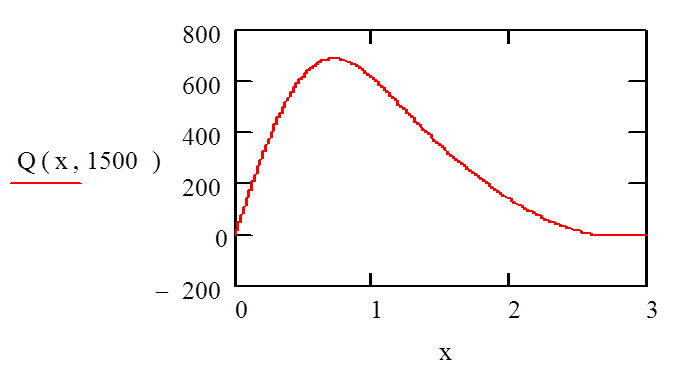
_{Рисунок 2 – Статическая характеристика температуры при t}

 

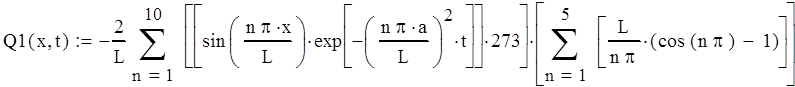
_{Вычислим производную по функции Грина}

 

 

 

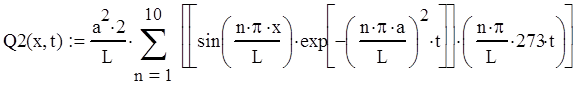
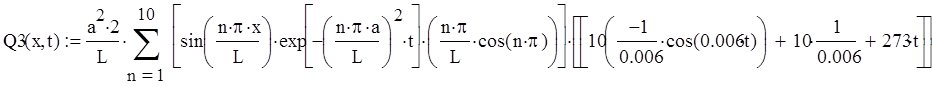
_{1.4 Расчет динамической характеристики}

_{Интегральная передаточная функция рассчитывается как пространственная композиция от произведения континуальной передаточной функции W(x,ξ,p) и от преобразованной по Лапласу стандартизирующей функции ω(x,t) с выделенными из нее входным воздействием.}

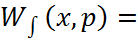
_{Найдем изображение стандартизирующей Функции по Лаплассу:}

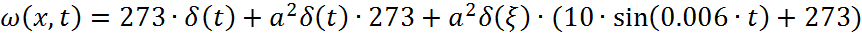
_{Интегральную передаточную функцию представим в виде:}

 

 

 

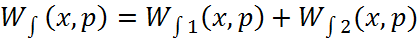
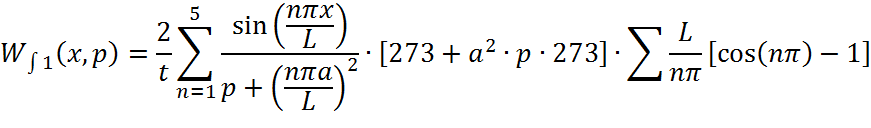
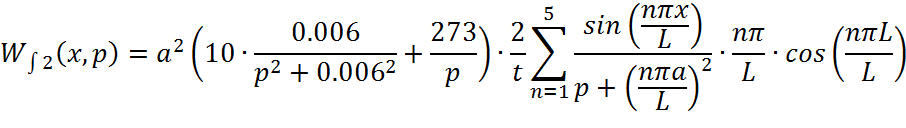
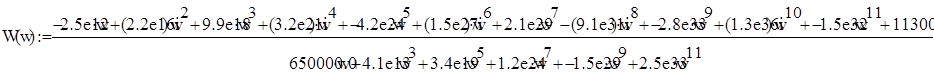
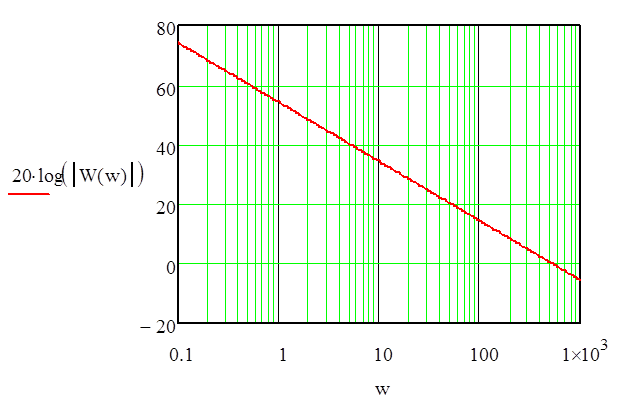
_{Найдем ЛАЧХ по выражению:}

_{Для построения характеристики используем программу MathCAD:}