Расчёт гидравлической системы, состоящей из потребителей выходного расхода с устройства, насосов потока управления и соединяющих магистралей, страница 2

_{Рисунок ,,,- График логарифмической амплитудно- частотной характеристики стержня}

_{Рисунок… - График  аппроксимированной логарифмической амплитудно - частотной характеристики стержня}

_{Аппроксимируя полученную логарифмическую амплитудно- частотную характеристику стандартными наклонами 20 дБ/дек. Тогда передаточная функция будет иметь вид:}

_W(p)=K/P

_{1.5  Моделирование стержня в программе Еlсut}

_{С помощью программы Еlсut можно моделировать задачи магнитостатики и электростатики, электрических и магнитных полей, задачи теплопередачи и упругих деформаций.}

_{Смоделируем нагрев стержня при граничных условиях. Для этого создадим  задачу Еlсut, единицы измерения метры, затем построим плоскую модель стержня- прямоугольник. Зафиксируем левый и правый концы стержня, поскольку его граничное условие равно 0. Зададим входное воздействие. Затем выполняем команду «Решить задачу», результат решения показан на рисунке….}

 

 

 

 

 

 

 

 

 

_{..- Моделирование положения струны от начального положения}

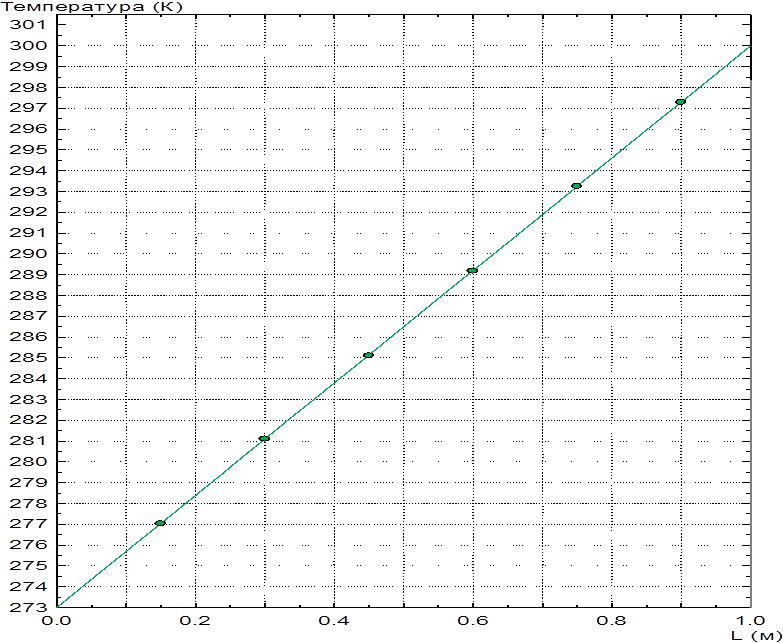
_{График распределения температуры вдоль длины стержня}

_{Пример нахождения  локальных значений:}

_{X=-0.058 м}

_{Y=0.002 м}

_{R=0.058034 м}

_{q=178.03 град}

_{Температура T=284.93 К}

_{Градиент G=27 К/м}

_{Градиент  Gx=-27 К/м}

_{Градиент  Gy=-3.516e-7 К/м}

_{Тепловой поток  F=10530 Вт/м2}

_{Тепловой поток  Fx=-10530  Вт/м2}

_{Тепловой поток Fy=-1.371e-4         Вт/м2}

_{Теплопроводность λ=390 Вт/К•м}

2 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

2.1 Исходные данные

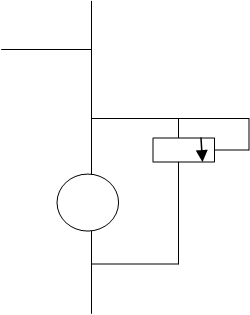
На рисунке 8 приведена расчетная схема гидравлической системы, состоящей из потребителей выходного расхода с устройства 1,2; насосов потока управления 3,4 и соединяющих магистралей.

 

Рисунок 8 – Расчетная схема гидравлической системы

Данные для расчета представлены в таблице 1.

Таблица 1 – Данные для расчета гидравлической системы

Наименование параметра	Обозначение	Номер магистрали      1             2              3
Диаметр, м	dтр	0,02            0,03       0,02
Длина, м	L	1,5               2,05         2
Толщина стенки трубопровода, м*10-3	δтр	2                  2                    2
Коэффициент местных сопротивлений	ξ	4              5,5            5
Давление потребителя Па*106	Р	0,2                    0,2      0,25,0,5
Рабочая жидкость	Масло веретённое АУ ρ=860 кг/м3; υ=0,15*10-4м2/с; Ес=1,7*1010Па
Материал трубопровода	Латунь: Етр=9*1010Па
Коэффициент потерь на трение при турбулентном потоке	Λт=0,028

2.2 Графические формы математической модели

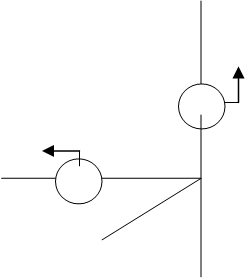
2.2.1 Д и н а м и ч е с к а я  с х е м а  г и д р о с и с т е м ы. При построении модели учтены основные свойства гидравлической системы. Гидравлические магистрали представлены как дискретные элементы, наделенные инерционными и диссипативными свойствами, а масса жидкости в ней- как сосредоточенная. В точках ветвления установлены упругие элементы, учитывающие сжимаемость жидкости и деформируемость трубопровода. Внешние воздействия на систему  представлены в виде источников потенциалов- давления насосов и потребителей. На рисунке 6 представлена динамическая модель гидравлической системы.

 

                                                          

Рисунок      –Динамическая модель гидравлической системы

2.2.2 О р и е н т и р о в а н н ы й   г р а ф. В инженерной практике часто используют графические формы математических моделей, где графическое изображение элементов отождествляется с их компонентными уравнениями, а соединение элементов соответствует топологическим уравнениям.

Графическая  модель может быть представлена в виде графа или эквивалентных схем. Граф представляет структурную математическую модель системы и отображает ее топологию.

Эквивалентная схема представляет функциональную модель и отображает как топологию, так и компонентный состав.

Ветви графа и эквивалентной схемы соответствуют компонентам математической модели. Они отображают математическое описание инерционных элементов и источников внешних воздействий. При этом эквивалентной схемы используются стандартные обозначения. Ветвям графа дают обозначения параметров отождествляемых ими элементов или обозначение источников внешних воздействий.

Узлы графа и эквивалентной схемы соответствуют узлам дискретизации непрерывных объектов, которые совпадают с сосредоточенными массами. Один из узлов графа или схемы отображает инерционную систему отсчета фазовых координат типа потока и имеет название базового узла или базы и ему присваивают нулевой номер. Остальные узлы нумеруются согласно принятым обозначениям сосредоточенных масс.

Если обозначить направление сигналов в ветвях графа или орграфа, в ветвях источников внешних воздействий системы – направлены от базы к узлу, если энергия подводится к узлу и источник обеспечивает возрастание потоковой переменной узла. При отводе энергии от узла – направление от узла к базе.