Расчёт гидравлической системы, состоящей из потребителей выходного расхода с устройства, насосов потока управления и соединяющих магистралей, страница 4

Расчет произведен с помощью Mathcad  и представлен в приложении.

В таблице представлены результаты при двух значениях подачи насоса

Таблица 4 – Результаты статического анализа

Фазовые координаты	Рн=0,25*106Па	Рн=0,5*106Па
Q1,м3/с	1,529*10-7	9,173*10-7
Q2,м3/с	1,234*10-7	7,405*10-7
Q3,м3/с	2,764*10-7	1,658*10-6
Ру1,Па	2,055*105	2,33*105

2.5 Анализ динамической системы

Характеристики функционирования технических систем определяются ее внутренними физическими свойствами и внешними воздействиями, которые подразделяются на возмущающие и управляющие. Для гидравлической системы возмущающим воздействием является давление потребителя, а управляющим – подача насосов. Для технической системы наиболее характерно функционирование в условиях непрерывно изменяющихся внешних воздействий, при которых состояние систем характеризуется  изменением во времени фазовых координат системы. Такой режим работы системы называется динамическим. Основным показателем динамической системы является переходный процесс, моделирование которого позволяет исследовать быстродействие, точность, колебательность и другие свойства технической системы.

Решение задачи переходного процесса происходит в 3 этапа:

-интегрирование системы дифференциальных уравнений;

-определение показателей качества;

-оценка степени выполнения технических требований проектируемой технической системы.

В общем случае система дифференциальных уравнений имеет вид:

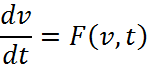
где  А-матрица Якоби;

v- вектор фазовых координат;

U- вектор функции внешних воздействий.

С учетом произведенных ранее расчетов запишем систему дифференциальных уравнений, представляющую динамическую гидросистемы:

Переходный процесс определяется в результате числительного интегрирования системы, для чего необходимо произвести выбор ряда параметров.

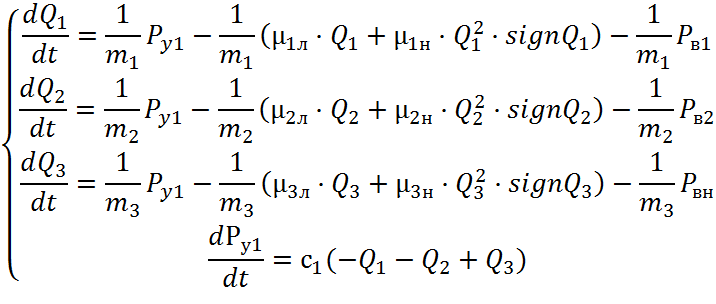
Так как система дифференциальных уравнений нелинейная, то элементами матрицами Якоби являются частные производные по фазовым координатам:

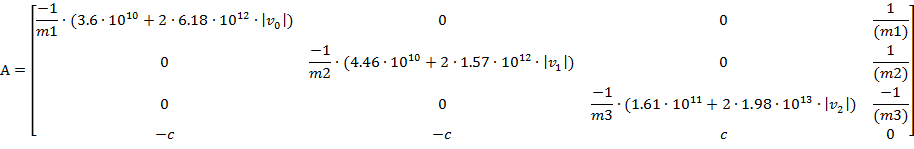
Переходную характеристику определяют в результате численного интегрирования системы дифференциальных уравнений, для чего необходимо провести выбор ряда параметров. Пусть переходный процесс оценивается как реакция системы, находящийся в состоянии покоя на ступенчатое воздействие вида:

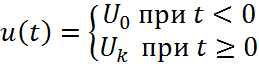
где и – начальное и конечное значение функции воздействия U(t), причем   и – const, (U₀≠U_k).

В нашем случае таких внешних воздействий как давление потребителей остаются неизменными, а ступенчатое воздействие организуется отключение насоса:

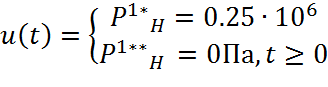
Начальное и конечные значения всех фазовых координат определены при анализе статического состояния системы:

                      

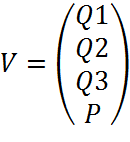
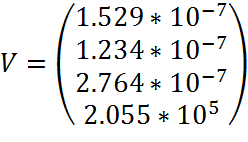
Если система устойчива, то через некоторый промежуток времени система придет из состояния v₁ в состояние v₂. Для числительного интегрирования будет использоваться неявный метод Эйлера. Вектор входных воздействий при    имеет вид:

Для устойчивости численного метода необходимо корректно выбрать шаг интегрирования h, исходя из условий устойчивости, котjрое для метода Эйлера имеет вид:

где λ – собственное значение матрицы Якоби.

Для комплексного значения условие имеет вид:

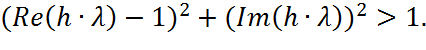
Собственными  значениями матрицы Якоби порядка n называют корни λ_к, k=1,n его характеристического уравнения, определяющего по формуле:

Где Е – единичная матрица.

Произведем расчет значений матрицы Якоби с учетом начальных значений расхода:

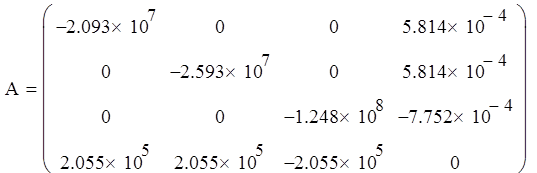
Тогда характеристическое уравнение имеет вид:

Вычислив корни характеристического уравнения, найдем собственные значения матрицы Якоби:

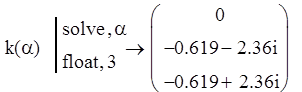
Корни характеристического уравнения имеют как отрицательные значения действительных частей, что говорит об устойчивости системы.

Рекомендуемый шаг h=0,5с.Выполним проверку устойчивости численного метода Эйлера при данном шаге:

Следовательно, шагh=0,5 обеспечивает устойчивость метода, то есть приемлемую точность вычислений.

Применим численный метод Эйлера для решения системы дифференциальных уравнений данной работы.

Формула численного интегрирования, неявного метода Эйлера имеет вид:

 – определяется из исходной системы дифференциальных уравнений

Совместное преобразование последних двух выражений приходит к следующей зависимости:

где, А= модифицированная матрица Якоби, на к+1 шаге пересчитывается исходя из элементов катого шага по формуле:

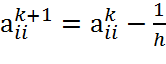
А остальные элементы не изменяются.

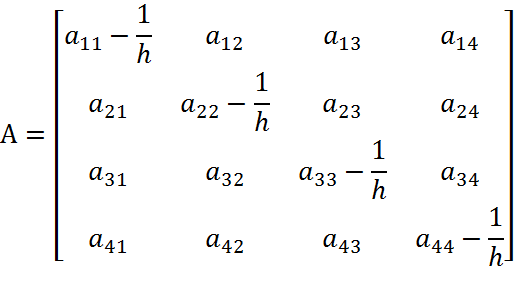
B- модифицированный вектор входных воздействий, на k+1 шаге, определяется по формулам:

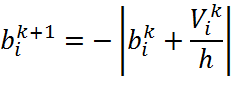
Решение системы уравнений А*V_k+1=B, дает значение фазовых координат на k+1 шаге, то есть  в момент времени t_k+1.

Алгоритм неявного метода Эйлера с постоянным шагом h:

1)  Задание шага интегрирования h.

2)  Задание начальных значений V₀ при t₀=0.

3)  Вычисление времени 

4)  Вычисление матрицы А и В на к+1 шаге.

5)  Решение системы уравнений А* V_k+1=В, с целью определения V_k+1  на временном участке t_k+1.

Получили:

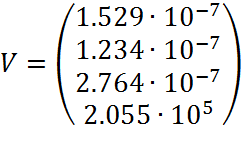
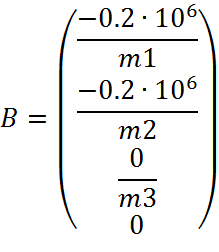
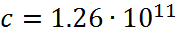
Рисунок .. – Переходный процесс системы

По графикам .. и .., видно, что при внешних воздействий на гидросистему, происходит переходный процесс, при котором система переходит из одного установившегося в другом. Это говорит о том, что данная система устойчива.