Расчёт гидравлической системы, состоящей из потребителей выходного расхода с устройства, насосов потока управления и соединяющих магистралей, страница 3

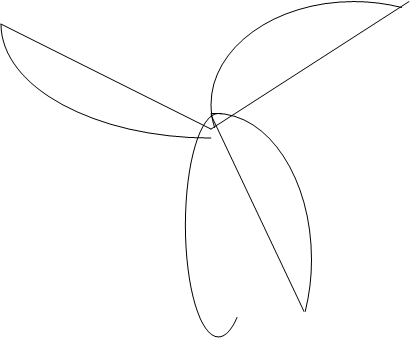
Ветви инерционных элементов всегда имеют направление от узла к базе, в ветвях упругих элементов стрелки указывают направление передачи энергии от источника к потребителю. Ветви диссипативных компонентов могут быть параллельны как инерционным, так и упругим элементам и направления в них совпадают.

На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы и представленный на рисунке……..

Ветви упругих элементов расставлены от насосов к потребителям

 

2.2.3 М а т р и ц а  и н ц и д е н т н о с т и. Информация о математической  модели технического объекта, которую содержит орграф, может быть представлена в виде матрицы. Матрица имеет размерность [а/р], где а – число строк, соответствующих узлам орграфа, за исключением базовых,  р - число столбцов, соответствующее ветвям орграфа. Единицами отмечается наличие соединений между узлами и ветвями, а 0 – их отсутствие. Направление сигналов в ветвях отображается знаками 1 : (-) – сигнал направлен от узла, (+) – к узлу. Сформированная таким образом матрица носит название матрицы инцидентности.

На основании орграфа сформируем матрицу инцидентности.

Таблица… - Матрица инцидентности гидравлической системы

Узлы	Диссипативные			Упругие	Внешнее воздействие
1	-1	0	0	1	-1	0	0
2	0	-1	0	1	0	-1	0
3	0	0	-1	-1	0	0	1

2,3 Узловой метод формирования математической модели

На основании матрицы инцидентности запишем матрицы параметров инерционных, упругих и диссипативных элементов гидравлической системы:

           

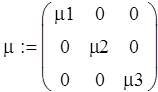
Запишем матрицу потенциалов источников Р_В, упругих Р_У и диссипативных Р_Д элементов и матрицу фазовых переменных типа Q:

                          

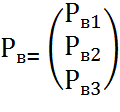
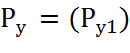
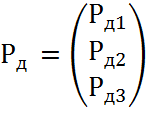
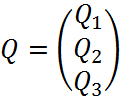
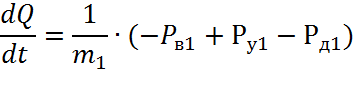
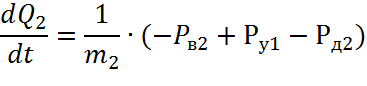
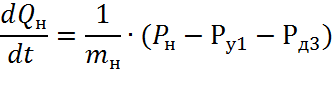
Вычислим матричное произведение слагаемых правой части уравнения

              

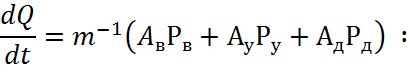
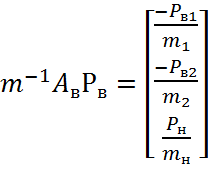
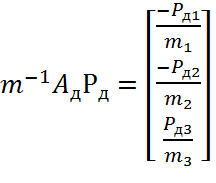
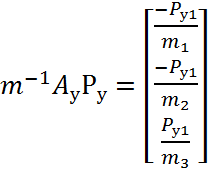
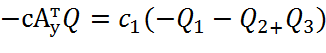
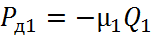
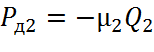
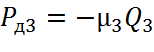
Сложим полученные матрицы в соответствии с уравнением () и учитывая зависимость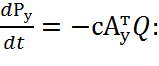

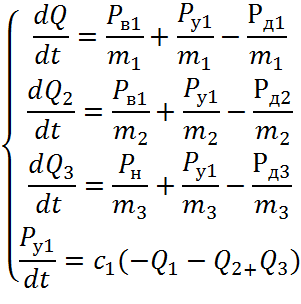
На основании формулы Рд=-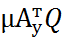 давление диссипативных элементов:

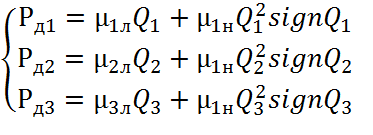
Определим параметры элементов модели, результаты приведены в таблице …….

Таблица ….- Результаты расчета элементов модели

Название	Формула	Магистраль
		1	2	3
Площадь сечения трубопровода,		3,14	7,07	3,14
Объем трубопровода,		4,71	1,77	6,28
Доля объема трубопровода		0,164	0,616	0,219
Коэффициент массы		9,51	7,08	3,18
Коэффициент линейный гидр. потерь		3,6	4,46	0,16
Коэффициент нелинейный гидр. потерь	+	6,18	1,57	0,198
Коэффициент жесткости участка		2,16	0,151	1,21
Коэффициент жесткости элемента		1,26

2.4 Анализ статической системы

2.4.1 Р а з р а б о т к а   с т а т и ч е с к о й   м о д е л и  г и д р о с и с т е м ы

При постоянном воздействии система находится в установленном равновесном состоянии. Ее фазовые координаты расхода магистрали давления точки. Фазовая координата постоянная. Такой режим функционирования системы называется статическим и достигается при постоянных внешних воздействиях.

Так как фазовая координата в данном режиме постоянна, то их производная по времени t равна 0.

Тогда модель гидравлической системы упрощается и принимает вид:

      

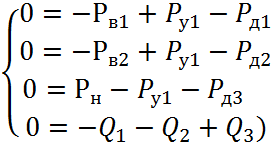
С учетом выражения для диссипативных элементов система преобразуется к виду:

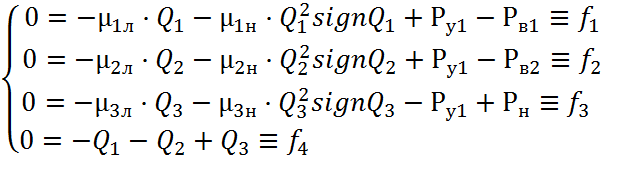
2.4.2  Ф о р м и р о в а н и е   м а т р и ц ы  Я к о б и  в статической модели гидросистемы. Данная система является статической моделью гидросистемы и представляет собой систему алгебраических уравнений.

Для ее  решения используется числительный метод Ньютона.

Предварительно запишем матрицу Якоби, отражающую важнейшие свойства физической системы.

Элемент для матрицы Якоби является частная  производная от нелинейной вектор функции F(V)=(f₁;f₂;f₃;f₄)

По фазовым координатам системы V=(Q₁;Q₂;Q₃;P_у1)

В системе уравнений нелинейной является функция Р_дi=f(Q_i), для которых частные производные имеют вид:

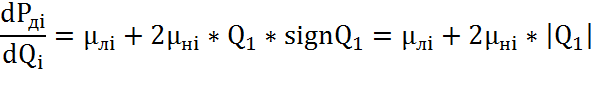
Матрица Якоби составляется следующим образом:

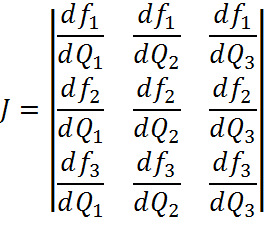
Матрица Якоби исходной системы будет иметь вид:

Тогда  матрица Якоби исследуемой гидросистемы примет вид:

2.4.3 Решение систем уравнения статической модели методом Ньютона. Для решения системы уравнения статической модели использует метод Ньютона. Данный метод обладает наибольшей скоростью сходимости.

Алгоритм метода Ньютона включает следующие этапы.

1)  Выбор начального приближения :

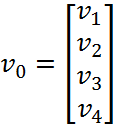
2)  Вычисление матрицы Якоби в точке,(k=0,1,2…).

3)  Вычисление вектора невязок 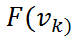 исходной системы алгебраических уравнений:

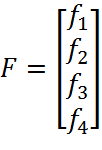
4)  Определение вектора поправок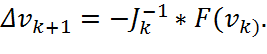

5)  Определение нового приближения вектора искомых фазовых переменных