Разработка динамической модели гидравлической системы. Моделирование и анализ статического состояния гидросистемы, страница 5

4.3 Решение системы дифференциального уравнения методом Эйлера

Формула численного интегрирования, неявного метода Эйлера имеет вид:

 - определяется из исходной системы дифференциальных уравнений

Совместное преобразование последних двух выражений приводит к следующей зависимости:

где, модифицированная матрица Якоби, на к+1 шаге пересчитывается исходя из элементов катого шага по формуле:

,

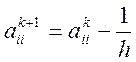а стальные элементы не изменяются.

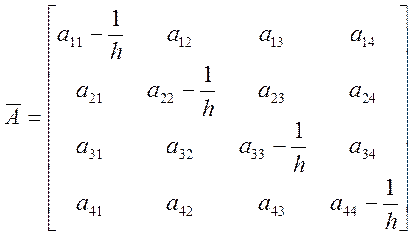
это модифицированный вектор входных воздействий, на к+1 шаге, определяется по формулам:

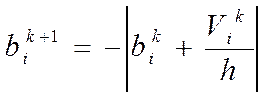
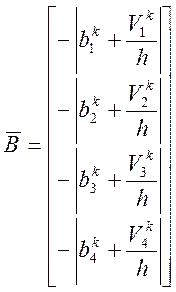
Решение системы уравнений , дает значение фазовых координат на к+1 шаге, то есть в момент времени t_k+1.

Алгоритм неявного метода Эйлера с постоянным шагом h:

1)  Задание шага интегрирование h.

2)  Задание начальных значений  при .

3)  Вычисление времени .

4)  Вычисление матрицы  и  на к+1шаге.

5)  Решение системы уравнений , с целью определения  на временном участке t_k+1.

Получили:

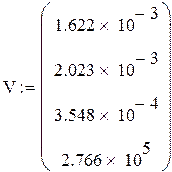
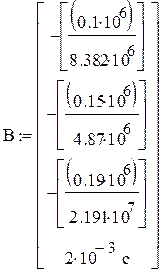
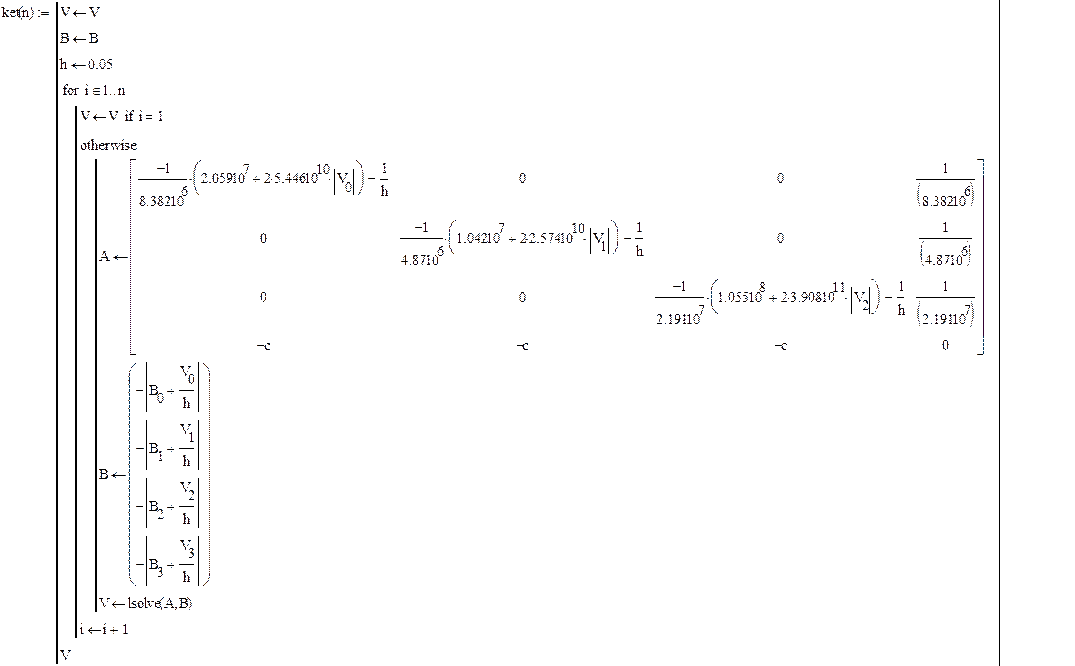
4.4 Определение показателей качества переходного процесса

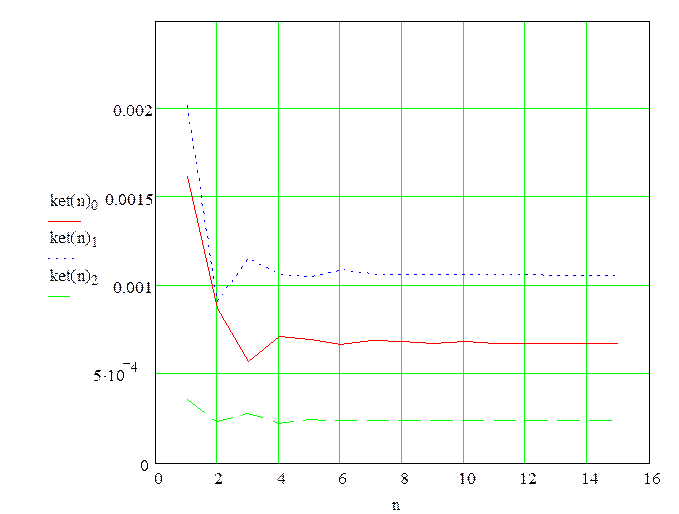
                Рисунок 4 – Показатели качества устойчивости системы

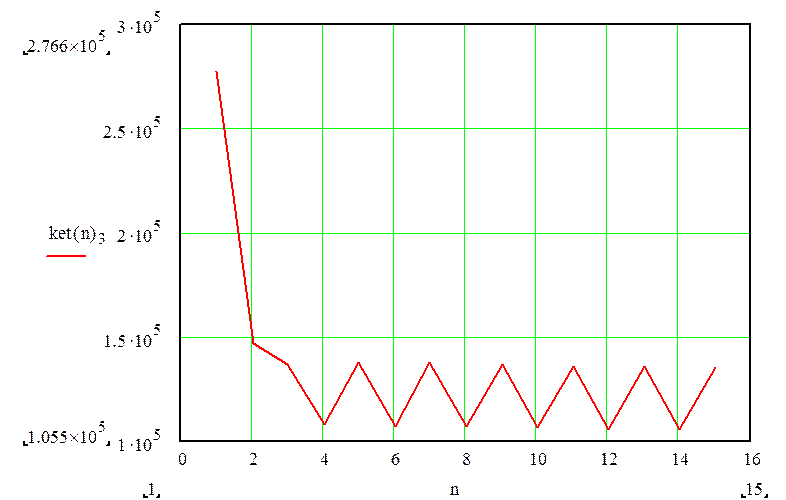
                             Рисунок 5 – Переходный процесс системы

По графикам 4 и 5, видно, что при внешних воздействиях на гидросистему, происходит переходный процесс, при котором система переходит из одного установившегося состояния в другое. Это говорит о том, что данная система устойчива.  

 ПРИЛОЖЕНИЕ А

Результаты статического анализа при

Начальные значения:

0 шаг

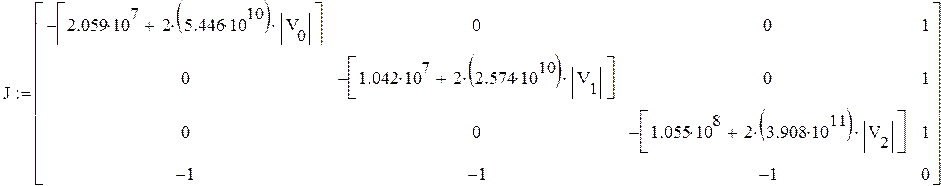
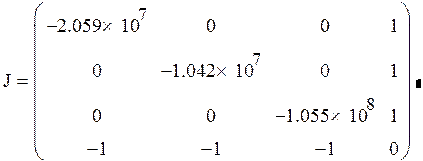
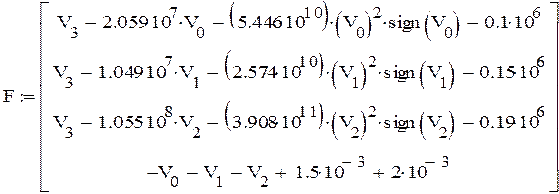
2 шаг

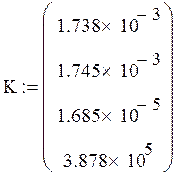
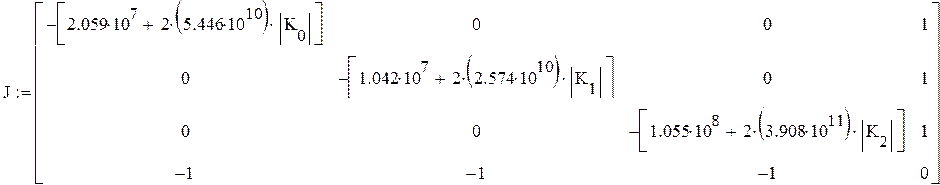
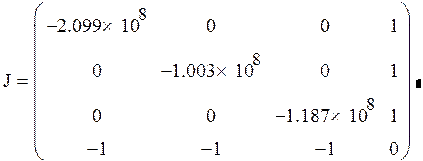
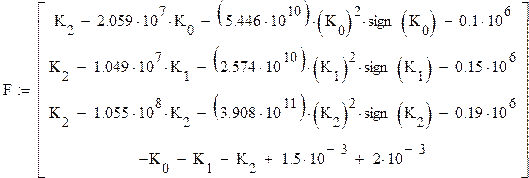
5 шаг

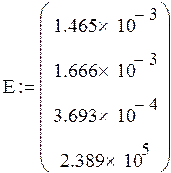
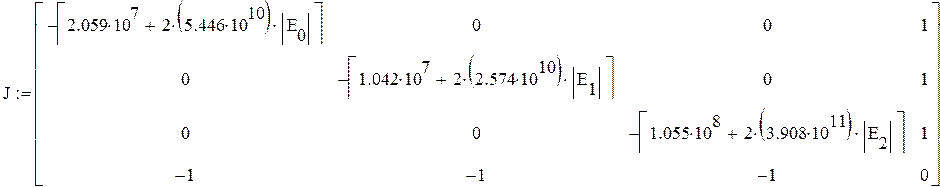
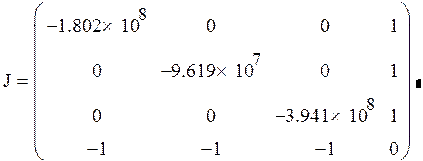
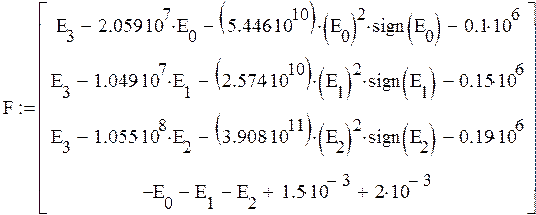
6 шаг

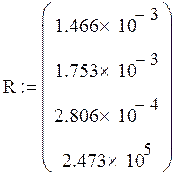
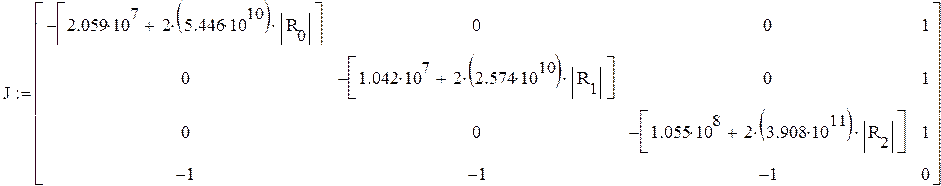
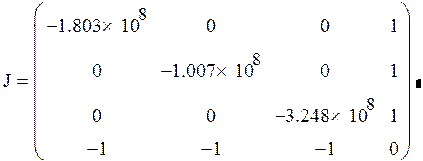
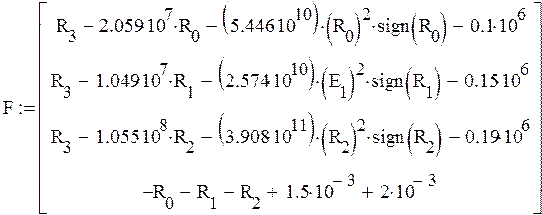
8 шаг

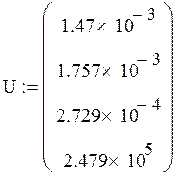
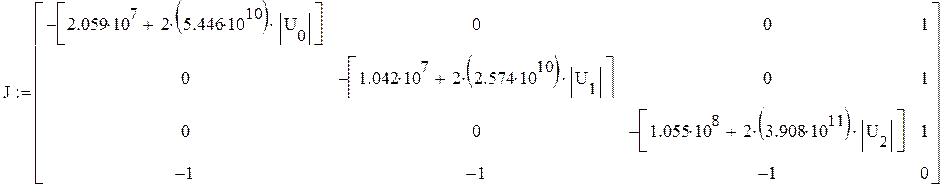
10 шаг

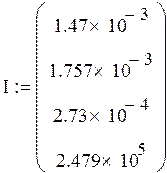
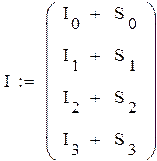
Результаты статического анализа при

Начальные значения:

                    

0 шаг

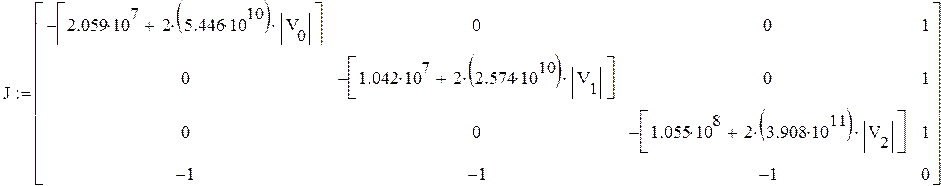
2 шаг

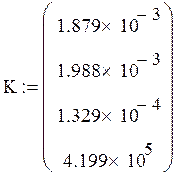
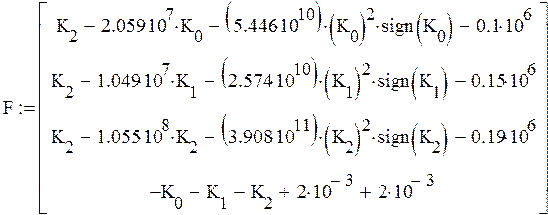
6 шаг

8 шаг

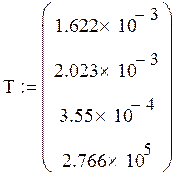
10 шаг

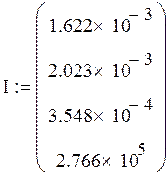
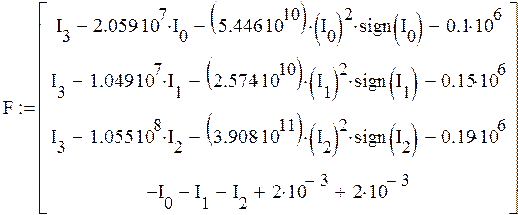
ПРИЛОЖЕНИЕ Б

ПРИЛОЖЕНИЕ В

Метод Эйлера.

Заданные значения: