Орграф (ориентированный граф), позволяет идентефецировать структуру и физическое свойство моделируемой гидросистемы и представляющей собой ее математическую модель в графической форме. Узлы орграфа соответствуют сосредоточенным массам. В нашем случаи это пять гидравлических масс, магистрали потребители – 1,2,3,4,5 и внешние источники потока, насосы – 1*,2*.
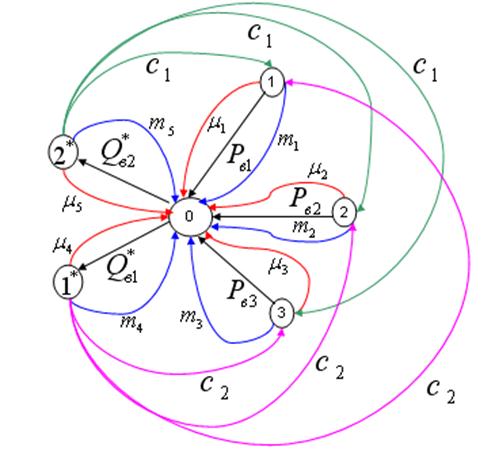
Рисунок 3 – Орграф гидросистемы
Так же на орграфе отмечается, базовый узел с нулевым номером отображения системы отсчета фазовых координат типа потока. Ветви графа отображают описание: инерционных, диссипативных, упругих элементов моделей и источников внешних воздействий.
- В ветвях источников внешних воздействий выберем следующие направления:
а) от базы к 1* и 2* так как расход насоса отдается гидросистеме.
в) от 1,2,3 к базе, так как потребители забирают рабочую жидкость из системы. Всегда ветвь источника соединяет узлы с базой.
- Инерционные ветви соединяют узлы, отождествляющие сосредоточенные массы с базой, направление всегда от узла к базе.
- Ветви упругих и диссипативных компонентов, соединяют между собой взаимодействующие узлы. В соответствии со схемой модели, в нашем случаи ветви диссипативных элементов соединяют узлы с базой так как база соответствует точки ветвления гидросистемы, при таком соединении направление от узла к базе.
- В ветвях упругих компонентов, направление передачи энергии от источников – 1* и 2*, к потребителям – 1,2,3.
2.4 Составление матрицы инциденций
Информация о математической модели гидросистемы, которую содержит орграф, представим в виде матрицы инцидентности. Сформированную по следующему правилу.
1 Размерность матрицы:
а) число строк соответствует каждому узлу орграфа. За исключением базы – 4 и 5;
в) число столбцов соответствует ветвям орграфа – 17+1.
2 Элементы матрицы:
а) отсутствие связи между узлом и ветвью – «0»;
в) если ветвь входит в узел – «1»;
г) если ветвь выходит из узла – «-1»;
Источник потока ![]() , формально заменяется на источник
потенциала
, формально заменяется на источник
потенциала ![]() и добавляется условная масса
и добавляется условная масса ![]() - «+1».
- «+1».
Таблица 2 – Матрица инцидентности.
|
Узел |
Ветви |
|||||||||||||||
|
инерционные |
диссипативные |
упр. |
Источники потенциалов |
|||||||||||||
|
m1 |
m2 |
m3 |
m4 |
m5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
+1 |
-1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
+1 |
0 |
-1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
+1 |
0 |
0 |
-1 |
0 |
0 |
|
1* |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
|
2* |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
|
подматрица |
Аи |
Ад |
Ау |
Ав |
||||||||||||
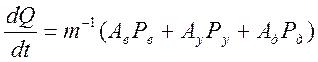 (1)
(1)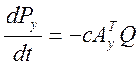 (2)
(2)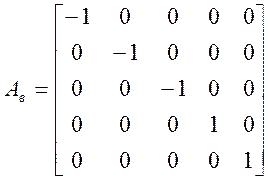 ,
, 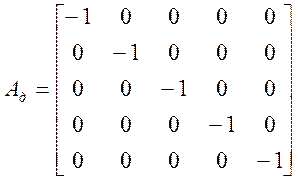 ,
,
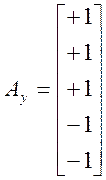 .
.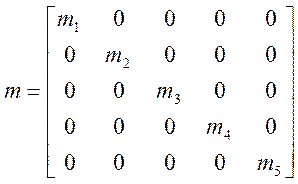 ,
, 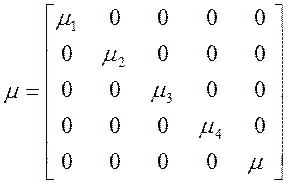 .
.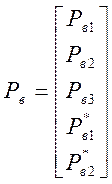 ,
,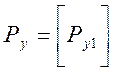 ,
, 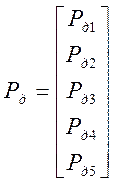 .
.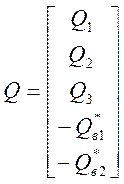
Вычислим матричное произведение слагаемых правой части уравнения (1):
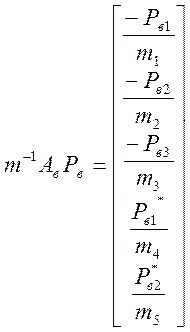 ,
, 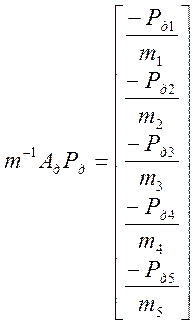 ,
, 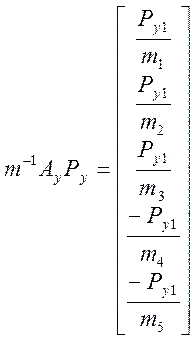 .
.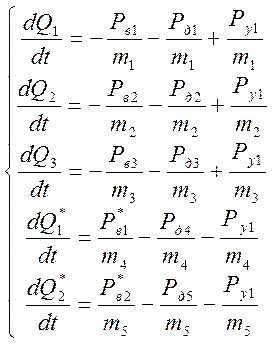
(4)
(5)
(6)
Учитывая, что ![]() ,
тогда
,
тогда ![]() , тогда вместо двух последних уравнений
системы, имеем:
, тогда вместо двух последних уравнений
системы, имеем:
![]()
![]() (7)
(7)
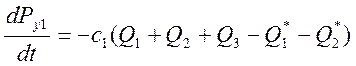 (9)
(9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.