![]() (10)
(10)
![]()
![]()
![]()
![]()
Таким образом, математическая модель рассматриваемой гидросистемы, представляется системой, обыкновенных дифференциальных уравнений - (4),(5),(6),(9) и семью алгебраическими выражениями – (7),(8),(10) – (14).
Комплексные уравнения, диссипативных элементов носят более сложный характер, при этом выделяют линейные и нелинейные потери давления в гидромагистралях и уравнения (10) – (14), запишется в следующем виде:
![]() (15)
(15)
где, ![]() коэффициент гидравлического
сопротивления, характеризующий линейные потери при ламинарном режиме движения
жидкости;
коэффициент гидравлического
сопротивления, характеризующий линейные потери при ламинарном режиме движения
жидкости;
![]() коэффициент
гидравлического сопротивления, характеризующий нелинейные потери при
турбулентном режиме, по длине и местные.
коэффициент
гидравлического сопротивления, характеризующий нелинейные потери при
турбулентном режиме, по длине и местные.

2.6 Определение параметров элементов модели
Таблица 3 – Расчет параметров гидросистемы.
|
Параметры |
Формула |
МАГИСТРАЛЬ |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
1) Площадь сечения магистрали |
|
1.539*10-4 |
1.766*10-4 |
7.85*10-5 |
3.14*10-4 |
1.766*10-4 |
|
2) Объем участка трубопровода |
|
2.309*10-4 |
1.766*10-4 |
1.57*10-4 |
1.727*10-4 |
8.83*10-5 |
|
3) Доля объема |
|
0.28 |
0.214 |
0.19 |
0.209 |
0.107 |
|
4) Коэффициент массы |
|
8.382*106 |
4.87*106 |
2.191*107 |
1.506*106 |
2.435*106 |
|
5) Коэффициент линейных гидравлических потерь |
|
2.059*107 |
1.042*107 |
1.055*108 |
1.813*106 |
5.212*106 |
|
6) Коэффициент нелинейных потерь |
|
5.446*1010 |
2.574*1010 |
3.908*1011 |
3.358*109 |
1.287*1010 |
|
7) Коэффициент жесткости участка |
|
2.534*1012 |
4.323*1012 |
5.549*1012 |
4.469*1012 |
1.727*1013 |
Общий коэффициент жесткости при разветвлении трубопровода, находится по формуле:
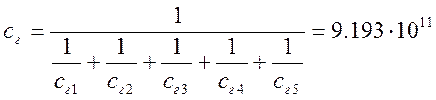
2.7 Использование структурно – матричного метода, формирование математической модели
На основании структурно – матричного метода, уравнение математической модели гидравлической системы, записывается исходя из следующих выражений:
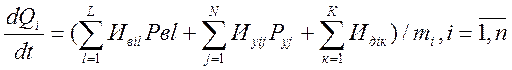 (20)
(20)
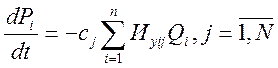 (21)
(21)
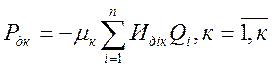 (22)
(22)
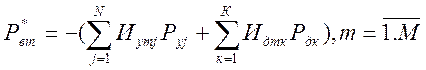 (23)
(23)
где, ![]() количество источников внешних
воздействий типа потенциала;
количество источников внешних
воздействий типа потенциала;
![]() количество
упругих элементов;
количество
упругих элементов;
![]() количество
диссипативных элементов;
количество
диссипативных элементов;
![]() количество
сосредоточенных масс;
количество
сосредоточенных масс;
![]() количество
источников внешних воздействий типа потока.
количество
источников внешних воздействий типа потока.
Для уравнения (20) и (23), суммируем по строкам матрицу инцидентности, а для уравнения (21),(22) по столбцам. В уравнении (21),(22),(23) домножим на
(-1), в итоге имеем:
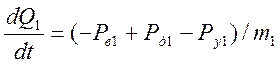
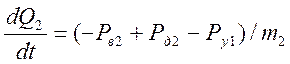
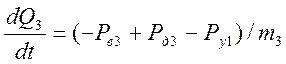
Теперь для (21), запишем в общем виде одно уравнение:
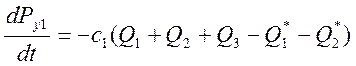
Для уравнения (22), запишем пять уравнений, к=5:
![]()
![]()
![]()
![]()
![]()
Для уравнения (23), получим:
![]()
![]()
В результате расчета,полученное выражение, математической модели, по данному методу идентичны математической модели, сформированной по узловому методу.
3 Моделирование и анализ статического состояния гидросистемы
3.1 Разработка статической модели гидросистемы
При постоянных воздействиях, система находится в установившимся состоянии ее фазовые координаты при этом постоянны, такой режим функционирования системы называют статическим. Статическое состояние гидросистемы достигается при постоянных внешних воздействиях:
1 Подача насоса ![]() .
.
2 Давления в потребителях ![]() .
.
При этом установившиеся постоянные значения, фазовых систем координаты:
1 Расхода жидкости в гидромагистралях
![]() .
.
2 Давление в упругом элементе ![]() , полагая, что
, полагая, что 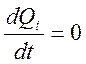 и
и 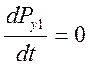 .
.
![]()
Получим следующую систему нелинейных алгебраических уравнений:
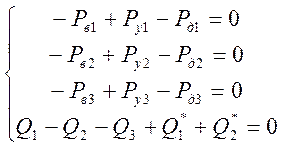 (24)
(24)
С учетом уравнения (15), преобразуем систему к следующему виду:
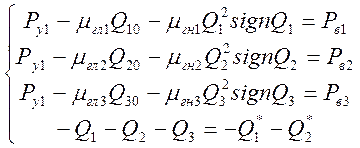 (25)
(25)
Система уравнений (25), является статической моделью гидросистемы, где в правой части уравнений известно значение входных значений. Для ее решения, используют различные численные методы, для которых необходимо предварительно составить матрицу Якоби.
3.2 Формирование матрицы Якоби в статической модели гидросистемы
Матрица Якоби
характеризует важнейшие свойства физической системы, а так же свойства
уравнений математической модели, модель статического состояния гидросистемы,
представляет собой систему нелинейных алгебраических уравнений вида: ![]() . Элементами матрицы Якоби в этом
случаи, являются частные производные от нелинейной вектор функции
. Элементами матрицы Якоби в этом
случаи, являются частные производные от нелинейной вектор функции 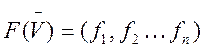 по фазовым коэффициентам системы
по фазовым коэффициентам системы ![]() . Для системы
. Для системы ![]() -
того порядка матрица Якоби имеет вид:
-
того порядка матрица Якоби имеет вид:
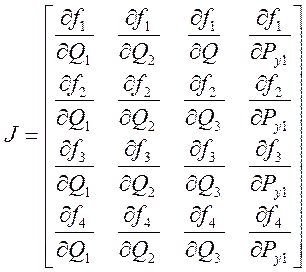 (26)
(26)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.