Расчет интегральной передаточной функции. Преобразование Лапласа от интегральной передаточной функции. Построение частотных характеристик

Выберем дифференциальное уравнение, имеющее вид уравнения в декартовых координатах:

.

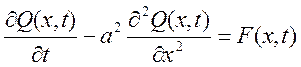         Начальные условия: Q(x,0)=Q₀(x),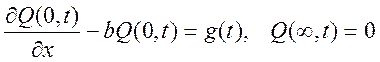

Граничные условия: 0 ≤ x < ∞; t ≥ 0; a² ≠ 0; b ≥ 0.

Нормирующая функция:

Континуальная передаточная функция:

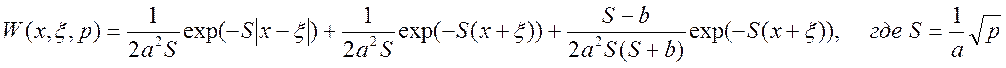
Функция Грина:

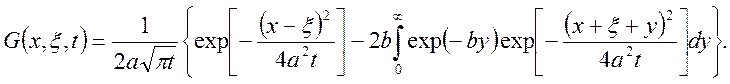
Выверим размерность. На входе действует давление (Па), на выходе получаем перемещение (м).

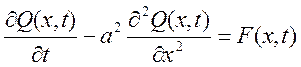
                                                     м/с     а²(м²/с)∙1/м   Па

Где а² (м²/с) –скорость изменение величины площади давления в единицу времени.

Необходимо определить такой коэффициент j, с помощью которого можно провести преобразование размерности входной величины (Па) в размерность выходной (м).

м/с =j Па;   j= м/(Па*с) = (м²*м)/(Н*с) = м³/р,  где р – импульс.

Полученная размерность показывает величину приращения объема при импульсном входном воздействии хода поршня.

Расчет функции поверхности

Зададим начальные, граничные условия и входное воздействие.

Q(x,0) = 0, Q(∞,t) = 0; g(t) = sin(7t); F(x,t) = e^3t

Нормирующая функция запишется в виде:

ω(x,t) = e^3t + a²δ^’(x)sin(7t); δ^’(x) = δ(x)/x; ω(x,t) = e^3t + a² (δ(x)/x) sin(7t)

Вычислим интеграл, представляющий собой основное соотношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями по формуле:

;

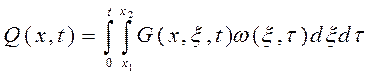Для упрощения вычисления интеграла предварительно разложим все показательные функции вида е^х в ряд Маклорена. Получим:

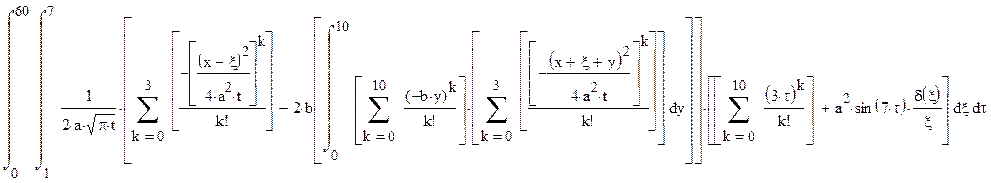
Результат вычисления интеграла (при а = 3, b = 3) представлен в виде дроби, в знаменателе которого находится переменная времени t. Вследствие этого пакет программы MatchCad выдает ошибки «деление на ноль» и «функция поверхности должна быть рациональной». Первую ошибку мы устраняем следующим образом:

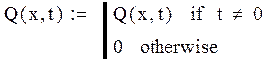
Вторую ошибку исключаем заменой степени переменной знаменателя на «4», (так как степень 7/2 = 3,5, то есть можно приближенно записать как «4»). Получаем следующее выражение:

          Построим функции поверхности при фиксированных значениях постоянных коэффициентов a и b:

При а = 3, b = 3.

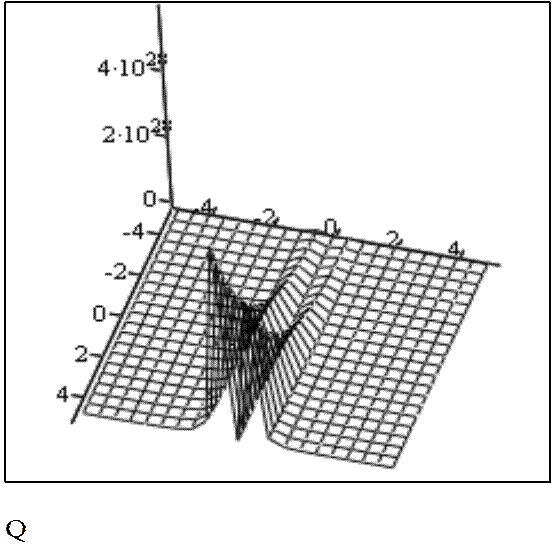
При а = 10, b = 13.

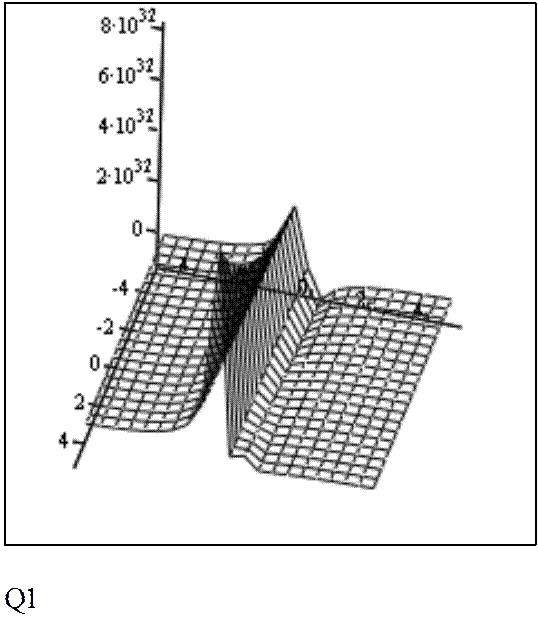
При а = 30, b = 30.

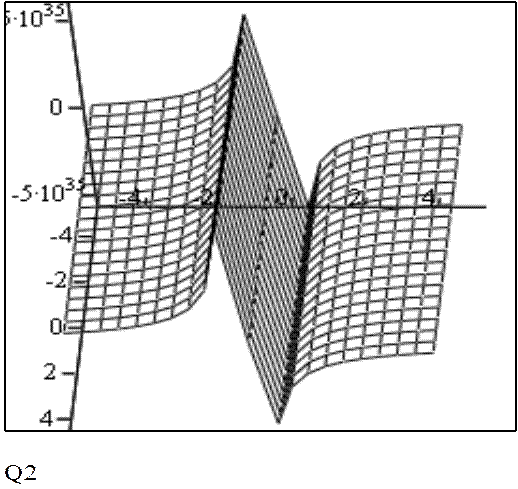
При а = 0.003, b = 0.003.

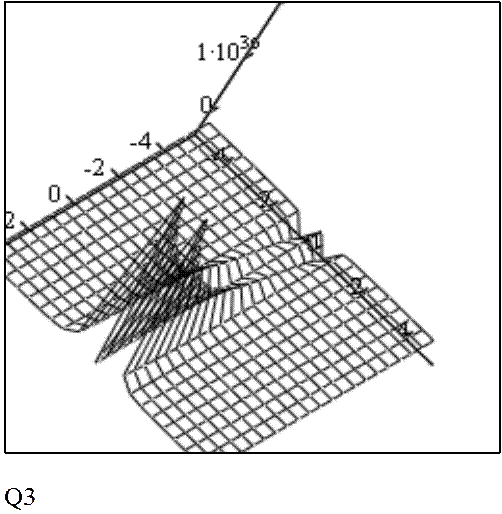
Расчет интегральной передаточной функции. Преобразование Лапласа от интегральной передаточной функции. Построение частотных характеристик. Получение передаточной функции.

По заданному дифференциальному уравнению объекта получим выражение для передаточной функции в распределенных параметрах. Построим ЛАЧХ, аппроксимируем ее с погрешностью 5%, запишем выражение передаточной функции через типовые звенья.

Изображение по Лапласу от нормирующей функции имеет вид:

 

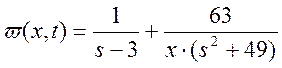
Изображение по Лапласу от входного воздействия:

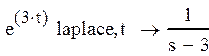
Вынесем в «пролаплашенной» нормирующей функции «пролаплашенное» входное воздействие получим следующее:

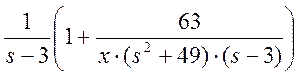
Таким образом, получили следующую функцию:

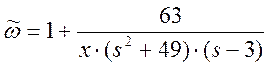
Вычислим интегральную передаточную функцию по формуле:

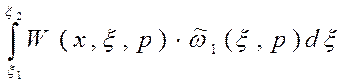
Получим: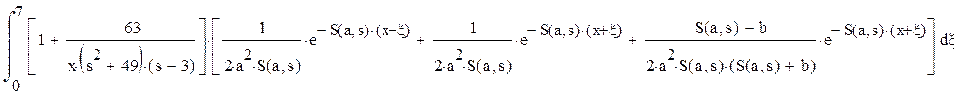

Зафиксировав значение величины х = 10, определим некоторую передаточную функцию. Но, вследствие того, что формула полученной передаточной функции W(s) имеет большой размер, то здесь отображать ее не будем.

По данной передаточной функции построим графики ЛАЧХ, ЛФЧХ, предварительно заменив p на iw:

Графики ЛАЧХ и ЛФЧХ соответственно:

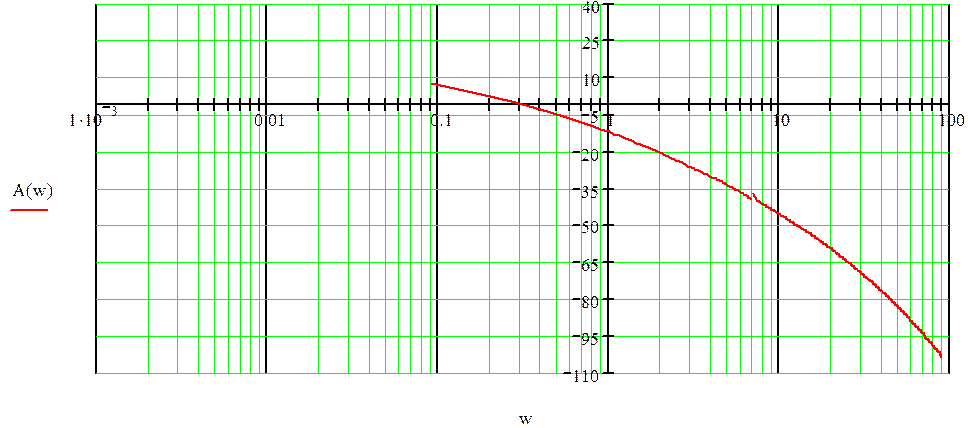
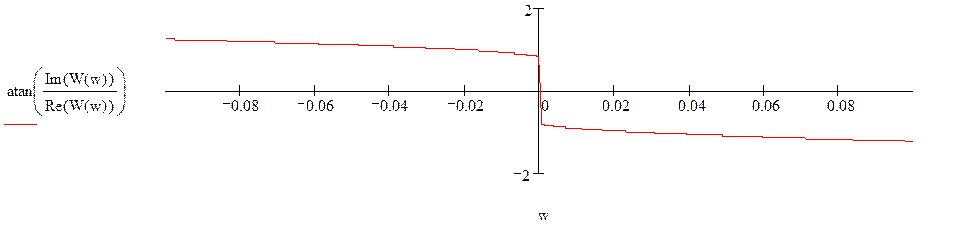
Из графика ЛАЧХ получим данные для записи передаточной функции.

20Log(к)=10 k = 3; w₁=0.1рад/с,  Т₁=2π/w₁=63 c; w₂=7рад/с,  Т₂=2π/w₂=0.9 c

Запишем передаточную функцию

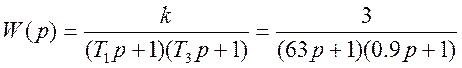
По виду полученной в результате аппроксимации передаточной функции определяем, что система состоит из двух апериодических звеньев первого порядка.