Расчет математической модели на микро- и макроуровне. Расчет математической модели колебания мембраны

ВВЕДЕНИЕ

Первый этап в развитии ТАУ был связан управлением систем, состояние которых характеризуется поведением во времени t некоторого набора конечного числа n-функций одной переменной t. Подобные системы описываются дифференциальными уравнениями (одним или несколькими) относительно Q(t) и называется системой с сосредоточенными параметрами (ССП).

Модели большого числа ОУ могут быть с достаточной для практических целей точности отнесены к классу ССП. Но на практике любой технический ОУ имеет вполне определенные геометрические размеры, поэтому функция, характеризующая его состояние изменяется в пределах пространственной области, занимаемой объектом, а, следовательно, зависит от вектора х в пространственных координатах, являясь функцией Q(x,t) по меньшей мере, двух координат. Если зависимость Q(t) пренебрежительно мала, то такой объект можно отнести к типу ССП. В противном случае этого нельзя сделать без существенных погрешностей в описанных управляющих процессах или даже без потери их качественных особенностей.

Системы, состояния которых описывается функциями нескольких алгоритмов, зависящих как от времени, так и от пространственных координат, получили название СРП.

Моделирование на микроуровне заключается в исследовании систем в распределенных параметрах, а моделирование на макроуровне в построении динамических моделей как систем обыкновенных дифференциальных уравнений.

1  ИСХОДНЫЕ ДАННЫЕ

1) Уравнение колебания круглой трубы:

2) Начальные условия: 3) Граничные условия:                          4) Стандартизирующая функция: 5) Функция Грина: где λn положительные корни уравнения 6) Континуальная передаточная функция:

2 Постановка краевой задачи

Рассмотрим технический объект круглой трубы, длиной lс нулевыми начальными условиями, если на концах струны труба закреплена неподвижно, а с внутренней и внешней поверхности труба испытывает со стороны заделки сопротивление, пропорциональное отклонению и направленное противоположно ему. Внешнее воздействие на трубу описывается плотностью силы g(r,z,t)=0,5·sin(2·t).

Функция Q(r,z,t), описывающая вынужденные колебания трубы определяется уравнением:

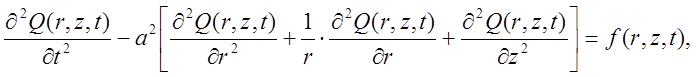
где Q(r,z,t) – отклонение трубы в момент времени t от исходного положения (выходная величина).

f(r,z,t) – управление (возмущение) – входная распределенная величина.

Данное уравнение одномерное гиперболического типа (содержащее вторые производные по времени t и пространственной координаты х).

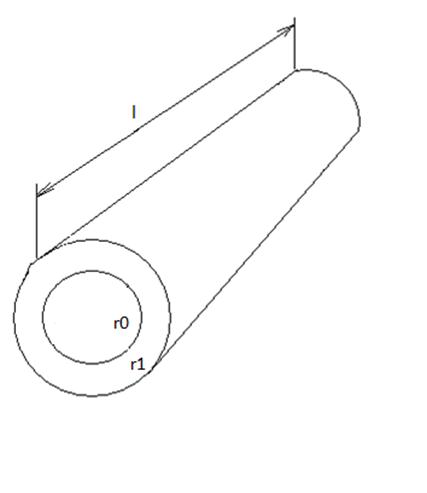
Рисунок 1 – Круглая труба в разрезе

Опишем параметры, входящие в данное уравнение.

Волновая скорость определяется выражением:

,

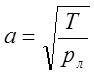где  Т- натяжение, 8 Н;

ρ_л = кг/м³ - линейная плотность (масса, приходящаяся на единицу длины):

ρ_л=ρ∙S=ρ(πR²₁-πR²₀)=0.0381

Задача принимается при условиях:

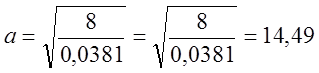
Входное воздействие представим в виде:

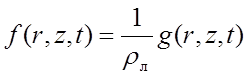
где  - удельная сила;

ρ_л (r,z)=13,123  кг/м – линейная плотность массы трубы (сталь);

g(r,z,t) =0,5·sin(2·t) - линейная плотность продольной внешней силы;

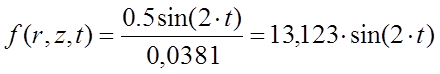
      Построим график по функции

Рисунок 2 –Функция входного воздействия

Примем начальные условия нулевыми:

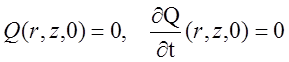
То есть, в начальный момент времени отклонение Q(r,z,t) и его первая производная по всей длине трубы равны 0.

Зададим граничные условия.

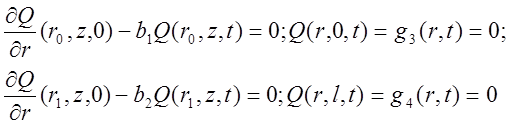
Тогда стандартизирующая функция для данной задачи примет вид:

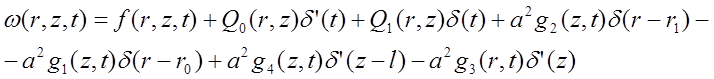
С учетом исходных данных:

 - импульсная функция

2  Расчет выходной величины

Функция Бесселя нулевого порядка определяется последовательными положительными корнями уравнения

Известно ,что b₁ =1,b₂ =1,

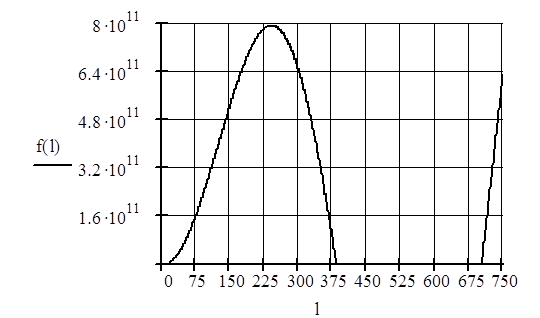
Рисунок 3- Функция Бесселя

Корнями уравнения (10) будут точки пересечения графика с осью λ. Возьмем три первых корня. Из рисунка видно, что они имеют следующие значения

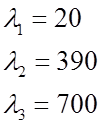
Найдем значения  и для каждого значения λ

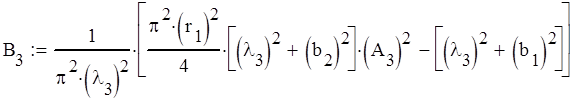
Определим выходную величину данного блока как тройной интеграл по времени и двум пространственным координатам от произведения функции Грина на стандартизирующую функцию. Внутренний интеграл по времени найдем отдельно. Он записывается следующим образом:

,

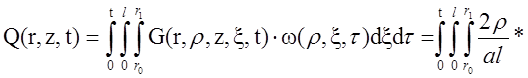
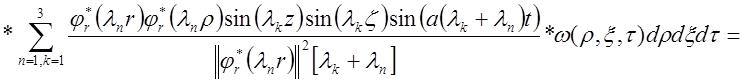
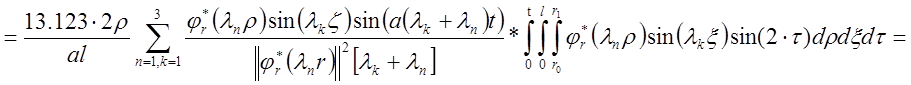
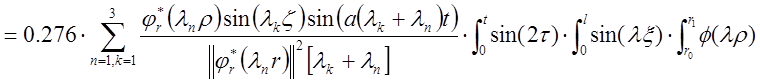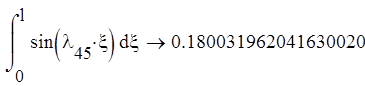
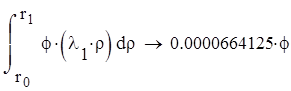
Символьное решение интеграла записывается следующим образом:

Приведем расчет последнего интеграла по радиусу:

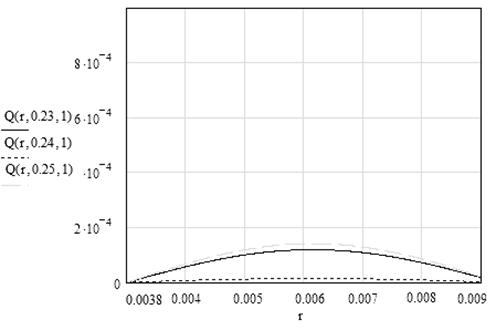
Рисунок 4 – Колебание ствола

4 Расчет динамической характеристики

Динамическая характеристика находится по интегральной передаточной функции, которая рассчитывается как пространственная композиция от произведения континуальной передаточной функции и от преобразованной по Лапласу стандартизирующей функции  с выделенным из нее входным воздействием:

                                                                  

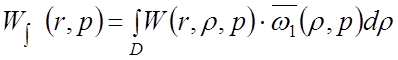
Из нормирующей функции  можно выделить в явном виде через компоненту входной координаты  требуемую :

                                                                                

Поскольку в нашем случае нет возмущающих воздействий, примем =1, тогда =

Найдем изображение стандартизирующей функции по Лапласу:

Тогда

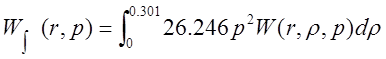
 состоит из трех слагаемых, поэтому разобьем интеграл на три составляющих:

Тогда

Найдем характеристику полученной функции в точке r=0,01:

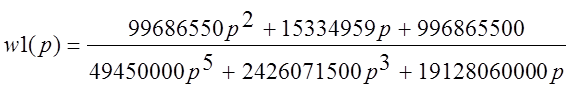
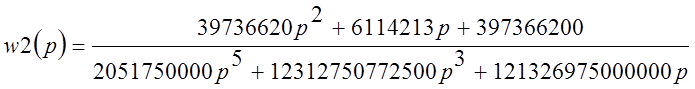
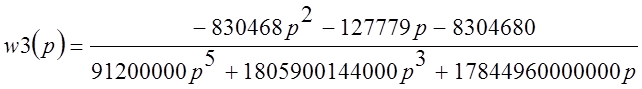
Тогда

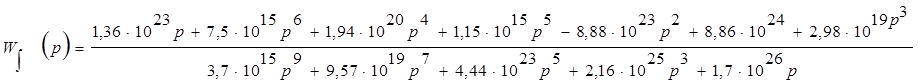
Для выбранной выходной переменной построим ЛАЧХ. При этом необходимо получить частотную форму записи передаточной функции, для этого произведем замену р=jw

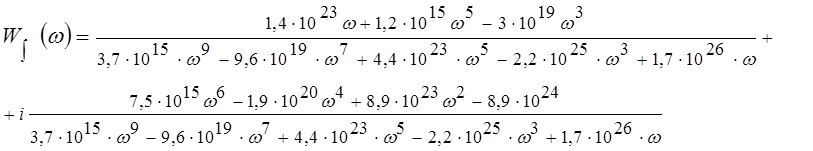
Найдем  ЛАЧХ по выражению:

                                                        

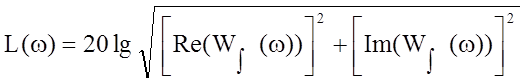
Для построения характеристики используем программу MathCad.

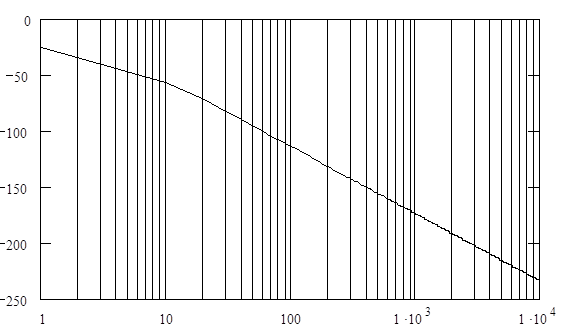
Рисунок 5 – ЛАЧХ

Аппроксимируем ее стандартными типовыми наклонами. Получаем интегрирующее и апериодическое звено с собственной частотой ω=10 Гц. Тогда передаточная функция имеет вид:

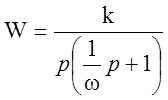
Из ЛАЧХ можно сделать вывод, что усиление равно:

20lgk= – 25.7    k=0.05                                                                                 

С помощью аппроксимации передаточная функция запишется в виде:

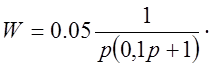
ЗАКЛЮЧЕНИЕ

В данной курсовой работе был произведен расчет математической модели на микро и макроуровне. При моделировании на микроуровне был произведен расчет математической модели колебания мембраны. В ходе расчета была произведена идентификация краевой задачи, расчёт выходной распределенной величины, расчёт динамической характеристики, построен график ЛАЧХ и определена передаточная функция по аппроксимированной ЛАЧХ. При моделировании на макроуровне был были построены графические формы математической модели гидравлической системы, произведен расчет ее параметров, рассчитаны узловой метод формирования математической модели, метод Ньютона для анализа статической модели технической системы, метод Эйлера для анализа динамической модели.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1.  Анисимов И. В. Основы автоматического управления технологическими прцессами химической прмышленности. Л., Химия, 1967. 408с.

2.  Баранов В.Я. Промышленные приборы и средства автоматизации. Справочник, 1987.

3.  Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. М., Наука, 1975. 767с.

4.  Жарковский Б.И. Приборы автоматического контроля и регулирования: учебник для ПТУ. - М.: Высшая школа, 1989. - 450с.

5.  Иващенко Н. Н. Автоматическое регулирование. М., Машиностроение, 1978. 735с.

ПРИЛОЖЕНИЕ А

(обязательное)

Графическая часть

                          1 Исходные данные и идентификация краевой задачи 17     

2 Расчёт статической характеристики                                  18     

                          3 Расчёт динамической характеристики                              19