Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 7

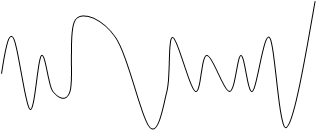
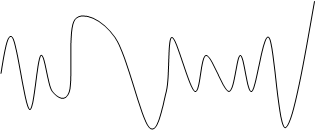
Любой случайный процесс можно разложить в ряд Фурье и представить в виде суммы синусоидальных составляющих различных частот. Говорят: случайный процесс(любой сигнал) можно разложить на гармонические составляющие или представить случайный процесс (временной ряд) в виде  суммы гармонических составляющих. График функции x(t) является суммой трех гармонических составляющих:

x₁(t)-низкочастотные; x₂(t)-среднечастотные; x₃(t)-высокочастотные.

x(t)= x₁(t)+x₂(t)+x₃(t)- определим дисперсию сигнала х:

σ_х²=σ_х1²+ σ_х2²+ σ_х3² т.к. дисперсия суммы равна сумме дисперсий.

х₁→ σ_х1² низкая частота ω₁=2π f₁

х₂→ σ_х2² средняя частота ω₂=2π f₂

х₃→ σ_х3² высокая частота ω₃=2π f₃     ω₃ >ω₂ >ω₁

Построим график, показывающий дисперсию каждого гармонического составляющего. Мы получили разложение

дисперсии случайного процесса, по частоте.

Площадь является общей дисперсией случайного               σ_х1²                 σ_х3²

процесса. Разложение дисперсии случайного                                                                                                           σ_х2²

процесса по частотам гармонических                                                                 S(ω)

составляющих называется спектральная плотность.

                                            σ = ₀∫^∞ S(ω) dω

где S(ω)- спектральная плотность.                                        ω₃       ω₂          ω₁

 

р/м случайный процесс x(t) со средним х                                         _об.

х₀=х- х—центрированная случайная величина    х₀=х- х  = у

              Σ(х-х)²              Σу²

    σ_х²=     Ν-1        =      Ν-1

т.е. дисперсия характеризует средний квадрат случайной величины, который является характеристикой мощности случайного процесса, т.о. спектральная плотность показывает распределение мощности по частоте.

       x(t)                                                          x(t)

                             x

                                                     x                                                     t

                                                                                                                x = x

                                                     t

Корреляционная функция.                                              x₁(t)

Р/м случайные процессы x₁(t), x₂(t), x₃(t).

Они отличаются спектральными составляющими

x₁(t)- низкочастотный

x₂(t)- среднечастотный

x₃(t)-высокочастотный

р/м эти сигналы с другой точки зрения: с точки                                                            t

зрения возможности прогноза случайной величины     x₂(t)

на какой то отрезок времени τ. Низкочастотный

случайный процесс может прогнозироваться на

какой то отрезок времени τ₁. Среднечастотный

случайный процесс может прогнозироваться

на отрезке τ₂ <τ₁. Высокочастотный случайный

процесс может прогнозироваться на отрезке τ₃ <τ₂.                                                       t

Говорят: последующие друг за другом точки

случайного процессы функционально связаны               x₃(t)

между собой, причем время корреляции τ₁

низкочастотного процесса больше времени

корреляции τ₂ среднечастотного процесса и τ₃

высокочастотного процесса. Время корреляции

определяется временем затухания (падения до нуля)

автокорреляционной функции, которая                                                                          t

определяется выражением :

                            _N-τ

  R_xx(τ)=1/(T-τ)*Σ x(t)*x(t+τ)  τ=0,1,2…Ν/4   где Ν-количество точек

 τ₁,τ₂,τ₃-время    ¹ затухания (падения)

    R_x1x1(τ)                                   R_x2x2(τ)                                                   R_x3x3(τ)

 

                                                                                                           τ₃

                          τ₁          τ                     τ₂                    τ                                                  τ

S(ω)= _-∞∫^∞ R(τ)*e ^{-j ωτ}  dτ

Т.о. корреляционная функция и спектральная плотность характеризуют скорость изменения сигнала во времени (во временной плоскости, т.е. когда рассматриваются графики изменения сигнала во времени) или спектральной плоскости. Количественной характеристикой во временной плоскости является корреляционная функция, а в  частотной плоскости- спектральная плотность. Спектральная плотность и корреляционная функция функционально связаны между собой уравнением преобразования Фурье. Преобразование Фурье служит для разложения временного графика на частотные составляющие, т.е. по временному графику x(t). Он позволяет получить параметры гармонических составляющих x₁(t), x₂(t), x₃(t) и т.д.

Математическое описание элементов системы управления.

Характеристики элементов системы:

1)  назначение- функции, которые выполняет данный элемент

2)  принцип(механизм работы)-физические явления, заложенные в основу работы элемента.

3)  конструкция

4)  входные и выходные сигналы

5)  преобразование формы сигнала

6)  математическая модель-уравнение, описывающее законы преобразования входного сигнала в выходной

Математические модели могут иметь вид:

                     а) статические характеристика

                     б) динамические характеристики: временные

                                                                              частотные

Основной характеристикой является дифференциальное уравнение, из которого могут быть получены все другие модели

                     в) передаточная функция

Понятие о математической модели- это совокупность уравнений(алгебраических, дифференциальных), описывающих связь выходной величины с входной, или это уравнения( система уравнений) описывающих данный элемент с какой то конкретной точки зрения, т.е. с конкретно указанными входным и выходным сигналами.