Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 5

Р/м диаграмму потребления электроэнергии микрорайона, мы получим случайный процесс, на второй день мы получим кривую отличную от первой, но тенденции изменения( низкочастотные составляющие) сохранятся. Построим на  одном графике 10-20 кривых, мы имеем 10-20 реализаций случайного процесса.

      P

 

                                                                                                          σ

                                                                                                           x±σ

                                                                                                        t

где  σ- диапазон изменения потребления электроэнергии;

       x±σ- закономерность изменения потребления электроэнергии .

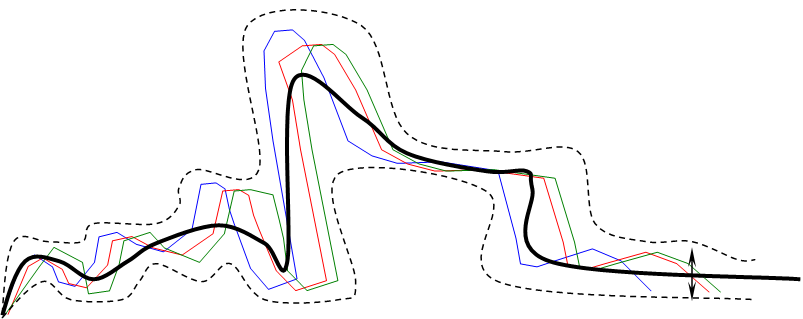
Данное семейство кривых не позволяет точно спрогнозировать значение потребленной энергии, но на данном семействе видны общие закономерности. Полученное семейство позволяет спрогнозировать среднее значение потребляемой энергии (x±σ) и коридор, в пределах которого колеблется случайная величина. Т.о. наилучшим прогнозом является среднее значение х, а ошибка прогноза равна σ, при любом другом значении прогнозируемой величины, величина прогноза увеличивается. Изучая закономерности данного семейства, мы можем добиваться изменения среднего значения и уменьшения коридора изменения случайной величины.

Следовательно, имеются характеристики случайных величин, которые позволяют описывать случайные процессы, прогнозировать их изменение во времени и управлять данными процессами, т.е. целенаправленно формировать закон изменения их во времени.

Например: выводить среднее значение на заданный уровень и добиваться уменьшения ширины колебаний до допустимого значения.

                                                                                                       x(t)

Основные характеристики случайного процесса.

Случайные процессы х₁ и х₂ имеют примерно

одинаковый закон изменения во времени,                                                                          х₁

одинаковые коридоры колебаний, но имеют

разное значение по уровню:

х₁- колеблется вокруг среднего значения х₁

х₂- колеблется вокруг среднего значения х₂

В курсе математики изучали понятие: математическое                                                     х₂

ожидание случайной величины  М.О.( х₁) и М.О.( х₂)- это

теоретическое значение наиболее вероятных значений х₁          t

и х₂, они как правило нам неизвестны и в качестве их

оценок используются среднее значение:

х₁=  ^{Σ х1}                                           х₂=  ^{Σ х2}

        ^{N1                                                                N2}

Например :

1) имеем случайный процесс колебания температуры на уровне 80 ⁰С. Пусть по условиям ведения технологического процесса необходимо уменьшить температуру на 4 ⁰С .

                 T(t)

       80⁰                                                                          T=80⁰  после окончания переходного

                                                                             процесса среднее значение

       76⁰                                                                          T=75⁰  температуры будет равно 76⁰

                                                                 t

2) имеем 2 процесса, в которых температура регулируется на уровне 80⁰ ( Т_задан.=80⁰)

  а) случайная температура колеблется в диапазоне Т₁(t)=80⁰±10⁰

  б)  случайная температура колеблется в диапазоне Т₂(t)=80⁰±5⁰

T₁(t)                                                                T₂(t)

   90⁰                                                                                           85⁰

   80⁰                                                                                          80⁰

  70⁰                                                                 75⁰

                                                             t                                                       t

                            а)                                                                      б)

Процессы различаются шириной коридора колебаний температуры( точностью регулирования). Коридор колебаний(разброс) характеризует дисперсию случайного процесса. Для дисперсии также имеется теоретическое значение. Дисперсия обозначается σ_х1²  и σ_х2². Теоретическое значение часто неизвестно, поэтому пользуются его экспериментальной  оценкой, которая также называется дисперсией и обозначается S_х1²иS_х2²

Σ(х - х_средн. )²

                                                       S²=

                                                                      N-1

Где (N-1)- число степеней свободы.

N-1 на одну единицу меньше чем  N, используемое в формуле расчета среднего, т.к. из и исходного числа степеней свободы N одна степень свободы использована для расчета среднего.

Пример:

дано:  x₁=8       x₂=10       x₃=12

           N=3                                                  x  = (8+10+12)/3=10

Если принято условие, что х среднее равно 10, мы не

можем менять произвольно все исходные данные. Мы

можем изменять любые два значения, выбирая третье

таковым, чтобы среднее значение было равно 10.

ГОВОРЯТ: число степеней свободы уменьшилось с N=3 до N=2.

В формуле дисперсии σ и S- соответственно среднее квадратическое отклонение. Следовательно дисперсия D_x=σ_x². Обратим внимание что х и S_x² (S_x)- расчетные величины, причем х для нас понятная величина (она показывает уровень, вокруг которого колеблется случайная величина).

Р/м связь показатель разброса дисперсии с самим разбросом : х=х±Δ   Δ→ S,S². Для этого р/м третью характеристику случайного процесса- функцию распределения.