Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 6

Случайная величина принимает какое-то значение из коридора ее колебания. Для каждого возможного значения х из данного коридора имеется вероятность принятия случайной величиной данного значения . Зависимость вероятности от значения х называется функция распределения и обозначается f(x).

f(x)- показывает вероятность принятия случайной величиной х конкретного значения из коридора х_min-x_max или х±Δ.

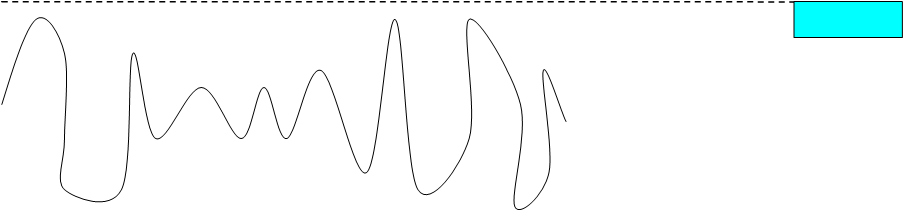
Проведем следующий эксперимент: построим график случайной величины.

1)  найдем  х_min и x_max

2)  разобьем данный коридор на 6 диапазонов.

3)  посчитаем количество значений, попавших в каждый диапазон.

 x(t)

 

                                                                          x_max                                                                                                 n=6

                                                                                                                             n=10

                                                                                                           n=16

                                                                                                           n=14

n=8

n=6

                                                                                  x_min

                                                                                            t

N=Σn=60

Полученный ступенчатый график показывает количество значений, попавших в каждый коридор. Данный график называется гистограмма.

n_i/N- частность. Она показывает относительное значение точек, попавших в данный коридор, и является экспериментальной оценкой вероятности попадания случайной величины в данный коридор, или принятия случайной величиной значения из данного коридора.

Гистограмма-это экспериментальная оценка функции распределения вероятности(f(x)).

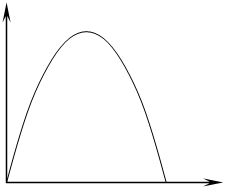
Пусть f(x)            - график теоретической функции распределения, обычно р/м отдельно и изображается в виде:

 

                      1              1-нормальный закон                              3

                                                (колоколообразная кривая)              2

                                     2-равномерное распределение

                                     3-экспоненциальное распределение

                                     4- х²(хи- квадратное распределение)             4

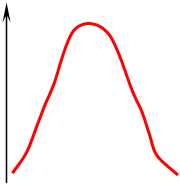
Из определений видно, что первое распределение нормальное, следовательно остальные не нормальные. Нормальное распределение характерно для большого числа случаев.

Вспомним закон больших чисел: если случайная величина зависит от большого числа факторов, примерно различных по влиянию ( практически больше 6 ), то случайная величина имеет нормальный закон распределения.

Обратим внимание: при нормальном законе распределения большое количество случайных значений находится около среднего значения и по мере удаления от среднего это количество уменьшается.                             ₂

                                                                                         e ^{-(x-a) / 2π}

Нормальный закон распределения имеет вид: f(x)= σ   2π  

а- математическое ожидание (оценкой которого является среднее)

σ-среднее квадратическое отклонение

Р/м отличие детерминированной величины от случайной.

Значение детерминированной величины точно определено  в данный момент, и его можно предсказать в будущем.

Значение случайной величины определяется функцией вероятности, т.е., каждое его значение (для непрерывной величины нахождения в каком-то  коридоре) имеет определенную вероятность.

Для нормального закона распределения эти вероятности равны:

1)  х ± σ- находятся 68 % значений                                         х

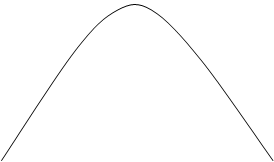
2)  х ± 2σ- находятся 95 % значений

3)  х ± 3σ- находятся 99,7 % значений

 

                                                                                      σ  σ

Фактически случайная величина имеет право быть в диапазонах ± 4σ и ± …σ. При решении технических задач ширину колебаний случайной величины ограничивают, но эти ограничения определяют вероятность (надежность) данного результата. Мы можем сказать, что случайная величина может находиться в диапазоне х ± σ, но надежность  данного результата 68% и т.д. В технических задачах принимают надежность 95%, тогда разброс случайной величины определяется как  х± Δ → х ± 2σ следовательно     Δ = 2σ . При решении задач медицины Δ = 3σ, при решении военных задач Δ = …σ

Правило 3-х σ:

Т.к. диапазон  х ± 3σ включает 99,7 % случайного процесса, то условно считается, что все данные лежат в диапазоне  ± 3σ от среднего.

Дисперсная характеристика определяет ширину коридора разброса случайного процесса. Р/м 2 характеристики : 1) корреляционная функция

                                                    2) спектральная плотность

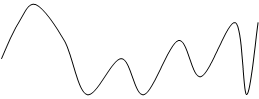
Р/м два графика:

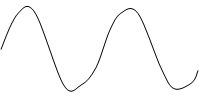
Два случайных процесса x₁(t) и x₂(t) имеют одинаковые среднее и дисперсию, но отличаются скоростью изменения сигнала во времени.

              x₁(t)                                                                 x₂(t)

                                                     t                                                     t

Говорят : данные сигналы отличаются спектральными составляющими, при этом первый сигнал имеет высокочастотные составляющие, а второй низкочастотные.

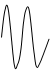
Пример:  x(t)= x₁(t)+x₂(t)+x₃(t)

                                 х₁

х₃

                                                                                                                                    х

              х₂