Принцип работ, функции, алгоритм систем правления с отрицательной обратной связью, страница 4

3)  график функции x(t)=[1(t)-1(t-τ)] t² получается путем умножения ординат графиков функций при различных значениях времени:

           t<0 , то умножают на 0

           t>τ , то умножают на 0                    x(t)

           0≤t≤τ, то умножают на 1

                                                                                   x(t)=[ 1(t)-1(t-τ)] t²

                                                                                                           t

Т.о. 1(t) позволяет включить любую функцию при t=0, 1(t-τ) позволяет включить функцию в момент t=τ, 1(t)-1(t-τ)позволяет включить функцию в момент 0 и отключить в момент τ, т.е. вырезать значения функции на определенном интервале времени. В общем случае ступенчатая функция имеет не нулевое значение, а значение «А», тогда включение ступенчатого сигнала амплитудой А при t=0, описывается уравнением  x(t)=А 1(t).

Импульсное воздействие.

Импульсное воздействие- это сигнал, время действия которого τ относительно мало по сравнению с продолжительностью анализа продолжительности. В зависимости от вида описывающей функции сигнал может быть:

    прямоугольным        трапециидальным      синусоидальным

x₁(t)                               x₂(t)                                x₃(t)

 

                        τ                                  τ                                   τ

                              t                                    t                                   t

Необходимо различать два понятия импульса, импульс как временной сигнал, т.е. закон изменения x(t) (данные сигналы приведены на рисунках), и импульс математический, который равен площади подынтегральной функции временного импульса:     I_x= _-∞∫^∞ x(t) dt.

Введем понятие единичного импульса δ(t)- функция ДИРАКА.

Его свойство: во временной области δ(t)=0 при t≠0, δ(t)=∞ при t=0. Значение импульса такого сигнала (математический импульс) равно 1:

_-∞∫^∞ δ(t) dt=1,

поэтому дельта δ(t) функции Дирака называется: единичный импульсный сигнал.

Она удобна при решении дифференциальных уравнений и анализе работ динамических звеньев.

Напомним: имеется единичная функция хевисайда (во временной плоскости) и единичный импульсный сигнал дельта функция Дирака. Обратим внимание на термин «во временной плоскости»- это означает, что анализируется в плоскости и параметры во времени. По аналогии анализ частотной области - изменение какой-то величины от частоты синусоидального сигнала.   Далее будем рассматривать комплексную область.

     Линейный, квадратичный сигнал.

линейный сигнал:  x₁(t)=at                                        квадратичный сигнал:

                                 x₁^*(t)=l₀+at                                                                        x₂(t)=at²                         

       x(t)                                                                           x(t)

                             x₁^*(t)=l₀+at

                                                                                                           x₂(t)=at²

                             x₁(t)=at

                                                t                                                 t

Обратим внимание: первая производная линейного сигнала равна dx₁/dt =а (a-const), вторая производная  d²x₁/dt² =0. Для квадратичного сигнала - первая производная

dx₂/dt =2аt – линейная функция, вторая производная d²x₂/dt² =2а (2а-const), третья производная d³x₂/dt³ =0. Обратим внимание на то, что сразу мы этого не видим, но, применив наши знания, мы находим эти зависимости.

     Гармонический сигнал.               x(t)                                                    

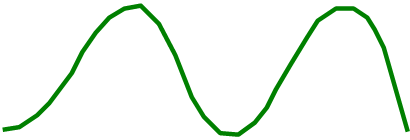
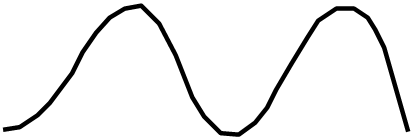
x₁(t)=A sin ωt

x₂(t)=A sin (ωt-φ)

f-частота

ω=2πf- круговая частота

А- амплитуда                                                                                                           t

Т=1/f-период                                           φ                                                                   1    2

Основные понятия синусоидального сигнала рассмотрели выше. Часто анализируется косинусоидальный сигнал x₃(t)=A cos ωt= A sin (ωt+π/2). Обратим внимание: сдвиг по фазе относительно синуса равен π/2 , сдвиг положительный (по оси времени влево).

Случайные сигналы.

Случайные сигналы- это сигналы, которые изменяются во времени случайным образом. Их значение в конкретный момент времени нельзя спрогнозировать, но изучив характеристики случайных сигналов можно прогнозировать уровень случайных сигналов, коридор изменения их во времени и управлять этими характеристиками.

Р/м природу получения случайных сигналов.

Р/м небольшую 2-х комнатную квартиру, в которой имеются следующие потребители электроэнергии: холодильник

                             3 лампы

                             электроплита                 А

Допустим, на входном проводе поставили

амперметр    А   . Запишем диаграмму

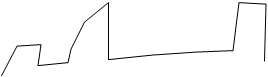
потребления      тока, пусть она имеет вид:

                                                       мы можем четко указать причину каждого изменения

                                                       тока: включили лампочку и холодильник, отключили    

                                                       плиту и т.д. Мы можем прогнозировать график

                                                       потребления энергии. Здесь малое количество

                                                       потребителей и их можно отследить.

Представим, что мы поставим прибор учета на входной кабель подъезда жилого дома. Мы получим случайную кривую, т.к. не сможем связать изменение потребления тока с причинами его изменения.